【数学】2018届一轮复习北师大版任意角的三角函数学案 4页

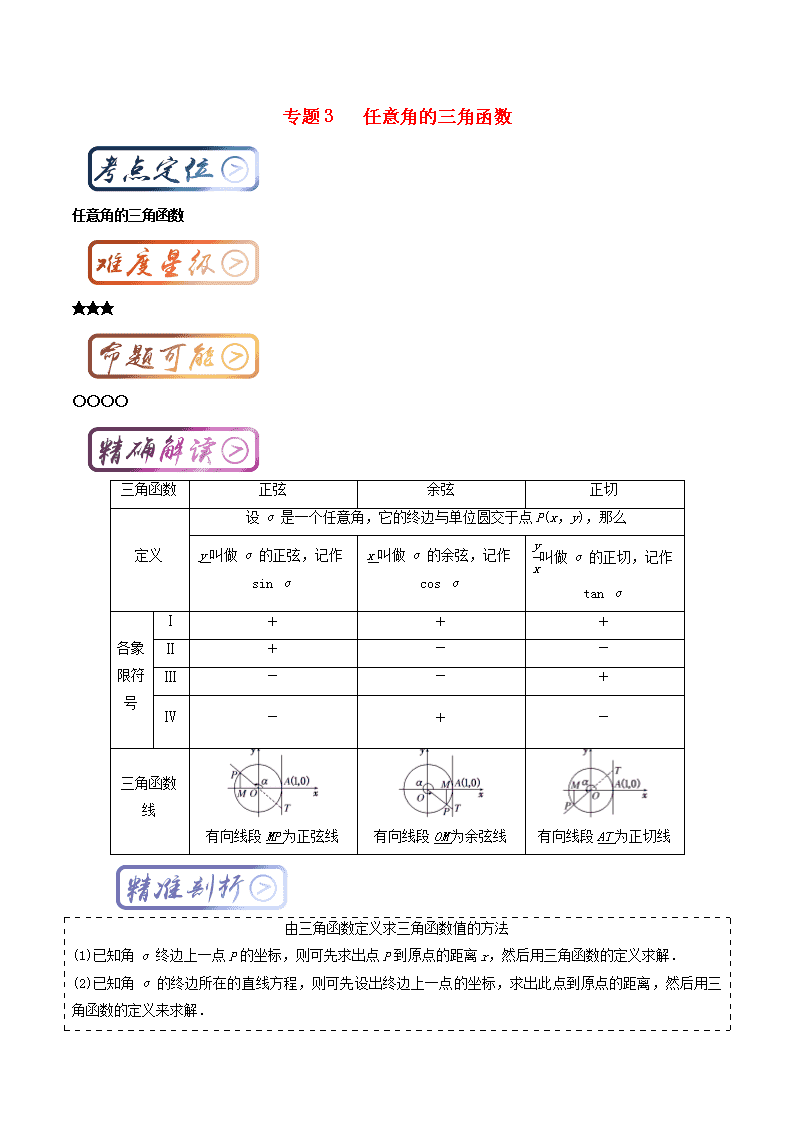
专题3 任意角的三角函数 任意角的三角函数 ‎★★★‎ ‎○○○○‎ 三角函数 正弦 余弦 正切 定义 设α是一个任意角，它的终边与单位圆交于点P(x，y)，那么 y叫做α的正弦，记作sin α x叫做α的余弦，记作cos α 叫做α的正切，记作tan α 各象限符号 Ⅰ ‎＋‎ ‎＋‎ ‎＋‎ Ⅱ ‎＋‎ ‎－‎ ‎－‎ Ⅲ ‎－‎ ‎－‎ ‎＋‎ Ⅳ ‎－‎ ‎＋‎ ‎－‎ 三角函数线 有向线段MP为正弦线 有向线段OM为余弦线 有向线段AT为正切线 由三角函数定义求三角函数值的方法 ‎(1)已知角α终边上一点P的坐标，则可先求出点P到原点的距离r，然后用三角函数的定义求解．‎ ‎(2)已知角α的终边所在的直线方程，则可先设出终边上一点的坐标，求出此点到原点的距离，然后用三角函数的定义来求解．　‎ ‎[例]　(1)已知角α的终边经过点P(4，－3)，则sin α＝________.‎ ‎(2)若角α的终边在直线3x＋4y＝0上，求sin α， cos α和tan α的值．‎ ‎1.若sin αtan α<0，且<0，则角α是(　　)‎ A．第一象限角 B．第二象限角 C．第三象限角 D．第四象限角 ‎[解析]由sin αtan α＜0可知sin α，tan α异号，则α为第二或第三象限角．‎ 由＜0可知cos α，tan α异号，则α为第三或第四象限角．综上可知，α为第三象限角．‎ ‎2.sin 2·cos 3·tan 4的值(　　)‎ A．小于0 B．大于0‎ C．等于0 D．不确定 ‎[解析]　2 rad,3 rad是第二象限角，所以sin 2>0，cos 3<0，4 rad是第三象限角，所以tan 4>0，故sin 2·cos 3·tan 4<0.‎ ‎3.　(1)若角α的终边上有一点P(－4，a)，且sin α·cos α＝，则a的值为(　　)‎ A．4 B．±4 C．－4或－ D. ‎(2)若420°角的终边所在直线上有一点(x,3)，则x的值为________．‎ ‎[解析]　(1)由三角函数的定义得sin α·cos α＝·＝＝，‎ 即a2＋‎16a＋16＝0，‎ 解得a＝－4或－.故选C.‎ ‎(2)由三角函数的定义知tan 420°＝，‎ 所以x＝＝＝.‎ ‎[答案]　(1)C　(2) ‎1.若θ是第二象限角，则下列选项中能确定为正值的是(　　)‎ A．sin B．cos ‎ C．tan D．cos 2θ 解析：选C　由θ是第二象限角可得为第一或第三象限角，所以tan>0，故选C.‎ ‎2.已知θ是第四象限角，则sin(sin θ)(　　)‎ A．大于0 B．大于等于0‎ C．小于0 D．小于等于0‎ 解析：选C　∵θ是第四象限角，∴sin θ∈(－1,0)．令sin θ＝α，当－1<α<0时，sin α<0.故sin(sin θ)<0.‎ ‎3.已知角α的终边与单位圆的交点P，则tan α＝(　　)‎ A. B．± ‎ C. D．± 解析：选B　因为P在单位圆上，所以x2＋2＝1，解得x＝±.所以tan α＝±.‎ ‎4.设α是第二象限角，P(x,4)为其终边上的一点，且cos α＝x，则tan α＝(　　)‎ A. B. ‎ C．－ D．－ 解析：选D　∵α是第二象限角，∴x<0.‎ 又由题意知＝x，‎ 解得x＝－3.‎ ‎∴tan α＝＝－.‎ ‎5.已知角α的终边经过点(‎3a－9，a＋2)，且cos α≤0，sin α＞0，则实数a的取值范围是________．‎ ‎________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________‎