高考数学专题复习课件：7-2 一元二次不等式及其解法 46页

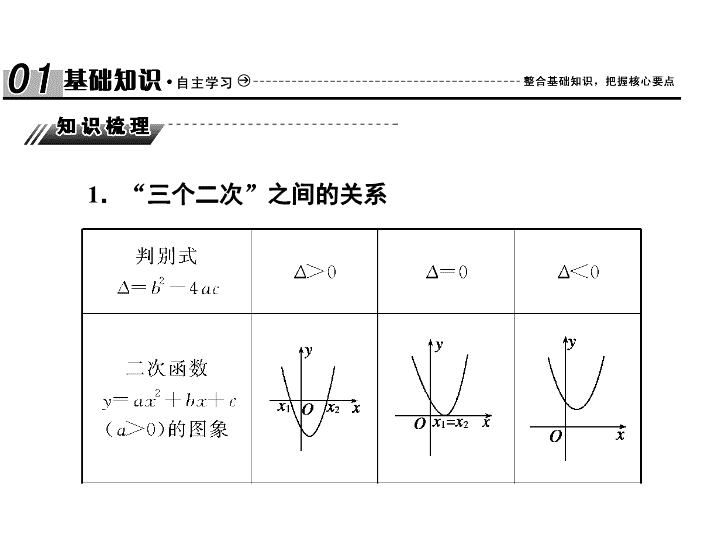
§ 7.2 　一元二次不等式及其解法 [ 考纲要求 ] 　 1. 会从实际情境中抽象出一元二次不等式模型； 2. 通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的关系； 3. 会解一元二次不等式，对给定的一元二次不等式，会设计求解的程序框图． 1 ． “ 三个二次 ” 之间的关系 2. 常用结论 ( x － a )( x － b )>0 或 ( x － a )( x － b )<0 型不等式的解法 口诀：大于取两边，小于取中间． 【 思考辨析 】 　判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) 若不等式 ax 2 ＋ bx ＋ c ＜ 0 的解集为 ( x 1 ， x 2 ) ，则必有 a ＞ 0.( 　　 ) (3) 若不等式 ax 2 ＋ bx ＋ c ＞ 0 的解集是 ( － ∞ ， x 1 ) ∪ ( x 2 ，＋ ∞ ) ，则方程 ax 2 ＋ bx ＋ c ＝ 0 的两个根是 x 1 和 x 2 .( 　　 ) (4) 若方程 ax 2 ＋ bx ＋ c ＝ 0( a ≠ 0) 没有实数根，则不等式 ax 2 ＋ bx ＋ c ＞ 0 的解集为 R.( 　　 ) (5) 不等式 ax 2 ＋ bx ＋ c ≤ 0 在 R 上恒成立的条件是 a ＜ 0 且 Δ ＝ b 2 － 4 ac ≤ 0.( 　　 ) 【 答案 】 (1) √ 　 (2) × 　 (3) √ 　 (4) × 　 (5) × 1 ． ( 教材改编 ) 不等式 x 2 － 3 x － 10 ＞ 0 的解集是 ( 　　 ) A ． ( － 2 ， 5) 　　　　　 B ． (5 ，＋ ∞ ) C ． ( － ∞ ，－ 2) D ． ( － ∞ ，－ 2) ∪ (5 ，＋ ∞ ) 【 解析 】 解方程 x 2 － 3 x － 10 ＝ 0 得 x 1 ＝－ 2 ， x 2 ＝ 5 ， 由 y ＝ x 2 － 3 x － 10 的开口向上，所以 x 2 － 3 x － 10 ＞ 0 的解集为 ( － ∞ ，－ 2) ∪ (5 ，＋ ∞ ) ． 【 答案 】 D 2 ．设集合 M ＝ { x | x 2 － 3 x － 4 ＜ 0} ， N ＝ { x |0 ≤ x ≤ 5} ，则 M ∩ N 等于 ( 　　 ) A ． (0 ， 4] B ． [0 ， 4) C ． [ － 1 ， 0) D ． ( － 1 ， 0] 【 解析 】 ∵ M ＝ { x | x 2 － 3 x － 4 ＜ 0} ＝ { x | － 1 ＜ x ＜ 4} ， ∴ M ∩ N ＝ [0 ， 4) ． 【 答案 】 B 【 答案 】 A 4 ． ( 教材改编 ) 若关于 x 的不等式 m ( x － 1) ＞ x 2 － x 的解集为 { x |1 ＜ x ＜ 2} ，则实数 m 的值为 ________ ． 【 解析 】 因为 m ( x － 1) ＞ x 2 － x 的解集为 { x |1 ＜ x ＜ 2} ． 所以 1 ， 2 一定是 m ( x － 1) ＝ x 2 － x 的解， ∴ m ＝ 2. 【 答案 】 2 5 ． ( 教材改编 ) 若关于 x 的方程 x 2 ＋ ax ＋ a 2 － 1 ＝ 0 有一正根和一负根，则 a 的取值范围为 ________ ． 【 解析 】 由题意可知， Δ ＞ 0 且 x 1 x 2 ＝ a 2 － 1 ＜ 0 ， 故－ 1 ＜ a ＜ 1. 【 答案 】 ( － 1 ， 1) 题型一　一元二次不等式的求解 命题点 1 　不含参的不等式 【 例 1】 求不等式－ 2 x 2 ＋ x ＋ 3 ＜ 0 的解集． 命题点 2 　含参不等式 【 例 2 】 (2016· 青岛模拟 ) 求不等式 12 x 2 － ax ＞ a 2 ( a ∈ R) 的解集． 【 引申探究 】 将原不等式改为 ax 2 － ( a ＋ 1) x ＋ 1 ＜ 0 ，求不等式的解集． 【 方法规律 】 含有参数的不等式的求解，往往需要对参数进行分类讨论． (1) 若二次项系数为常数，首先确定二次项系数是否为正数，再考虑分解因式，对参数进行分类讨论，若不易分解因式，则可依据判别式符号进行分类讨论； (2) 若二次项系数为参数，则应先考虑二次项系数是否为零，确定不等式是不是二次不等式，然后再讨论二次项系数不为零的情形，以便确定解集的形式； (3) 对方程的根进行讨论，比较大小，以便写出解集． 跟踪训练 1 (2016· 河北唐山一模 ) 已知不等式 ax 2 － 3 x ＋ 6 ＞ 4 的解集为 { x | x ＜ 1 或 x ＞ b } ． (1) 求 a ， b ； (2) 解不等式 ax 2 － ( ac ＋ b ) x ＋ bc ＜ 0. 【 解析 】 (1) 因为不等式 ax 2 － 3 x ＋ 6 ＞ 4 的解集为 { x | x ＜ 1 或 x ＞ b } ，所以 x 1 ＝ 1 与 x 2 ＝ b 是方程 ax 2 － 3 x ＋ 2 ＝ 0 的两个实数根，且 b ＞ 1. 由根与系数的关系，得 综上所述，当 c ＞ 2 时，不等式 ax 2 － ( ac ＋ b ) x ＋ bc ＜ 0 的解集为 { x |2 ＜ x ＜ c } ； 当 c ＜ 2 时，不等式 ax 2 － ( ac ＋ b ) x ＋ bc ＜ 0 的解集为 { x | c ＜ x ＜ 2} ； 当 c ＝ 2 时，不等式 ax 2 － ( ac ＋ b ) x ＋ bc ＜ 0 的解集为 ∅ . 题型二　一元二次不等式恒成立问题 命题点 1 　在 R 上恒成立 【 例 3 】 (1) (2016· 江西南昌二中第三次考试 ) 若不等式 ( a － 3) x 2 ＋ 2( a － 3) x － 4 ＜ 0 对一切 x ∈ R 恒成立，则实数 a 取值的集合为 ( 　　 ) A ． ( － ∞ ， 3) 　　　　　　　 B ． ( － 1 ， 3) C ． [ － 1 ， 3] D ． ( － 1 ， 3] 【 答案 】 (1)D 　 (2)[0 ， 1] 命题点 3 　给定参数范围的恒成立问题 【 例 5 】 对任意 m ∈ [ － 1 ， 1] ，函数 f ( x ) ＝ x 2 ＋ ( m － 4) x ＋ 4 － 2 m 的值恒大于零，求 x 的取值范围． 【 解析 】 由 f ( x ) ＝ x 2 ＋ ( m － 4) x ＋ 4 － 2 m ＝ ( x － 2) m ＋ x 2 － 4 x ＋ 4 ， 令 g ( m ) ＝ ( x － 2) m ＋ x 2 － 4 x ＋ 4. 由题意知在 [ － 1 ， 1] 上， g ( m ) 的值恒大于零， 【 方法规律 】 (1) 对于一元二次不等式恒成立问题，恒大于 0 就是相应的二次函数的图象在给定的区间上全部在 x 轴上方，恒小于 0 就是相应的二次函数的图象在给定的区间上全部在 x 轴下方．另外常转化为求二次函数的最值或用分离参数法求最值． (2) 解决恒成立问题一定要搞清谁是主元，谁是参数，一般地，知道谁的范围，谁就是主元，求谁的范围，谁就是参数． 跟踪训练 2 (1) 若不等式 x 2 － 2 x ＋ 5 ≥ a 2 － 3 a 对任意实数 x 恒成立，则实数 a 的取值范围为 ( 　　 ) A ． [ － 1 ， 4] B ． ( － ∞ ，－ 2] ∪ [5 ，＋ ∞ ) C ． ( － ∞ ，－ 1] ∪ [4 ，＋ ∞ ) D ． [ － 2 ， 5] (2) 已知函数 f ( x ) ＝ x 2 ＋ mx － 1 ，若对于任意 x ∈ [ m ， m ＋ 1] ，都有 f ( x ) ＜ 0 成立，则实数 m 的取值范围是 ________ ． 【 解析 】 (1) x 2 － 2 x ＋ 5 ＝ ( x － 1) 2 ＋ 4 的最小值为 4 ， 所以 x 2 － 2 x ＋ 5 ≥ a 2 － 3 a 对任意实数 x 恒成立， 只需 a 2 － 3 a ≤ 4 ，解得－ 1 ≤ a ≤ 4. (2) 作出二次函数 f ( x ) 的草图，对于任意 x ∈ [ m ， m ＋ 1] ， 都有 f ( x ) ＜ 0 ， 【 方法规律 】 求解不等式应用题的四个步骤 (1) 阅读理解，认真审题，把握问题中的关键量，找准不等关系． (2) 引进数学符号，将文字信息转化为符号语言，用不等式表示不等关系，建立相应的数学模型． (3) 解不等式，得出数学结论，要注意数学模型中自变量的实际意义． (4) 回归实际问题，将数学结论还原为实际问题的结果． 跟踪训练 3 某汽车厂上年度生产汽车的投入成本为 10 万元 / 辆，出厂价为 12 万元 / 辆，年销售量为 10 000 辆．本年度为适应市场需求，计划提高产品质量，适度增加投入成本．若每辆车投入成本增加的比例为 x (0 ＜ x ＜ 1) ，则出厂价相应地提高比例为 0.75 x ，同时预计年销售量增加的比例为 0.6 x ，已知年利润＝ ( 出厂价－投入成本 ) × 年销售量． (1) 写出本年度预计的年利润 y 与投入成本增加的比例 x 的关系式； (2) 为使本年度的年利润比上年度有所增加，则投入成本增加的比例 x 应在什么范围内？ 【 思维点拨 】 (1) 考虑 “ 三个二次 ” 间的关系； (2) 将恒成立问题转化为最值问题求解． 即当 x ≥ 1 时， a ＞－ ( x 2 ＋ 2 x ) ＝ g ( x ) 恒成立． 而 g ( x ) ＝－ ( x 2 ＋ 2 x ) ＝－ ( x ＋ 1) 2 ＋ 1 在 [1 ，＋ ∞ ) 上单调递减， ∴ g ( x ) max ＝ g (1) ＝－ 3 ，故 a ＞－ 3. ∴ 实数 a 的取值范围是 { a | a ＞－ 3} ． 【 答案 】 (1)9 　 (2){ a | a ＞－ 3} 【 温馨提醒 】 (1) 本题的解法充分体现了转化与化归思想：函数的值域和不等式的解集转化为 a ， b 满足的条件；不等式恒成立可以分离常数，转化为函数值域问题． (2) 注意函数 f ( x ) 的值域为 [0 ，＋ ∞ ) 与 f ( x ) ≥ 0 的区别 . ► 方法与技巧 1 ． “ 三个二次 ” 的关系是解一元二次不等式的理论基础，一般可把 a ＜ 0 时的情形转化为 a ＞ 0 时的情形． 2 ． f ( x ) ＞ 0 的解集即为函数 y ＝ f ( x ) 的图象在 x 轴上方的点的横坐标的集合，充分利用数形结合思想． 3 ．简单的分式不等式可以等价转化，利用一元二次不等式解法进行求解． ► 失误与防范 1 ．对于不等式 ax 2 ＋ bx ＋ c ＞ 0 ，求解时不要忘记讨论 a ＝ 0 时的情形． 2 ．当 Δ ＜ 0 时， ax 2 ＋ bx ＋ c ＞ 0( a ≠ 0) 的解集为 R 还是 ∅ ，要注意区别． 3 ．含参数的不等式要注意选好分类标准，避免盲目讨论 .