- 122.83 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
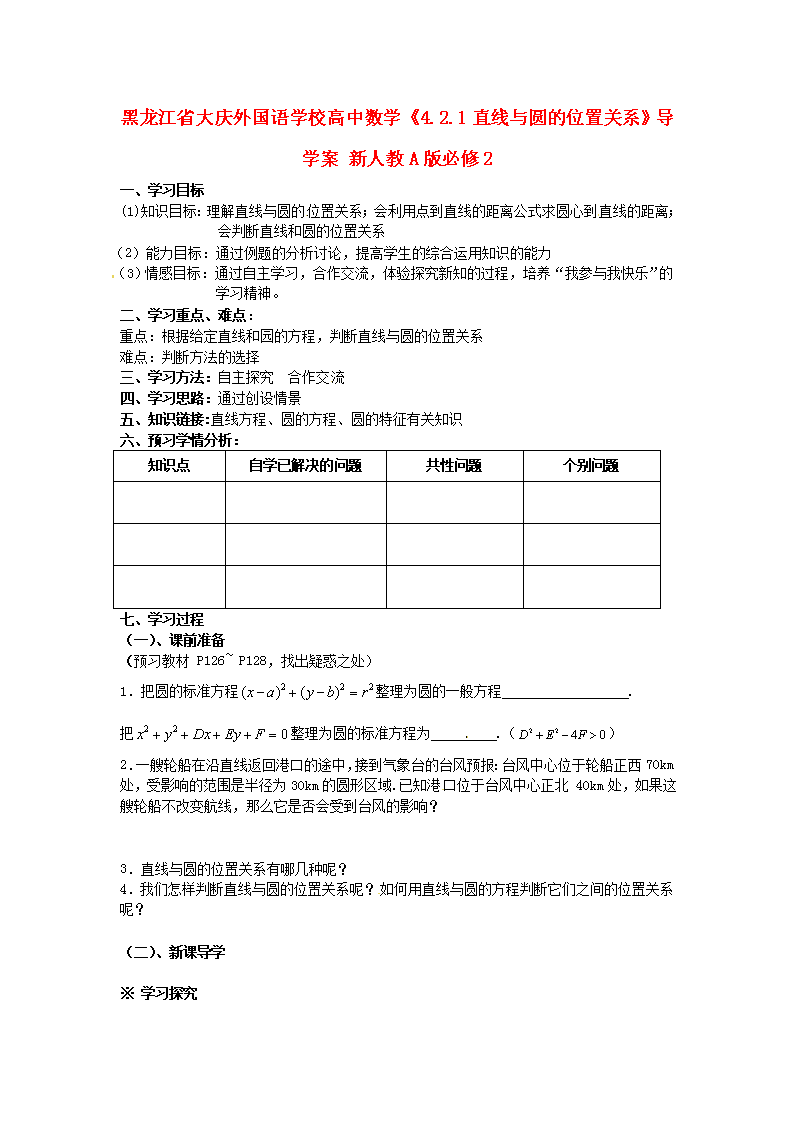
黑龙江省大庆外国语学校高中数学《4.2.1直线与圆的位置关系》导学案 新人教A版必修2
一、学习目标
(1) 知识目标:理解直线与圆的位置关系;会利用点到直线的距离公式求圆心到直线的距离;会判断直线和圆的位置关系
(2)能力目标:通过例题的分析讨论,提高学生的综合运用知识的能力
(3)情感目标:通过自主学习,合作交流,体验探究新知的过程,培养“我参与我快乐”的学习精神。
二、学习重点、难点:
重点:根据给定直线和园的方程,判断直线与圆的位置关系
难点:判断方法的选择
三、学习方法:自主探究 合作交流
四、学习思路:通过创设情景
五、知识链接:直线方程、圆的方程、圆的特征有关知识
六、预习学情分析:
知识点
自学已解决的问题
共性问题
个别问题
七、学习过程
(一)、课前准备
(预习教材 P126~ P128,找出疑惑之处)
1.把圆的标准方程整理为圆的一般方程 .
把整理为圆的标准方程为 .()
2.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径为30km的圆形区域.已知港口位于台风中心正北 40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
3.直线与圆的位置关系有哪几种呢?
4.我们怎样判断直线与圆的位置关系呢?如何用直线与圆的方程判断它们之间的位置关系呢?
(二)、新课导学
※ 学习探究
新知1:设直线的方程为,圆的方程为
圆的半径为 ,圆心到直线的距离为 , 则判别直线与圆的位置关系的依据有以下几点:
⑴当时,直线 与圆相离;
⑵当时,直线 与圆相切;
⑶当时,直线 与圆相交;
新知 2:如果直线的方程为,圆的方程为,将直线方程代入圆的方程,消去得到的一元二次方程式,那么:
⑴当时,直线与圆没有公共点;
⑵当时,直线与圆有且只有一个公共点;
⑶当时,直线与圆有两个不同的公共点;
※ 典型例题
例1 用两种方法来判断直线与圆的位置关系.
例2 如图 ,已知直线过点且和圆相交,截得弦长为 ,求的方程
变式:求直线截圆所得的弦长.
※ 动手试试
练 1. 直线与圆相切,求的值.
例3、例4、
(三)、总结提升
※ 学习小结
判断直线与圆的位置关系有两种方法
① 判断直线与圆的方程组是否有解
a.有解,直线与圆有公共点.有一组则相切?有两组,则相交 ;b. 无解,则直线与圆相离
② 如果直线的方程为,圆的方程为则圆心到直线的距离.
⑴如果时,直线与圆相离;
⑵如果时,直线与圆相切;
⑶如果时,直线与圆相交;
八、学习评价
※ 自我评价 你完成本节导学案的情况为 ( ).
A. 很好 B. 较好 C. 一般 D. 较差
※ 自我检测(时量:5分钟 满分:10分)计分:
1. 直线与圆 ( )
A.相切 B.相离 C.过圆心 D.相交不过圆心
3 已 知 直 线过 点 (- 2,0) , 当 直 线与圆有两个交点时,其斜率的取值范围是( ).
A. B. C. D.
4. 过点的圆的切线方程为 .
5. 圆上的点到直线的距离的最大值为 .
九、课后作业
1.求圆上到直线的距离为的点的坐标.
2. 若直线与圆⑴相交;⑵相切;⑶相离;分别求实数 的
取值范围.
相关文档
- 2019-2020学年陕西省榆林市高一上2021-06-1612页
- 四川省成都外国语学校2021届高三第2021-06-166页
- 重庆市经开礼嘉中学2020届高三下学2021-06-1611页
- 2018年湖北省黄冈市高考数学模拟试2021-06-1612页
- 2014年高考数学(文科)真题分类汇编N2021-06-169页
- 2019年高考数学练习题汇总(三)坐标2021-06-162页
- 【数学】2020届一轮复习人教版(理)第2021-06-1615页
- 【数学】四川省泸县第二中学2019-22021-06-1611页
- 上海市闵行区七宝中学2020届高三上2021-06-1620页
- 【数学】2018届一轮复习人教A版集2021-06-165页