2018年湖北省黄冈市高考数学模拟试卷（理科）（3月份） 12页

‎2018年湖北省黄冈市高考数学模拟试卷（理科）（3月份）‎ 一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎ ‎ ‎1. 设集合P={3, log‎2‎a}‎，Q={a, b}‎，若P∩Q={0}‎，则P∪Q=(‎ ‎)‎ ‎ A.‎{3, 0}‎ B.‎{3, 0, 1}‎ C.‎{3, 0, 2}‎ D.‎‎{3, 0, 1, 2}‎ ‎ ‎ ‎2. 设复数‎3‎‎−‎i‎2017‎在复平面内对应的点为A，过原点和点A的直线的倾斜角为（ ） ‎ A.π‎6‎ B.‎−‎π‎6‎ C.‎2‎‎3‎π D.‎‎5‎‎6‎π ‎ ‎ ‎3. 已知数列‎{an}‎是等差数列，m，p，q为正整数，则“p+q=2m”是“ap‎+aq=2‎am”的（ ） ‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎ ‎ ‎ ‎4. 对任意非零实数a，b，若a*b的运算原理如图所示，则‎(log‎​‎‎2‎2‎2‎)*(‎1‎‎8‎)‎​‎‎−‎‎2‎‎3‎=(‎ ‎)‎ ‎ A.‎1‎ B.‎2‎ C.‎3‎ D.‎‎4‎ ‎ ‎ ‎5. 在直角坐标系xOy中，已知三点A(a, 1)‎，B(2, b)‎，C(3, 4)‎，若OA‎→‎与OB‎→‎在OC‎→‎方向上的投影相同，则a‎2‎‎+‎b‎2‎的最小值为（ ） ‎ A.‎2‎ B.‎4‎ C.‎2‎‎5‎ D.‎‎4‎‎25‎ ‎ ‎ ‎6. 若张三每天的工作时间在‎6‎小时至‎9‎小时之间随机均匀分布，则张三连续两天平均工作时间不少于‎7‎小时的概率是（ ） ‎ A.‎2‎‎9‎ B.‎1‎‎3‎ C.‎2‎‎3‎ D.‎‎7‎‎9‎ ‎ ‎ ‎7. 已知命题p：若α // β，a // α，则a // β；命题q：若a // α，a // β，α∩β=b，则a // b，下列是真命题的是（ ） ‎ A.p∧q B.p∨(‎￢q)‎ C.p∧(‎￢q)‎ D.‎(‎￢‎p)∧q ‎ ‎ ‎8. 《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”．一块“堑堵”型石材表示的三视图如图所示．将该石材切削、打磨，加工成若干个相同的球，并使每个球的体积最大，则所剩余料体积为（        ） ‎ A.‎288−48π B.‎288−16π C.‎288−32π D.‎‎288−4π ‎ ‎ ‎9. 已知x，y满足y≥xx+y≤2‎‎2x−y≥m.‎‎ ‎若z=x+2y有最大值‎4‎，则实数m的值为（ ） ‎ A.‎−4‎ B.‎−2‎ C.‎−1‎ D.‎‎1‎ ‎ ‎ ‎10. 若长度为定值‎4‎的线段AB的两端点分别在x轴正半轴和y轴正半轴上移动，P(x, y)‎为‎△OAB的外心轨迹上一点，则x+y的最大值为（ ） ‎ A.‎1‎ B.‎4‎ C.‎2‎ D.‎‎2‎‎2‎ ‎ ‎ ‎11. 设F‎1‎，F‎2‎分别是双曲线C:x‎2‎a‎2‎−y‎2‎b‎2‎=1(a>0, b>0)‎的左、右焦点，P是C的右支上的点，射线PT平分‎∠F‎1‎PF‎2‎，过原点O作PT的平行线交PF‎1‎于点M，若‎|F‎1‎F‎2‎|=5|MP|‎，则C的离心率为（ ） ‎ 第21页 共24页 ◎ 第22页 共24页 A.‎5‎‎2‎ B.‎2‎ C.‎2‎ D.‎‎3‎ ‎ ‎ ‎12. 对于函数f(x)=‎lnxx，下列说法正确的有(        ) ①f(x)‎在x=e处取得极大值‎1‎e；②f(x)‎有两个不同的零点； ③f(2)1‎． ‎ A.‎4‎个 B.‎3‎个 C.‎2‎个 D.‎1‎个 二.填空题：本大题共4小题，每小题5分．‎ ‎ ‎ ‎ 在‎(‎3‎x−‎‎2‎x‎)‎n的二项展开式中，只有第‎5‎项的二项式系数最大，则二项展开式常数项等于________． ‎ ‎ ‎ ‎ （湖北八市‎3‎月联考）在平面直角坐标系xOy，点P(x‎0‎, y‎0‎)‎是单位圆O上第一象限内的点，‎∠xOP=α，若cosα+‎π‎3‎=−‎‎11‎‎13‎，则x‎0‎的值为________． ‎ ‎ ‎ ‎ 已知实数a>0‎，a≠1‎，函数f(x)=ax‎,x<1‎x‎2‎‎+‎4‎x+alnx,x≥1‎ ‎在R上单调递增，则实数a的取值范围是________． ‎ ‎ ‎ ‎ 已知数列‎{an}‎首项a‎1‎‎=1‎，函数f(x)=x‎4‎+an+1‎cos2x−(2an+1)‎有唯一零点，则数列‎{n(an+1)}‎的前n项的和为________． ‎ 三.解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎ ‎ ‎ 函数f(x)=sin(ωx+φ)(ω>0, |φ|<π‎2‎)‎在它的某一个周期内的单调递减区间是‎[‎5π‎12‎, ‎11π‎12‎]‎．将y=f(x)‎的图象先向左平移π‎4‎个单位，再将图象上所有点的横坐标变为原来的‎1‎‎2‎倍（纵坐标不变），所得到的图象对应的函数记为g(x)‎． ‎ ‎（1）求g(x)‎的解析式；‎ ‎ ‎ ‎（2）设‎△ABC的三边a、b、c满足b‎2‎‎=ac，且边b所对角为x，若关于x的方程g(x)=k有两个不同的实数解，求实数k的取值范围．‎ ‎ ‎ ‎ ‎ ‎ ‎ 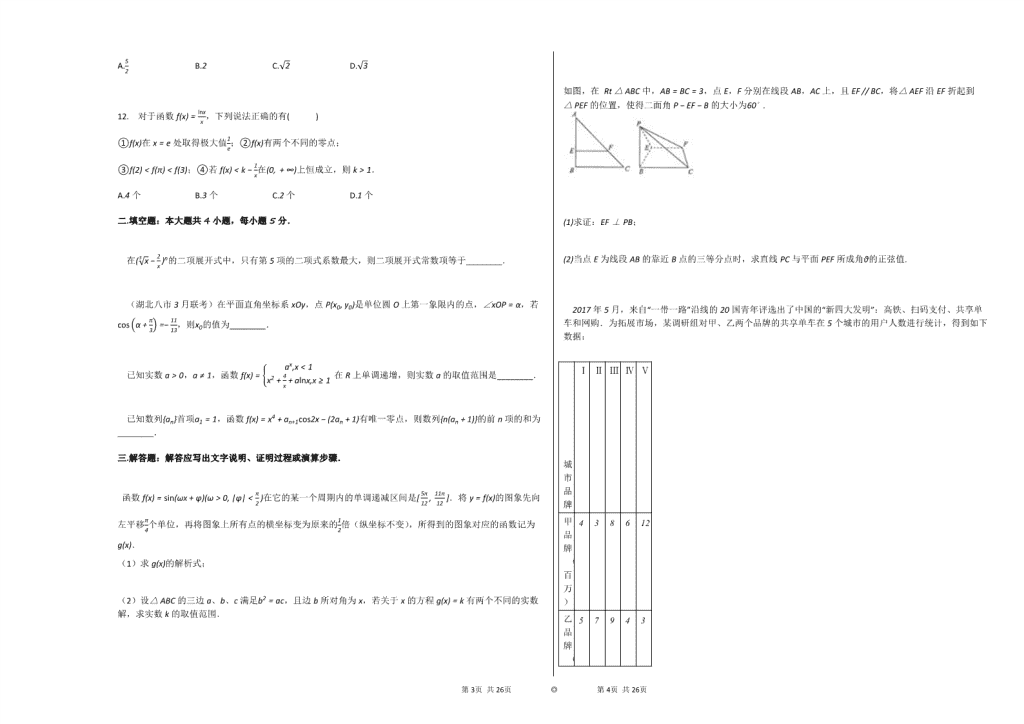如图，在 Rt△ABC中，AB=BC=3‎，点E，F分别在线段AB，AC上，且EF // BC，将‎△AEF沿EF折起到‎△PEF的位置，使得二面角P−EF−B的大小为‎60‎‎∘‎. ‎ ‎ ‎ ‎(1)‎求证：EF⊥PB；‎ ‎ ‎ ‎(2)‎当点E为线段AB的靠近B点的三等分点时，求直线PC与平面PEF所成角θ的正弦值. ‎ ‎ ‎ ‎ ‎2017‎年‎5‎月，来自“一带一路”沿线的‎20‎国青年评选出了中国的“新四大发明”：高铁、扫码支付、共享单车和网购．为拓展市场，某调研组对甲、乙两个品牌的共享单车在‎5‎个城市的用户人数进行统计，得到如下数据： ‎ ‎              城市品牌 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ 甲品牌（百万）‎ ‎4‎ ‎3‎ ‎8‎ ‎6‎ ‎12‎ 乙品牌（百万）‎ ‎5‎ ‎7‎ ‎9‎ ‎4‎ ‎3‎ ‎(‎Ⅰ‎)‎如果共享单车用户人数超过‎5‎百万的城市称为“优质潜力城市”，否则“非优”，请据此判断是否有‎85%‎的把握认为“优质潜力城市”与共享单车品牌有关？ ‎(‎Ⅱ‎)‎如果不考虑其它因素，为拓展市场，甲品牌要从这‎5‎个城市中选出‎3‎个城市进行大规模宣传． ①在城市Ⅰ被选中的条件下，求城市Ⅱ也被选中的概率； ②以X表示选中的城市中用户人数超过‎5‎百万的个数，求随机变量X的分布列及数学期望E(X)‎． 下面临界值表供参考： ‎ P(K‎2‎≥k‎0‎)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k‎0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎ 参考公式：K‎2‎‎=‎n(ad−bc)2‎‎(a+b)(c+d)(a+c)(b+d)‎，‎n=a+b+c+d ‎ ‎ 第21页 共24页 ◎ 第22页 共24页 ‎ 如图，已知抛物线x‎2‎‎=2py(p>0)‎，其焦点到准线的距离为‎2‎，圆S:x‎2‎+y‎2‎−py=0‎，直线l:y=kx+‎p‎2‎与圆和抛物线自左至右顺次交于A，B，C，D四点． ‎ ‎（1）若线段AB，BC，CD的长度按此顺序构成一个等差数列，求正数k的值；‎ ‎ ‎ ‎（2）若直线l‎′‎过抛物线焦点且垂直于直线l，直线l‎′‎与抛物线交于点M，N，设AD，MN的中点分别为Q，P，求证：直线PQ过定点．‎ ‎ ‎ ‎ 已知函数f(x)=‎ex，g(x)=‎‎1‎x−a． ‎ ‎（1）设函数F(x)=f(x)+g(x)‎，试讨论函数F(x)‎零点的个数；‎ ‎ ‎ ‎（2）若a=−2‎，x>0‎，求证：f(x)⋅g(x)>x+1‎+‎x‎2‎‎−8‎‎2x+4‎．‎ ‎[选修4-4：坐标系与参数方程选讲]‎ ‎ ‎ ‎ 在直角坐标系xOy中，曲线C‎1‎参数方程为x=1−‎2‎‎2‎ty=3+‎2‎‎2‎t‎ ‎（t为参数），曲线C‎2‎的参数方程为x=1+cosφy=sinφ‎ ‎（φ为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系． ‎ ‎（1）求曲线C‎1‎，C‎2‎的极坐标方程；‎ ‎ ‎ ‎（2）若射线l:θ=α(ρ>0)‎分别交于C‎1‎，C‎2‎于A，B两点，求‎|OB|‎‎|OA|‎的最大值．‎ ‎[选修4-5：不等式选讲]‎ ‎ ‎ ‎ （1）解关于x的不等式x|x+4|+3<0‎． ‎ ‎（2）关于x的不等式‎|x|+2|x−9|b ‎的值，代入计算可得答案．‎ ‎【解答】‎ 由已知中的程序框图可得，该程序的功能是计算a*b=b−1‎a‎,a≤ba+1‎b‎,a>b ‎的值， 故‎(log‎​‎‎2‎2‎2‎)*(‎1‎‎8‎)‎​‎‎−‎‎2‎‎3‎=3*4=‎4−1‎‎3‎=1‎，‎ ‎5.‎ ‎【答案】‎ D ‎【考点】‎ 平面向量数量积的性质及其运算律 ‎【解析】‎ 由OA‎→‎与OB‎→‎在OC‎→‎方向上的投影相同，可得OA‎→‎‎*OC‎→‎=OB‎→‎*‎OC‎→‎，得到‎3a−4b−2=0‎，再由点到直线的距离公式求解．‎ ‎【解答】‎ ‎∵ 向量OA‎→‎与OB‎→‎在OC‎→‎方向上的投影相同， ∴ OA‎→‎‎*OC‎→‎=OB‎→‎*‎OC‎→‎， ∵ A(a, 1)‎，B(2, b)‎，C(3, 4)‎， ∴ ‎3a+4=6+4b， 即‎3a−4b−2=0‎， ∵ 坐标原点O到直线‎3a−4b−2=0‎的距离为d=‎|−2|‎‎3‎‎3‎‎+(−4‎‎)‎‎2‎=‎‎2‎‎5‎． ∴ a‎2‎‎+‎b‎2‎的最小值为d‎2‎‎=‎‎4‎‎25‎．‎ ‎6.‎ ‎【答案】‎ D ‎【考点】‎ 古典概型及其概率计算公式 ‎【解析】‎ 第21页 共24页 ◎ 第22页 共24页 设张三第一天工作时间为x，第二天工作时间为y，则‎6≤x≤9‎‎6≤y≤9‎x+y‎2‎‎≥7‎‎ ‎，作出可行域，由此能求出张三连续两天平均工作时间不少于‎7‎小时的概率．‎ ‎【解答】‎ 设张三第一天工作时间为x，第二天工作时间为y ∵ 张三每天的工作时间在‎6‎小时至‎9‎小时之间随机均匀分布 张三每天的工作时间不少于‎7‎小时， ∴ ‎6≤x≤9‎‎6≤y≤9‎x+y‎2‎‎≥7‎‎ ‎， 作出可行域，如下图： ∴ 张三连续两天平均工作时间不少于‎7‎小时的概率是： P(A)=S阴SABCD=1−‎1‎‎2‎‎×2×2‎‎3×3‎=‎‎7‎‎9‎．‎ ‎7.‎ ‎【答案】‎ D ‎【考点】‎ 复合命题及其真假判断 ‎【解析】‎ 根据空间直线和平面的位置关系判断两个命题的真假，结合复合命题真假关系进行判断即可．‎ ‎【解答】‎ 若α // β，a // α，则a // β或a⊂β，则命题p是假命题， 若a // α，a // β，α∩β=b，则a // b成立，即命题q是真命题， 则‎(‎￢p)∧q是真命题，其余为假命题，‎ ‎8.‎ ‎【答案】‎ C ‎【考点】‎ 由三视图求体积 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：由三视图知，直三棱柱的底面是直角三角形，直角边分别为‎6‎与‎8‎，要使每个球的体积最大，则球与三个侧面相切．由底面直角三角形内切圆半径为‎2‎，得球的直径为‎4‎．因为棱柱高为‎12‎，所以最多可加工成‎3‎个半径为‎2‎的球，余料的体积为‎1‎‎2‎‎×6×8×12−3×‎4‎‎3‎π×‎2‎‎3‎=288−32π． 故选C．‎ ‎9.‎ ‎【答案】‎ B ‎【考点】‎ 简单线性规划 ‎【解析】‎ 作出不等式组对应的平面区域，利用目标函数的几何意义即可得到结论．‎ ‎【解答】‎ 作出x，y满足y≥xx+y≤2‎‎2x−y≥m.‎‎ ‎对应的平面区域如图： 由图象可知z=x+2y在点A处取得最大值，由x+y=2‎x+2y=4‎‎ ‎， 解得A(0, 2)‎，A在直线‎2x−y=m上， 此时‎0−2=m， 解得m=−2‎，‎ ‎10.‎ ‎【答案】‎ D ‎【考点】‎ 轨迹方程 ‎【解析】‎ 根据线段AB得长度为定值‎4‎，设OA=m，OB=n，根据基本不等式求出mn≤8‎，根据直角三角形的外心所在的位置，表示出x=‎m‎2‎，y=‎n‎2‎，再根据基本不等式即可求出 ‎【解答】‎ 由于线段AB得长度为定值‎4‎， 设OA=m，OB=n， ∴ ‎|AB|=m‎2‎‎+‎n‎2‎=4‎， ∴ ‎16=m‎2‎+n‎2‎≥2mn， ∴ mn≤8‎，当且仅当m=n=2‎‎2‎时取等号， 由于外心是三角形的外接圆的圆心，‎△OAB为直角三角形， 则AB的中点就是外接圆的圆心， ∴ 点P是AB的中点， ∴ x=‎m‎2‎，y=‎n‎2‎， ∴ ‎x+y=‎1‎‎2‎(m+n)≥‎1‎‎2‎×2mn=mn=‎8‎=2‎‎2‎ ‎11.‎ ‎【答案】‎ A ‎【考点】‎ 双曲线的特性 ‎【解析】‎ 运用极限法，设双曲线的右顶点为A，考察特殊情形，当点P→A时，射线PT→‎直线x=a，此时PM→AO，即‎|PM|→a，结合离心率公式即可计算得到．‎ ‎【解答】‎ 第21页 共24页 ◎ 第22页 共24页 设双曲线的右顶点为A， 考察特殊情形，当点P→A时，射线PT→‎直线x=a， 此时PM→AO，即‎|PM|→a， 特别地，当P与A重合时，‎|PM|=a． 由‎|MP|=‎1‎‎5‎|F‎1‎F‎2‎|=‎‎2c‎5‎， 即有a=‎‎2c‎5‎， 由离心率公式e=ca=‎‎5‎‎2‎．‎ ‎12.‎ ‎【答案】‎ B ‎【考点】‎ 利用导数研究函数的极值 ‎【解析】‎ f′(x)=‎‎1−lnxx‎2‎‎，‎(x>0)‎，可得f(x)‎的增区间是‎(0, e)‎，减区间是‎(e, +∞)‎．x=‎‎1‎e时，f(x)‎有极大值f(e)=‎‎1‎e，x→0‎时，f(x)→−∞‎，x→+∞‎时，f(x)→0‎，画出函数f(x)=‎lnxx的图象即可判断①②③． ④，若f(x)lnxx+‎‎1‎x，令G(x)=lnxx+‎‎1‎x，G′(x)=‎‎−lnxx‎2‎，求得G(x)‎的最大值即可．‎ ‎【解答】‎ 解：如图所示， ‎ ‎ f(x)=‎lnxx，‎ ‎∴ f‎′‎‎(x)=‎‎(lnx‎)‎‎′‎x−x‎′‎lnxx‎2‎ ‎=‎‎1−lnxx‎2‎，‎ f(x)‎在‎(0，e)‎上递增，在 ‎(e，+∞)‎ 上递减，‎ ‎∴ f(x)‎在x=e 处有极大值，f(e)=lnee=‎‎1‎e，①正确；‎ ‎∵ x→0‎时， f(x)→−∞,x>e时， f(x)>0‎，‎ ‎∴ f(x)‎在 ‎(0,e)‎ 上有唯一零点，‎ 在‎(e,+∞)‎ 上没有零点，②错误；‎ ‎∵ f(2)−f(π)=ln2‎‎2‎−lnππ=ln‎2‎π−lnπ‎2‎‎2π<0‎, ‎ ‎∴ f(π)>f(2)‎，‎ ‎∵ 函数 f(x)‎在 ‎(e,+∞)‎ 上递减，∴ f(3)>f(π)>f(2)‎ ，③正确;‎ f(x)lnx+1‎x=g(x)‎, ‎ g‎′‎‎(x)=‎−lnxx‎2‎,g(x)‎‎ 在‎(0,1)‎ 上递增，在‎(1,+∞)‎ 上递减， g(x‎)‎max=g(1)=1‎, ∴ k>1‎ ④正确. ∴ 正确的命题个数为‎3‎个. 故选B.‎ 二.填空题：本大题共4小题，每小题5分．‎ ‎【答案】‎ ‎112‎ ‎【考点】‎ 二项式定理的应用 ‎【解析】‎ 由题意可得n=8‎，再利用二项展开式的通项公式，求得二项展开式常数项的值．‎ ‎【解答】‎ ‎(‎3‎x−‎‎2‎x‎)‎n的二项展开式的中，只有第‎5‎项的二项式系数最大，∴ n=8‎， 通项公式为Tr+1‎‎=Cnr⋅(−2‎)‎r⋅xn−4r‎3‎=(−2‎)‎r⋅C‎8‎r⋅‎x‎8−4r‎3‎，令‎8−4r‎3‎‎=0‎，求得r=2‎， 可得二项展开式常数项等于‎4×C‎8‎‎2‎=112‎，‎ ‎【答案】‎ ‎1‎‎26‎ ‎【考点】‎ 三角函数 同角三角函数间的基本关系 两角和与差的余弦公式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 由三角函数的定义，得x‎0‎‎=cosα．因为α∈‎‎0,‎π‎2‎且cos(α+π‎3‎)=−‎‎11‎‎13‎，所以α+π‎3‎∈‎π‎3‎‎,‎‎5π‎6‎，所以sinα+‎π‎3‎=‎‎4‎‎3‎‎13‎，所以x‎0‎‎=cosα=cosα+‎π‎3‎‎−‎π‎3‎=cosα+‎π‎3‎⋅cosπ‎3‎+sinα+‎π‎3‎sinπ‎3‎=−‎11‎‎13‎×‎1‎‎2‎+‎4‎‎3‎‎13‎×‎3‎‎2‎=‎‎1‎‎26‎． 本题考查三角函数的定义、三角恒等变换．‎ ‎【答案】‎ ‎[2, 5]‎ ‎【考点】‎ 分段函数的应用 第21页 共24页 ◎ 第22页 共24页 ‎【解析】‎ 根据题意，对于函数分‎2‎段分析：当x<1‎，f(x)=‎ax，由指数函数的性质分析可得a>1‎①，当x≥1‎，f(x)=x‎2‎+‎4‎x+alnx，由导数与函数单调性的关系可得f′(x)=2x−‎4‎x‎2‎+ax≥0‎在‎[1, +∞)‎上恒成立，变形可得a≥2‎②，再结合函数的单调性，分析可得a≤1+4‎③，联立三个式子，分析可得答案．‎ ‎【解答】‎ 根据题意，函数f(x)=ax‎,x<1‎x‎2‎‎+‎4‎x+alnx,x≥1‎ ‎在R上单调递增， 当x<1‎，f(x)=‎ax，若f(x)‎为增函数，则a>1‎，① 当x≥1‎，f(x)=x‎2‎+‎4‎x+alnx，若f(x)‎为增函数，必有f′(x)=2x−‎4‎x‎2‎+ax≥0‎在‎[1, +∞)‎上恒成立， 变形可得：a≥‎4‎x−2‎x‎2‎， 又由x≥1‎，分析可得‎4‎x‎−2x‎2‎≤2‎， 若a≥‎4‎x−2‎x‎2‎在‎[1, +∞)‎上恒成立，则有a≥2‎，② 若函数f(x)‎在R上单调递增，则有a≤1+4‎，③ 联立①②③可得：‎2≤a≤5‎，‎ ‎【答案】‎ ‎(n−1)⋅‎2‎n+1‎+2‎ ‎【考点】‎ 数列的求和 ‎【解析】‎ f′(x)=4x‎3‎−2an+1‎sin2x‎，由f′(0)=0‎，函数f(x)=x‎4‎+an+1‎cos2x−(2an+1)‎有唯一零点，可得x=0‎是函数f(x)‎的极值点，且f(0)=an+1‎−(2an+1)=0‎， 化为：an+1‎‎+1=2(an+1)‎，a‎1‎‎+1=2‎．利用等比数列的通项公式与求和公式、错位相减法即可得出．‎ ‎【解答】‎ f′(x)=4x‎3‎−2an+1‎sin2x‎， ∵ f′(0)=0‎，函数f(x)=x‎4‎+an+1‎cos2x−(2an+1)‎有唯一零点， ∴ x=0‎是函数f(x)‎的极值点，且f(0)=an+1‎−(2an+1)=0‎， 化为：an+1‎‎+1=2(an+1)‎，a‎1‎‎+1=2‎． ∴ 数列‎{an+1}‎是等比数列，首项与公比都为‎2‎． ∴ an‎+1=‎‎2‎n， ∴ n(an+1)=n⋅‎‎2‎n． ∴ 数列‎{n(an+1)}‎的前n项的和Sn‎=2+2×‎2‎‎2‎+3×‎2‎‎3‎+‎……‎+n⋅‎‎2‎n， ‎2Sn=‎2‎‎2‎+2×‎2‎‎3‎+‎……‎+(n−1)⋅‎2‎n+n⋅‎‎2‎n+1‎， ∴ ‎−Sn=2+‎2‎‎2‎+‎……‎+‎2‎n−n⋅‎2‎n+1‎=‎2(‎2‎n−1)‎‎2−1‎−n⋅‎‎2‎n+1‎， 解得Sn‎=(n−1)⋅‎2‎n+1‎+2‎．‎ 三.解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎【答案】‎ 由题意知，f(x)‎的最小正周期为T=2×(‎11π‎12‎−‎5π‎12‎)=π， ∴ ω=‎2πT=2‎， 又f(‎5π‎12‎)=sin(2×‎5π‎12‎+φ)=1‎， ∴ ‎5π‎6‎‎+φ=π‎2‎+2kπ，解得φ=−π‎3‎+2kπ，k∈Z． 又∵ ‎|φ|<‎π‎2‎，∴ φ=−‎π‎3‎， ∴ f(x)‎的解析式为f(x)=sin(2x−π‎3‎)‎． 将y=f(x)‎的图象向左平移π‎4‎个单位， 得y=sin[2(x+π‎4‎)−π‎3‎]=sin(2x+π‎6‎)‎的图象， 再将图象上所有点的横坐标变为原来的‎1‎‎2‎倍（纵坐标不变）， 得y=sin(4x+π‎6‎)‎， 即g(x)=sin(4x+π‎6‎)‎；‎ ‎△ABC中，b‎2‎‎=ac，且边b所对的角为x， 由余弦定理得：cosx=a‎2‎‎+c‎2‎‎−b‎2‎‎2ac=a‎2‎‎+c‎2‎‎−ac‎2ac≥‎2ac−ac‎2ac=‎‎1‎‎2‎， ∴ ‎00‎，‎∴ k=‎‎2‎‎2‎．‎ ‎（2）证明：由（1）及题意可知Q‎2k,2k‎2‎+1‎， 当k=0‎时，直线l‎′‎与抛物线仅有一个交点，不合题意，所以k≠0‎， 用‎−‎‎1‎k替换k，可得P‎−‎2‎k,‎‎2+‎k‎2‎k‎2‎，‎∴ kPQ=‎k‎2‎‎−1‎k， ‎∴ ‎直线PQ的方程为y−(2k‎2‎+1)=k‎2‎‎−1‎k(x−2k)‎， 化简整理得y=k‎2‎‎−1‎kx+3‎，‎∴ ‎直线PQ过定点‎(0,3)‎．‎ ‎【考点】‎ 抛物线的求解 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ ‎（1）解：由焦点到准线的距离为‎2‎，可得p=2‎， ‎∴ ‎圆S的圆心为S‎0,1‎，半径为‎1‎，因此‎|BC|=2‎， 设Ax‎1‎‎,‎y‎1‎，Dx‎2‎‎,‎y‎2‎，由x‎2‎‎=4y，‎y=kx+1‎ 得x‎2‎‎−4kx−4=0‎， ‎∴ x‎1‎+x‎2‎=4k，x‎1‎x‎2‎‎=−4‎，‎∴ |AD|=‎1+‎k‎2‎|x‎1‎−x‎2‎|=4k‎2‎+4‎， 由图可得‎|AB|+|CD|=|AD|−|BC|=4k‎2‎+4−2=4k‎2‎+2‎， ‎∵ ‎线段AB，BC，CD的长按此顺序构成一个等差数列， ‎∴ |AB|+|CD|=2|BC|=4‎， ‎∴ 4k‎2‎+2=4‎，又‎∵ k>0‎，‎∴ k=‎‎2‎‎2‎．‎ 第21页 共24页 ◎ 第22页 共24页 ‎（2）证明：由（1）及题意可知Q‎2k,2k‎2‎+1‎， 当k=0‎时，直线l‎′‎与抛物线仅有一个交点，不合题意，所以k≠0‎， 用‎−‎‎1‎k替换k，可得P‎−‎2‎k,‎‎2+‎k‎2‎k‎2‎，‎∴ kPQ=‎k‎2‎‎−1‎k， ‎∴ ‎直线PQ的方程为y−(2k‎2‎+1)=k‎2‎‎−1‎k(x−2k)‎， 化简整理得y=k‎2‎‎−1‎kx+3‎，‎∴ ‎直线PQ过定点‎(0,3)‎．‎ ‎【答案】‎ 函数F(x)‎的定义域为‎(−∞, a)∪(a, +∞)‎．当x∈(a, +∞)‎时，ex‎>0‎，‎1‎x−a‎>0‎，所以F(x)=ex+‎1‎x−a>0‎． ∴ 即F(x)‎在区间‎(a, +∞)‎上没有零点． 当x∈(−∞, a)‎时，F(x)=ex+‎1‎x−a=‎ex‎(x−a)+1‎x−a， 令h(x)=ex(x−a)+1‎，则 h‎′‎‎(x)=ex(x−a+1)‎，h‎′‎‎(a−1)=0‎， ∴ 当x∈(−∞, a−1)‎时，h‎′‎‎(x)<0‎，h(x)‎是减函数；当x∈(a−1, a)‎时，h‎′‎‎(x)>0‎，h(x)‎是增函数． ∴ h(x)‎在区间‎(−∞, a)‎上的最小值为h(a−1)=1−‎ea−1‎． 显然，当a=1‎时，h(a−1)=0‎，所以x=a−1‎是f(x)‎的唯一的零点； 当a<1‎时，h(a−1)=1−ea−1‎>0‎，所以F(x)‎没有零点； 当a>1‎时，h(a−1)=1−ea−1‎<0‎，所以F(x)‎有两个零点．‎ 若a=−2‎，x>0‎，要证f(x)g(x)>x+1‎+‎x‎2‎‎−8‎‎2x+8‎， 即要证ex‎>(x+2)x+1‎+‎1‎‎2‎x‎2‎−4‎，∵ x+1‎‎(x+2)(x‎2‎+1)+‎1‎‎2‎x‎2‎−4‎． 设M(x)=ex−(x+2)(x‎2‎+1)−‎1‎‎2‎x‎2‎+4=ex−x‎2‎−2x+2‎，则M‎′‎‎(x)=ex−2x−2‎， 令φ(x)=ex−2x−2‎，则φ′(x)=ex−2‎，∴ φ(x)‎在‎(−∞, ln2)‎上单调递减，在‎(ln2, +∞)‎上单调递增． ∵ φ(1)=e−4<0‎，φ(2)=e‎2‎−6>0‎， ∴ M‎′‎‎(x)‎在‎(0, +∞)‎上只有一个零点x‎0‎‎(10‎， ∴ ex‎>(x+2)(x‎2‎+1)+‎1‎‎2‎x‎2‎−4‎，又‎1‎‎2‎x+1>‎x+1‎， ∴ ex‎>(x+2)x+1‎+‎1‎‎2‎x‎2‎−4‎， ∴ f(x)⋅g(x)>x+1‎+‎x‎2‎‎−8‎‎2x+4‎．‎ ‎【考点】‎ 函数零点的判定定理 ‎【解析】‎ ‎（1）判断F(x)‎的单调性，计算F(x)‎的极值，得出F(x)‎的零点个数； （2）根据x+1‎‎(x+2)(x‎2‎+1)+‎1‎‎2‎x‎2‎−4‎，得出结论．‎ ‎【解答】‎ 函数F(x)‎的定义域为‎(−∞, a)∪(a, +∞)‎．当x∈(a, +∞)‎时，ex‎>0‎，‎1‎x−a‎>0‎，所以F(x)=ex+‎1‎x−a>0‎． ∴ 即F(x)‎在区间‎(a, +∞)‎上没有零点． 当x∈(−∞, a)‎时，F(x)=ex+‎1‎x−a=‎ex‎(x−a)+1‎x−a， 令h(x)=ex(x−a)+1‎，则 h‎′‎‎(x)=ex(x−a+1)‎，h‎′‎‎(a−1)=0‎， ∴ 当x∈(−∞, a−1)‎时，h‎′‎‎(x)<0‎，h(x)‎是减函数；当x∈(a−1, a)‎时，h‎′‎‎(x)>0‎，h(x)‎是增函数． ∴ h(x)‎在区间‎(−∞, a)‎上的最小值为h(a−1)=1−‎ea−1‎． 显然，当a=1‎时，h(a−1)=0‎，所以x=a−1‎是f(x)‎的唯一的零点； 当a<1‎时，h(a−1)=1−ea−1‎>0‎，所以F(x)‎没有零点； 当a>1‎时，h(a−1)=1−ea−1‎<0‎，所以F(x)‎有两个零点．‎ 若a=−2‎，x>0‎，要证f(x)g(x)>x+1‎+‎x‎2‎‎−8‎‎2x+8‎， 即要证ex‎>(x+2)x+1‎+‎1‎‎2‎x‎2‎−4‎，∵ x+1‎‎(x+2)(x‎2‎+1)+‎1‎‎2‎x‎2‎−4‎． 设M(x)=ex−(x+2)(x‎2‎+1)−‎1‎‎2‎x‎2‎+4=ex−x‎2‎−2x+2‎，则M‎′‎‎(x)=ex−2x−2‎， 令φ(x)=ex−2x−2‎，则φ′(x)=ex−2‎，∴ φ(x)‎在‎(−∞, ln2)‎上单调递减，在‎(ln2, +∞)‎上单调递增． ∵ φ(1)=e−4<0‎，φ(2)=e‎2‎−6>0‎， ∴ M‎′‎‎(x)‎在‎(0, +∞)‎上只有一个零点x‎0‎‎(10‎， ∴ ex‎>(x+2)(x‎2‎+1)+‎1‎‎2‎x‎2‎−4‎，又‎1‎‎2‎x+1>‎x+1‎， ∴ ex‎>(x+2)x+1‎+‎1‎‎2‎x‎2‎−4‎， ∴ f(x)⋅g(x)>x+1‎+‎x‎2‎‎−8‎‎2x+4‎．‎ ‎[选修4-4：坐标系与参数方程选讲]‎ ‎【答案】‎ 曲线C‎1‎参数方程为x=1−‎2‎‎2‎ty=3+‎2‎‎2‎t‎ ‎（t为参数）， 转化为直角坐标方程为：x+y−4=0‎． 转化为极坐标方程为：ρcosθ+ρsinθ−4=0‎． 曲线C‎2‎的参数方程为x=1+cosφy=sinφ‎ ‎（φ为参数）， 转化为直角坐标方程为：‎(x−1‎)‎‎2‎+y‎2‎=1‎， 转化为极坐标方程为：ρ=2cosθ．‎ 第21页 共24页 ◎ 第22页 共24页 射线l:θ=α(ρ>0)‎分别交于C‎1‎，C‎2‎于A，B两点， 则：‎|OA|=ρ‎1‎=‎‎4‎cosα+sinα， ‎|OB|=ρ‎2‎=2cosα， 则：‎|OB|‎‎|OA|‎‎=‎cos‎2‎α+sinαcosα‎2‎， ‎=‎‎1+cos2α+sin2α‎4‎， ‎=‎‎1+‎2‎sin(2α+π‎4‎)‎‎4‎． 所以：‎|OB|‎‎|OA|‎max‎=‎‎1+‎‎2‎‎4‎．‎ ‎【考点】‎ 参数方程与普通方程的互化 ‎【解析】‎ ‎（1）直接把参数方程和极坐标方程与直角坐标方程进行转化． （2）利用三角函数的关系变换和极径求出结果．‎ ‎【解答】‎ 曲线C‎1‎参数方程为x=1−‎2‎‎2‎ty=3+‎2‎‎2‎t‎ ‎（t为参数）， 转化为直角坐标方程为：x+y−4=0‎． 转化为极坐标方程为：ρcosθ+ρsinθ−4=0‎． 曲线C‎2‎的参数方程为x=1+cosφy=sinφ‎ ‎（φ为参数）， 转化为直角坐标方程为：‎(x−1‎)‎‎2‎+y‎2‎=1‎， 转化为极坐标方程为：ρ=2cosθ．‎ 射线l:θ=α(ρ>0)‎分别交于C‎1‎，C‎2‎于A，B两点， 则：‎|OA|=ρ‎1‎=‎‎4‎cosα+sinα， ‎|OB|=ρ‎2‎=2cosα， 则：‎|OB|‎‎|OA|‎‎=‎cos‎2‎α+sinαcosα‎2‎， ‎=‎‎1+cos2α+sin2α‎4‎， ‎=‎‎1+‎2‎sin(2α+π‎4‎)‎‎4‎． 所以：‎|OB|‎‎|OA|‎max‎=‎‎1+‎‎2‎‎4‎．‎ ‎[选修4-5：不等式选讲]‎ ‎【答案】‎ ‎∵ x|x+4|+3<0‎， ∴ x+4<0‎‎−x(x+4)+3<0‎‎ ‎或x+4≥0‎x(x+4)+3<0‎‎ ‎， 解得x<−2−‎‎7‎或‎−39‎．‎ ‎【考点】‎ 绝对值不等式的解法与证明 ‎【解析】‎ ‎（1）通过讨论x的范围，得到关于x的不等式组，解出即可； （2）令f(x)=|x|+2|9−x|‎，求出f(x)‎的最小值，从而求出a的范围即可．‎ ‎【解答】‎ ‎∵ x|x+4|+3<0‎， ∴ x+4<0‎‎−x(x+4)+3<0‎‎ ‎或x+4≥0‎x(x+4)+3<0‎‎ ‎， 解得x<−2−‎‎7‎或‎−39‎．‎ 第21页 共24页 ◎ 第22页 共24页