【数学】2018届一轮复习苏教版4-7正余弦定理应用学案 6页

专题4.7 正余弦定理应用 ‎【考纲解读】‎ 内 容 要 求 备注 A　　‎ B　　‎ C　　‎ 解三角形 正弦定理、余弦定理及其应用 ‎　 　‎ ‎√　　‎ ‎　 　‎ 掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题．‎ ‎【直击考点】‎ 题组一　常识题 ‎1．海上有A，B，C三个小岛，A，B两岛相距5海里，从A岛观测到C和B成45°角，从B岛观测到C和A成75°角，则B，C两岛间的距离是________海里．‎ ‎【解析】易知∠ACB＝60°，由正弦定理＝，得＝，即BC＝5.‎ ‎2．已知△ABC中，AB＝，AC＝，A＝60°，则△ABC的面积为________．‎ ‎【解析】由面积公式得S△ABC＝AB·AC·sin A＝.‎ ‎3． 如图，山脚下有一座小塔AB，在塔底B测得山顶C的仰角为60°，在山顶C测得塔顶A的俯角为45°，已知塔高AB＝‎20 m，则山高CD＝________m.‎ ‎【解析】如图，设CD＝x m，则AE＝(x－20) m，tan 60°＝，所以BD＝＝＝x(m)．在△AEC中，x－20＝x，解得x＝10(3＋)．‎ 题组二　常错题 ‎4．在某次测量中，在A处测得同一半平面方向的B点的仰角是60°，C点的俯角是70°，则∠BAC＝________．‎ ‎【解析】由已知可知∠BAD＝60°，∠CAD＝70°，所以∠BAC＝60°＋70°＝130°.‎ ‎5．若点A在点C的北偏东30°，点B在点C的南偏东60°，且AC＝BC，则点A在点B的方位是____________．‎ 题组三　常考题 ‎6．要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD＝120°，CD＝‎40 m，则电视塔的高度为________．‎ ‎【解析】设电视塔的高度为x m，则BC＝x m，BD＝x m．在△BCD中，由余弦定理，得3x2＝x2＋402－2×40x×cos 120°，即x2－20x－800＝0，解得x＝－20(舍去)或x＝40.‎ ‎7．一船自西向东匀速航行，上午10时到达一座灯塔P的南偏西75°距塔68海里的M处，下午2时到达这座灯塔的东南方向的N处，则这只船的航行速度为________海里/小时．‎ ‎【知识清单】‎ 考点1 正弦定理、余弦定理的实际运用 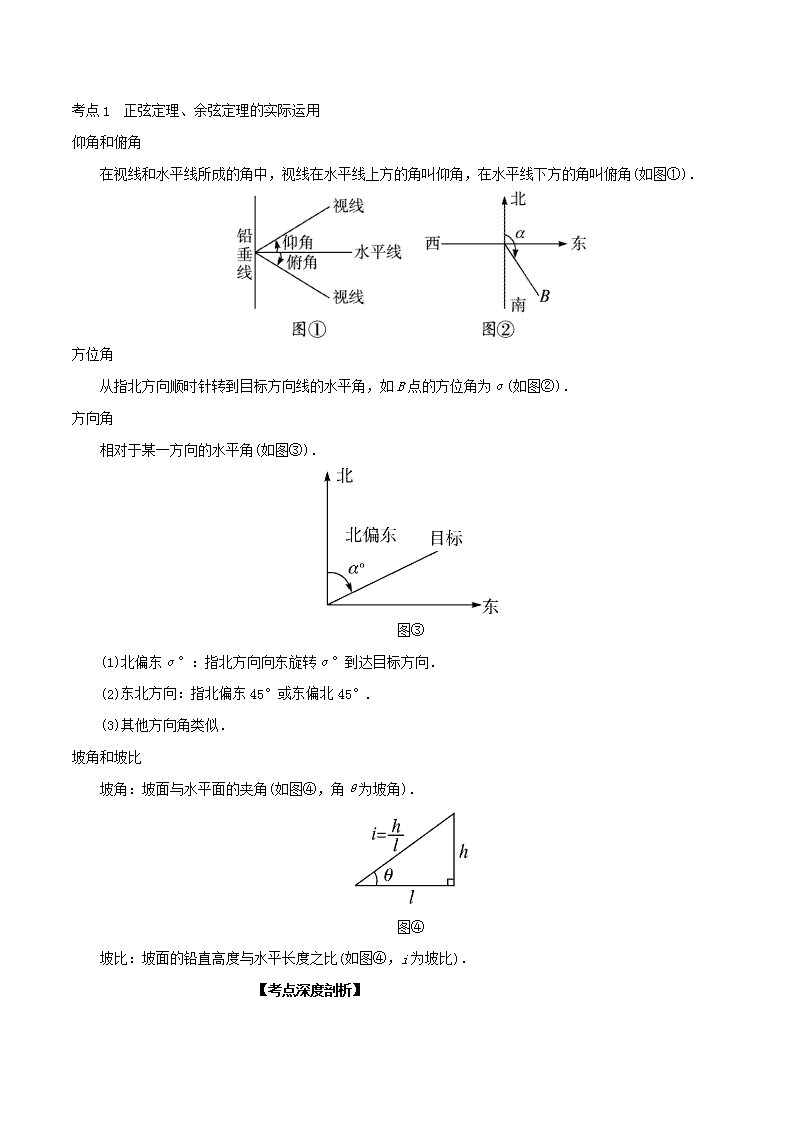仰角和俯角 在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫俯角(如图①)．‎ 方位角 从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α(如图②)．‎ 方向角 相对于某一方向的水平角(如图③)．‎ 图③‎ ‎(1)北偏东α°：指北方向向东旋转α°到达目标方向．‎ ‎(2)东北方向：指北偏东45°或东偏北45°.‎ ‎(3)其他方向角类似．‎ 坡角和坡比 坡角：坡面与水平面的夹角(如图④，角θ为坡角)．‎ 图④‎ 坡比：坡面的铅直高度与水平长度之比(如图④，i为坡比)．‎ ‎【考点深度剖析】‎ ‎ 这类实际应用题，实质就是解三角形问题，一般都离不开正弦定理和余弦定理，在解题中，首先要正确地画出符合题意的示意图，然后将问题转化为三角形问题去求解．注意：①基线的选取要恰当准确；②选取的三角形及正、余弦定理要恰当．‎ ‎【重点难点突破】‎ 考点1 正弦定理、余弦定理的实际运用 ‎【1-1】甲，乙两船同时从点出发，甲以每小时的速度向正东航行，乙船以每小时的速度沿南偏东的方向航行，小时后，甲、乙两船分别到达两点，此时的大小为 ；‎ ‎【答案】‎ 平分BC，∴AB=AC=‎20km，根据余弦定理BC2=AB2+AC2-2AB•AC•cos∠BAC，得：1200=400+400-800cos∠BAC，∴cos∠BAC=- ，又∠BAC为三角形的内角，则∠BAC=120°．故答案为：120°‎ ‎【1-2】某个公园有个池塘，其形状为直角△ABC，‎ ‎∠C=90°，AB=‎2百米，BC=‎1百米．‎ ‎ （Ⅰ）现在准备养一批供游客观赏的鱼，分别在AB、BC、CA上取点D，E，F，如图(1)，使得EF‖AB，EF ‎⊥ED，在△DEF喂食，求△DEF 面积S△DEF的最大值； （Ⅱ）现在准备新建造一个荷塘，分别在AB，BC，CA上取点D，E，F，如图(2)，建造△DEF连廊（不考虑宽度）供游客休憩，且使△DEF为正三角形，求△DEF边长的最小值．‎ ‎ （Ⅱ）设正的边长为，，‎ ‎【思想方法】‎ ‎(1)阅读理解题意，弄清问题的实际背景，明确已知与未知，理清量与量之间的关系．‎ ‎(2)根据题意画出示意图，将实际问题抽象成解三角形问题的模型．‎ ‎(3)根据题意选择正弦定理或余弦定理求解．‎ ‎(4)将三角形问题还原为实际问题，注意实际问题中的有关单位问题、近似计算的要求等．‎ ‎【温馨提醒】测量角度时，要准确理解方位角、方向角的概念，准确画出示意图是关键．‎ ‎【易错试题常警惕】‎ ‎(1)画出示意图后要注意寻找一些特殊三角形，如等边三角形、直角三角形、等腰三角形等，这样可以优化解题过程。‎ ‎(2)解三角形时，为避免误差的积累，应尽可能用已知的数据(原始数据)，少用间接求出的量。‎