- 453.50 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
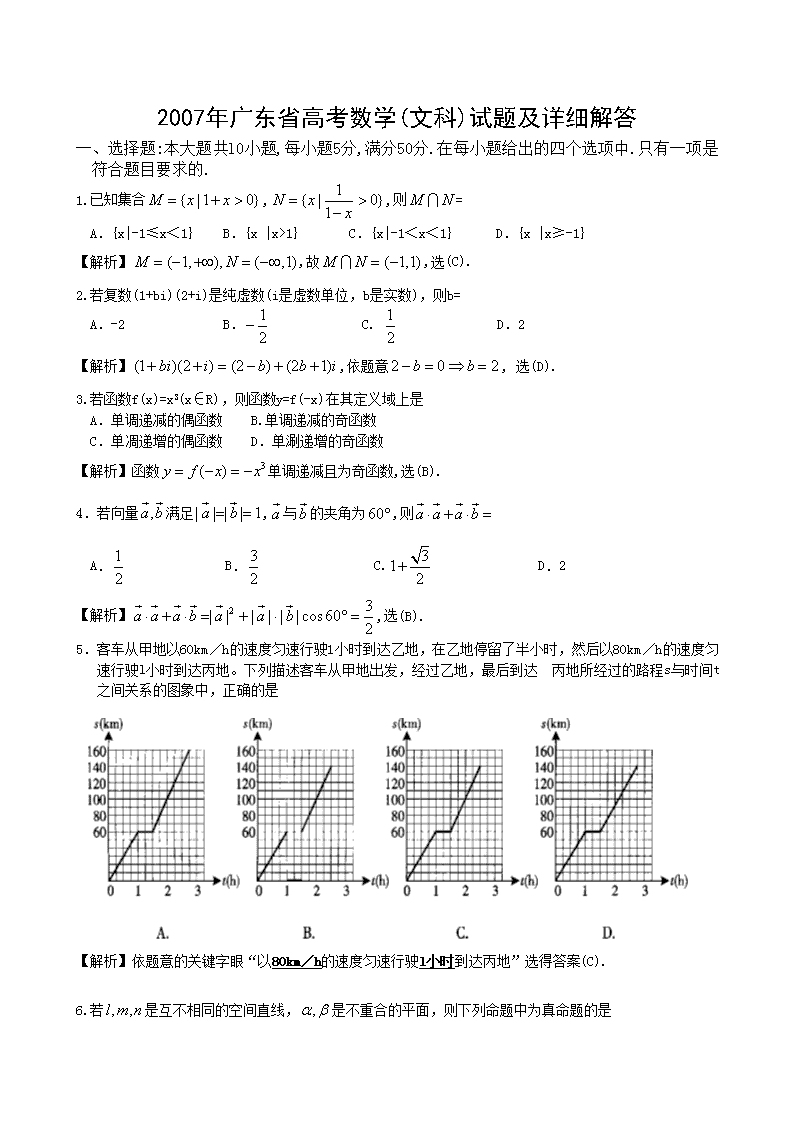
2007年广东省高考数学(文科)试题及详细解答
一、选择题:本大题共l0小题,每小题5分,满分50分.在每小题给出的四个选项中.只有一项是符合题目要求的.
1.已知集合,,则=
A.{x|-1≤x<1} B.{x |x>1} C.{x|-1<x<1} D.{x |x≥-1}
【解析】,故,选(C).
2.若复数(1+bi)(2+i)是纯虚数(i是虚数单位,b是实数),则b=
A.-2 B. C. D.2
【解析】,依题意, 选(D).
3.若函数f(x)=x3(x∈R),则函数y=f(-x)在其定义域上是
A.单调递减的偶函数 B.单调递减的奇函数
C.单凋递增的偶函数 D.单涮递增的奇函数
【解析】函数单调递减且为奇函数,选(B).
4.若向量满足,与的夹角为,则
A. B. C. D.2
【解析】,选(B).
5.客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶l小时到达丙地。下列描述客车从甲地出发,经过乙地,最后到达 丙地所经过的路程s与时间t之间关系的图象中,正确的是
【解析】依题意的关键字眼“以80km/h的速度匀速行驶l小时到达丙地”选得答案(C).
6.若是互不相同的空间直线,是不重合的平面,则下列命题中为真命题的是
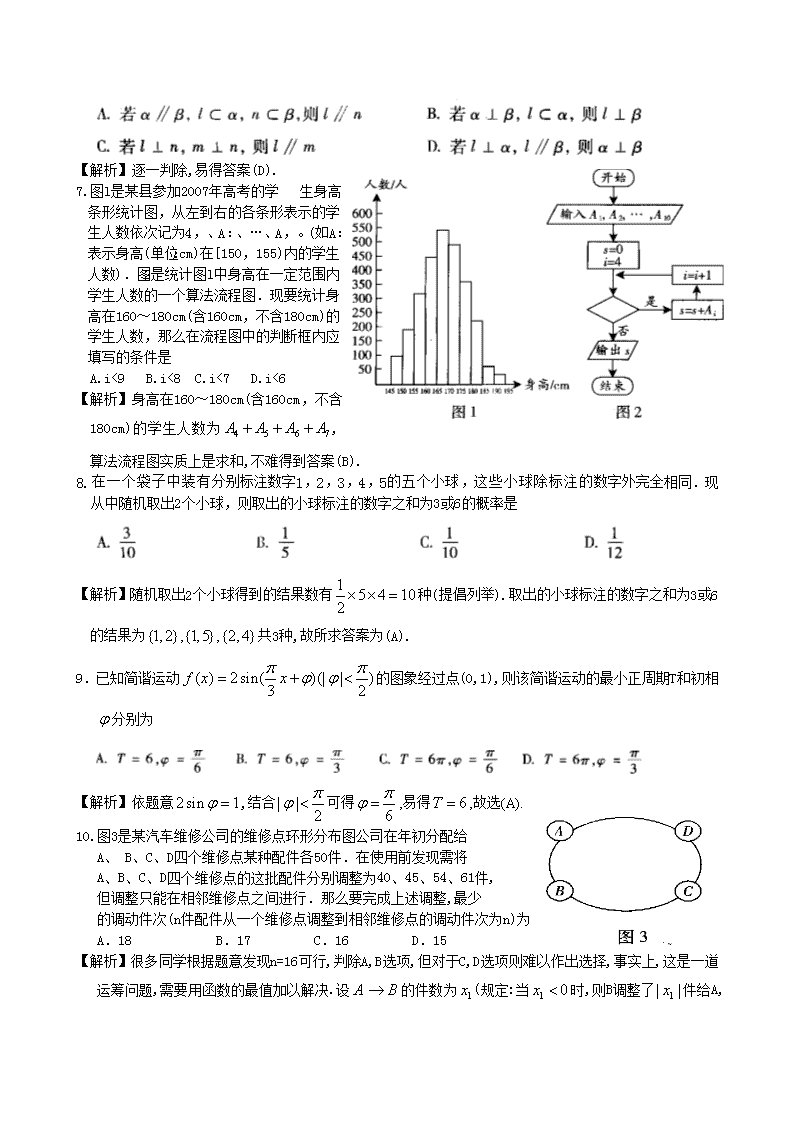
【解析】逐一判除,易得答案(D).
7.图l是某县参加2007年高考的学 生身高条形统计图,从左到右的各条形表示的学生人数依次记为4,、A:、…、A,。(如A:表示身高(单位:cm)在[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是
A.i<9 B.i<8 C.i<7 D.i<6
【解析】身高在160~180cm(含160cm,不含180cm)的学生人数为,算法流程图实质上是求和,不难得到答案(B).
8.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是
【解析】随机取出2个小球得到的结果数有种(提倡列举).取出的小球标注的数字之和为3或6的结果为共3种,故所求答案为(A).
9.已知简谐运动的图象经过点(0,1),则该简谐运动的最小正周期T 和初相分别为
【解析】依题意,结合可得,易得,故选(A).
10.图3是某汽车维修公司的维修点环形分布图公司在年初分配给
A、 B、C、D四个维修点某种配件各50件.在使用前发现需将
A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,
但调整只能在相邻维修点之间进行.那么要完成上述调整,最少
的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为
A.18 B.17 C.16 D.15
【解析】很多同学根据题意发现n=16可行,判除A,B选项,但对于C,D选项则难以作出选择,事实上,这是一道运筹问题,需要用函数的最值加以解决.设的件数为(规定:当时,则B调整了
件给A,下同!),的件数为,的件数为,的件数为,依题意可得,,,,
从而,,,故调动件次,
画出图像(或绝对值的几何意义)可得最小值为16,故选(C).
二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.
11.在平面直角坐标系xOy中,已知抛物线关于x轴对称,顶点在原点O,且过点P(2,4),则该抛物线的方程是 .
【解析】设所求抛物线方程为,依题意,故所求为.
12.函数f(x)=xlnx(x>0)的单调递增区间是 .
【解析】由可得,答案:.
13.已知数列{an}的前n项和Sn=n2-9n,则其通项an= ;若它的第k项满足5β),是的导数,设 (1)求的值;(2)已知对任意的正整数有,记,求数列的前项和.
【解析】(1)求根公式得, …………3分
(2)………4分 ………5分 ……7分
……10分
∴数列是首项,公比为2的等比数列………11分
∴………………………………………………………14分
21.(本小题满分l4分)
已知是实数,函数.如果函数在区间[-1,1]上有零点,求的取值范围.
【解析】若,则,令,不符题意, 故………2分
当在 [-1,1]上有一个零点时,此时或………6分
解得或 …………………………………………………………………8分
当在[-1,1]上有两个零点时,则………………………………10分
解得即………………12分
综上,实数的取值范围为. ……………………………………14分
(别解:,题意转化为知求的值域,
令得转化为勾函数问题.)
相关文档
- 高考文科数学复习:夯基提能作业本 (2021-06-166页
- 人教新课标A版高三数学复习 公式大2021-06-167页
- 人教版必修1高一数学:精品教案(全套2021-06-16150页
- 2016届高考数学(理)大一轮复习达标训2021-06-166页
- 四川省内江市2018-2019学年高一下2021-06-1618页
- 黑龙江省哈尔滨市第一中学2020届高2021-06-167页
- 【数学】2019届一轮复习北师大版概2021-06-1610页
- 高中数学人教a版必修二 模块综合测2021-06-1612页
- 天津市河北区2020届高三高考二模数2021-06-1621页
- 【数学】河北省唐山市第一中学20192021-06-1614页