【数学】2019届一轮复习北师大版 空间中的平行与垂直 学案 26页

‎ ‎ 高考考点 命题分析 三年高考探 ‎ 考查频率 空间点、线、面位置关系的基本问题 空间点、线、面位置关系既是高考的必考点，也是考查的难点，其在高考中的命题形式较为稳定，以解答题的形式重点考查空间平行关系和垂直关系的证明 ‎2016课标全国Ⅱ14‎ ‎★★★[ ]‎ 平行与垂直关系的证明[ ‎ ‎2017课标全国Ⅰ18‎ ‎2016课标全国Ⅲ19‎ ‎2015课标全国Ⅰ18‎ ‎★★★★★‎ 平面图形的翻折与存在性问题 ‎2016课标全国Ⅱ19‎ ‎★★★‎ 考点1 空间点、线、面位置关系的基本问题 题组一 位置关系的判断 调研1 设m,n是两条不同的直线,α,β是两个不同的平面,给出下列四个命题 ‎ ‎①若m∥n,m⊥β,则n⊥β; ②若m∥α,m∥β,则α∥β;‎ ‎③若m∥n,m∥β,则n∥β; ④若m⊥α,m⊥β则α⊥β.‎ 其中真命题的个数为 A．1 B．2‎ C．3 D．4‎ ‎【答案】A ‎【解析】根据空间平行与垂直的判定和性质定理逐个对命题进行判断. ①显然正确;‎ 对于②,由m∥α,m∥β,不一定得到α∥β,α和β的关系不确定;‎ 对于③,n可能在平面β内,所以③不正确;‎ 对于④,由m⊥α,m⊥β,可知α∥β,所以④不正确.‎ 故选A． ‎ ‎☆技巧点拨☆‎ 空间中点、线、面的位置关系的判定方法 ‎ ‎(1)可以从线、面的概念、定理出发， 会找特例、反例．‎ ‎(2)可以借助长方体，在理解空间点、线、面位置关系的基础上，抽象出空间线、面的位置关系的定义．‎ 题组二 位置关系的判断与其他知识相结合 调研2 已知l为平面α内的一条直线，α，β表示两个不同的平面，则“α⊥β ”是“l⊥β ”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【答案】B ‎【解析】若l为平面α内的一条直线且l⊥β，则α⊥β，反过 则不一定成立，所以“α⊥β”是“l⊥β”的必要不充分条件，故选B．‎ 考点2 平行与垂直关系的证明 题组一 平行的判定及性质 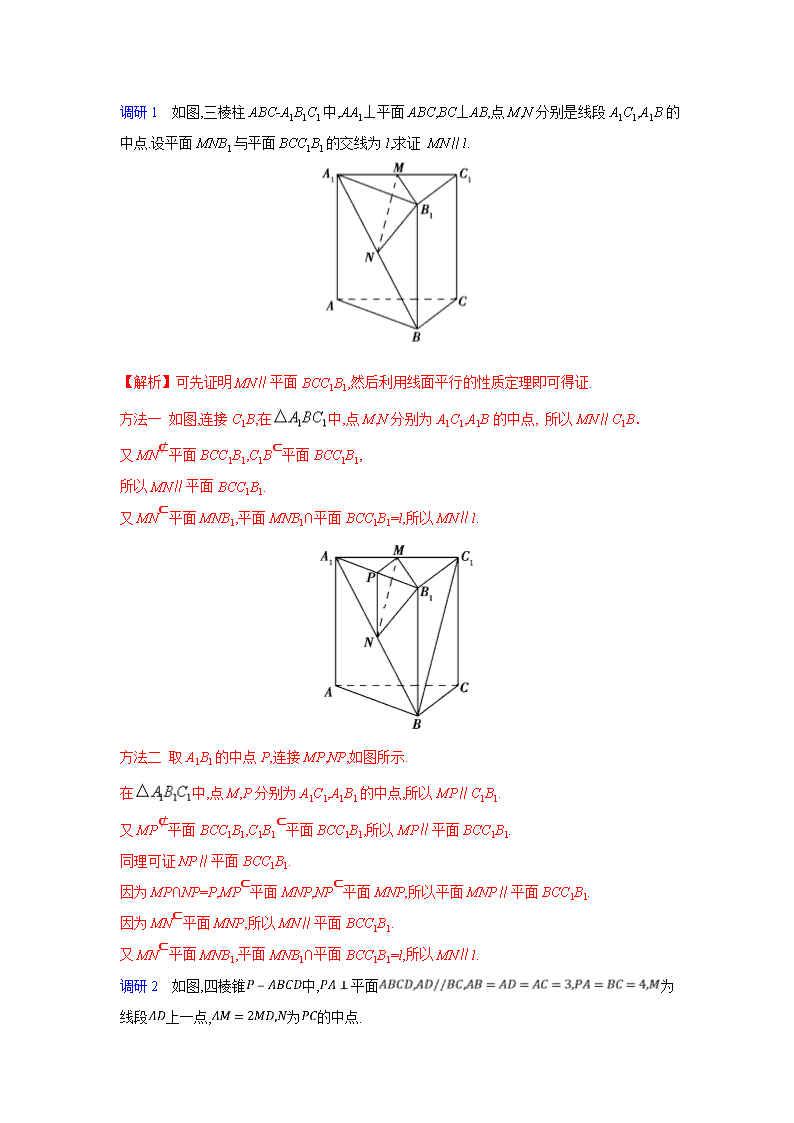调研1 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AB,点M,N分别是线段A1C1,A1B的中点.设平面MNB1与平面BCC1B1的交线为l,求证 MN∥l.‎ ‎【解析】可先证明MN∥平面BCC1B1,然后利用线面平行的性质定理即可得证.‎ 方法一 如图,连接C1B,在中,点M,N分别为A1C1,A1B的中点, 所以MN∥C1B．‎ 又MN⊄平面BCC1B1,C1B⊂平面BCC1B1,‎ 所以MN∥平面BCC1B1. ‎ 又MN⊂平面MNB1,平面MNB1∩平面BCC1B1=l,所以MN∥l.‎ 方法二 取A1B1的中点P,连接MP,NP,如图所示.‎ 在中,点M,P分别为A1C1,A1B1的中点,所以MP∥C1B1.‎ 又MP⊄平面BCC1B1,C1B1⊂平面BCC1B1,所以MP∥平面BCC1B1.‎ 同理可证NP∥平面BCC1B1.‎ 因为MP∩NP=P,MP⊂平面MNP,NP⊂平面MNP,所以平面MNP∥平面BCC1B1.‎ 因为MN⊂平面MNP,所以MN∥平面BCC1B1.‎ 又MN⊂平面MNB1,平面MNB1∩平面BCC1B1=l,所以MN∥l.‎ 调研2 如图,四棱锥中,平面为线段上一点,为的中点.‎ ‎(1)证明 ‎ ‎(2)求四面体的体积.‎ ‎【解析】(1)由已知得,取的中点,连接,由为中点知,即 又,即故四边形为平行四边形,于是 因为所以.‎ ‎(2)因为平面为的中点,所以到平面的距离为 取的中点,连接, ‎ 由得 由得到的距离为,‎ 故,‎ 所以四面体的体积为 题组二 垂直的判定及性质 调研3 如图,在四棱锥中,底面为正方形,平面底面,，点，分别是，的中点.‎ ‎（1）求证 平面；‎ ‎（2）求证 平面；‎ ‎（3）在棱上求作一点，使得，并说明理由.‎ ‎【解析】（1）因为点，分别是，的中点，所以 因为四边形BCDE为正方形，所以 所以 因为平面，平面，所以平面 ‎ ‎（2）因为平面底面，，所以平面 因为平面，所以 因为，点是的中点，所以 因为，平面，平面，‎ 所以平面 ‎ ‎（3）取中点，连接，，过点作，交于点. 则点即为所求作的点.‎ 理由 因为，点是的中点，所以 因为平面底面，所以平面，‎ 所以 ‎ 因为，，所以平面 因为平面，所以 ‎☆技巧点拨☆‎ 空间平行与垂直关系的证明主要是转化思想的应用，如下图 ‎ 在解决平行(垂直)关系的判定时，一般遵循从“低维”到“高维”的转化；而应用性质定理时，其顺序则正好相反．在实际应用中，判定定理和性质定理一般要相互结合，灵活运用．‎ 题组三 线面角与二面角 调研4 如图所示,在四棱锥中,平面平面.‎ ‎ ‎ ‎(1)求证 ;‎ ‎(2)若二面角为,求直线与平面所成的角的正弦值.‎ ‎【解析】(1)在中,应用余弦定理得,解得.‎ 所以,所以. ‎ 因为平面平面,平面平面,所以平面.‎ 又因为平面,所以.‎ ‎(2)因为平面平面,所以.‎ 又,平面平面,‎ 所以是平面与平面所成的二面角的平面角,即.‎ 因为,所以平面.‎ 所以是直线与平面所成的角.‎ 因为在中,,‎ 所以在中,.即直线与平面所成的角的正弦值为.‎ 调研5 已知三棱柱在底面ABC上的射影恰为的中点，.‎ ‎(1)求证 平面;‎ ‎(2)求二面角的余弦值.‎ ‎【解析】(1)由题意知平面,且,‎ 又平面平面平面.‎ 又平面,‎ 又平面,‎ 又，且为平面内的两条相交直线，‎ 平面. ‎ ‎(2)设与的交点为,则由(1)有平面.‎ 过点作于,连,则.‎ 故为所求二面角的平面角.‎ 平面,.‎ 由为中点,得，则.‎ 又在中,得.‎ 在中,，得,‎ 即二面角的余弦值为. ‎ ‎☆技巧点拨☆‎ 记住以下几个常用结论 ‎ ‎(1)夹在两个平行平面之间的平行线段长度相等．‎ ‎(2)经过平面外一点有且只有一个平面与已知平面平行．‎ ‎(3)两条直线被三个平行平面所截，截得的对应线段成比例．‎ ‎(4)如果两个平面分别平行于第三个平面，那么这两个平面互相平行．‎ ‎(5)垂直于同一条直线的两个平面平行．‎ ‎(6)过一点有且只有一条直线与已知平面垂直．‎ ‎(7)过一点有且只有一个平面与已知直线垂直．‎ 考点3 平面图形的翻折与存在性问题 题组一 翻折问题 调研1 如图,已知矩形中,,将矩形沿对角线把折起,使移动到点,且在平面上的射影恰好在上.‎ ‎(1)求证 ;‎ ‎(2)求证 平面平面;‎ ‎(3)求三棱锥的体积.‎ ‎【解析】(1)因为在平面上的射影恰好在上，所以平面,‎ 又平面,所以,‎ 又，所以平面,‎ 又平面,所以.‎ ‎(2)因为是矩形,所以,‎ 由(1)知,‎ 所以平面,‎ 又平面,所以平面平面.‎ ‎(3)因为平面,所以,‎ 因为==,所以, ‎ 所以===.‎ ‎☆技巧点拨☆‎ 折叠与展开，这两种方式的转变是空间几何与平面几何问题转化的集中体现，求解翻折问题的关键是把握翻折前后的变量和不变量．‎ 题组二 探索性问题 调研2 如图,平行四边形中,==,现将沿折起,得到三棱锥,且,点为侧棱的中点.‎ ‎(1)求证 平面;‎ ‎(2)求三棱锥的体积;‎ ‎(3)在的角平分线上是否存在一点,使得平面?若存在,求的长;若不存在,请说明理由.‎ ‎【解析】(1)在平行四边形中,有,‎ 又因为为侧棱的中点,所以,‎ 又因为,且,所以平面,‎ 又因为平面,所以,‎ 因为,所以平面.‎ ‎(2)因为平面,所以是三棱锥的高,‎ 故==. ‎ ‎(3)取中点,连接并延长至点,使,连接,OE，‎ 因为,所以射线是角的角平分线,‎ 又因为点是中点,所以,‎ 因为平面平面,所以平面,‎ 因为互相平分,所以四边形为平行四边形,则,‎ 又因为,所以===. ‎ ‎☆技巧点拨☆‎ ‎(1)推理型探索性问题 推理型探索性问题，以探究空间中直线、平面的平行与垂直关系为主，解决此类问题主要采用直接法，即利用空间平行与垂直关系的判定与性质定理进行逻辑推理，将其转化为平面图形中的线线关系进行探究，逻辑推理的思维量较大．‎ ‎(2)计算型探索性问题 计算型探索性问题，主要是对几何体的表面积、体积或距离等问题进行有关探究．解决此类问题主要采用直接法，即利用几何体的结构特征，巧设未知量，将所探究的问题转化为建立关于所设未知量的函数或方程，依据目标函数的性质或方程解的存在性求解．‎ ‎ ‎ ‎1．（2017-2018 年贵州省遵义市航天高级中 高三上 期模拟考试）设表示三条直线, 表示三个平面,则下列命题中不成立的是 A．若∥,则∥‎ B．若∥,则 C．若是在内的射影,,则 D．若,则 ‎【答案】D ‎ 2．（2017-2018 年南宁市高三毕业班摸底联考）在如图所示的正方体中分别是棱的中点,则异面直线与所成角的余弦值为 A． B．‎ C． D．‎ ‎【答案】D ‎【解析】取DD1的中点G,连接BG,FG,易知四边形BED1G是平行四边形,则BG//ED1,则∠FBG（或其补角）等于异面直线与所成的角,令正方体的棱长为2,则BF=FG=BG=3，从而cos∠FBG=.则异面直线与所成角的余弦值为.‎ ‎3．（云南省昆明市第一中 2018届高三第五次月考）已知表示两个不同的平面，表示一条直线，且，则是的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【答案】D ‎【解析】由题意，，，则或，所以充分条件不成立；又当，‎ 时，不能得到，所以必要条件不成立，故选D． ‎ ‎4．（2018届四川省泸县第二中 高三上 期期末考试）在直三棱柱ABC-A1B1C1中,AB＝1,AC＝2,BC＝,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为 A．30° B．45°‎ C．60° D．90°‎ ‎【答案】A ‎5．（陕西省渭南市2018届高三教 质量检测（I））二面角的棱上有，两点，直线，分别在这个二面角的两个半平面内，且都垂直于，已知， ， ， ，则该二面角的大小为 A． B．‎ C． D．‎ ‎【答案】B ‎6．（福建省闽侯第四中 2018届高三上 期期末考试）如图是一几何体的平面展开图，其中为正方形，，分别为，的中点，在此几何体中，给出下面四个结论 ‎ ‎①直线与直线异面； ②直线与直线异面；‎ ‎③直线平面； ④平面平面.‎ 其中正确的有 A．个 B．个 C．个 D．个 ‎【答案】B ‎ ‎【解析】将几何体展开图还原为几何体，如图所示 ‎ ‎①项，分别为的中点，，即直线与共面，故错误；‎ ‎②项，平面，平面，，与是异面直线，故正确；‎ ‎③项，，平面，平面，平面，故正确；‎ ‎④项，平面与平面不一定垂直，故错误.‎ 综上所述，正确的有2个.故选B.‎ ‎7．（山东省济南市长清第一中 大 技园校区2017- 2018 年高三质量检测）‎ 如图所示，在正方体中，，分别是棱和上的点，若是直角，则等于_______．‎ ‎【答案】‎ ‎8．（北京市海淀区2018届高三第一 期期末）已知正方体的棱长为，点是棱的中点，点在底面内，点在线段上，若，则的最小值为__________.‎ ‎【答案】‎ ‎9．（2017-2018 年河北省定州中 高三上 期期中考试）如图,在正方形ABCD中,E、F分别是的中点,G是EF的中点.现在沿及EF把这个正方形折成一个空间图形,使三点重合,重合后的点记为下列说法错误的是__________ (将符合题意的选项序号填到横线上).‎ ‎①所在平面; ②所在平面; ‎ ‎③所在平面; ④所在平面.‎ ‎【答案】①③④‎ ‎【解析】①根据条件,所以,故AG不可能垂直于平面,所以错误;②正确;③若,则,显然一个三角形中不能有两个直角,错误;④若,则中有两个直角,错误,故填①③④. ‎ ‎10．（河北衡水金卷2018届高三高考模拟）如图，在直角梯形中，，， ，点是线段上异于点，的动点， 于点，将沿折起到的位置，并使，则五棱锥的体积的取值范围为__________．‎ ‎【答案】‎ ‎11．（江苏省淮安市等四市2018届高三上 期第一次模拟）如图，在直三棱柱中， ，，，分别是，的中点.‎ ‎ 求证 （1）平面；‎ ‎（2）.‎ ‎【解析】（1）如图，取的中点，连接 ‎ 因为分别是的中点，所以且 在直三棱柱中，，，‎ 又因为是的中点，所以且，所以四边形是平行四边形，‎ 所以，‎ 而平面，平面，所以平面. ‎ ‎ ‎ ‎12．（2017-2018 年西藏拉萨市高三第一次模拟考试）如图,四棱锥的底面为等腰梯形,且,点为中点．‎ ‎(1)证明 平面;‎ ‎(2)若平面,直线与平面所成角的正切值为，求四棱锥的体积．‎ ‎ ‎ ‎(2)作于点,则．‎ 在中,,则．‎ 由平面知,直线与平面所成的角为,故,‎ 即在中,有,则.‎ 所以,四棱锥的体积．‎ ‎13．（河北省衡水中 2018届高三上 期九模）如图，在长方体中， 分别为的中点，是上一个动点，且.‎ ‎（1）当时，求证 平面平面；‎ ‎（2）是否存在，使得？若存在，请求出的值；若不存在，请说明理由.‎ 则，即.‎ ‎14．（2018届天津市耀华中 高三上 期第一次月考）如图,在直三棱柱中,‎ 是的中点,是的中点.‎ ‎ ‎ ‎(1)求异面直线与所成的角;‎ ‎(2)求证 ;‎ ‎(3)求二面角的正切值.‎ ‎15．（2017-2018 年江西省南昌市第二中 高三上 期第四次考试）如图,在矩形中,分别为的中点,现将沿折起,得四棱锥.‎ ‎(1)求证 EF//平面;‎ ‎(2)若平面平面,求四面体的体积.‎ ‎【解析】(1)取线段的中点,连接,‎ 因为为的中点,所以,且,‎ ‎16．（贵州省贵阳市第一中 2018届高三12月月考）如图，为圆柱的母线，是底面圆的直径，是的中点.‎ ‎（1）问 上是否存在点，使得平面？请说明理由；‎ ‎（2）在（1）的条件下，若平面，假设这个圆柱是一个大容器，有条体积可以忽略不计的小鱼能在容器的任意地方游弋，如果小鱼游到四棱锥 外会有被捕的危险，求小鱼被捕的概率.‎ ‎ ‎ ‎ ‎ ‎1．（2016新课标全国Ⅱ理 ）α，β是两个平面，m，n是两条直线，有下列四个命题 ‎ ‎①如果m⊥n，m⊥α，n∥β，那么α⊥β.‎ ‎②如果m⊥α，n∥α，那么m⊥n.‎ ‎③如果α∥β，mα，那么m∥β.‎ ‎④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等.‎ 其中正确的命题有 .(填写所有正确命题的编号）‎ ‎【答案】②③④‎ ‎【名师点睛】求解本题时应注意在空间中考虑线面位置关系.‎ ‎2．（2017新课标全国Ⅰ理 节选）如图，在四棱锥P−ABCD中，AB//CD，且.‎ 证明 平面PAB⊥平面PAD．‎ ‎【解析】由已知，得AB⊥AP，CD⊥PD．‎ 由于AB//CD ，故AB⊥PD ，从而AB⊥平面PAD．‎ 又AB 平面PAB，‎ 所以平面PAB⊥平面PAD．‎ ‎3．（2016新课标全国Ⅲ理 节选）如图，四棱锥P−ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.证明MN∥平面PAB．‎ ‎【解析】由已知得.‎ 取的中点，连接，由为中点知，．‎ 又，故，四边形为平行四边形，于是.‎ 因为平面， 平面，‎ 所以平面．‎ ‎4． (2015新课标全国I理 节选)如图,四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC．‎ 证明 平面AEC⊥平面AFC；‎ 在直角梯形BDFE中，由BD=2，BE=，DF=可得EF=，‎ ‎∴，∴EG⊥FG，‎ ‎∵AC∩FG=G，∴EG⊥平面AFC，‎ ‎∵EG面AEC，∴平面AFC⊥平面AEC． ‎ ‎5．（2016新课标全国Ⅱ理 节选）如图，菱形ABCD的对角线AC与BD交于点O，AB=5，AC=6，点E，F分别在AD，CD上，AE=CF=，EF交BD于点H. 将△DEF沿EF折到△的位置，.‎ 证明 平面ABCD．‎