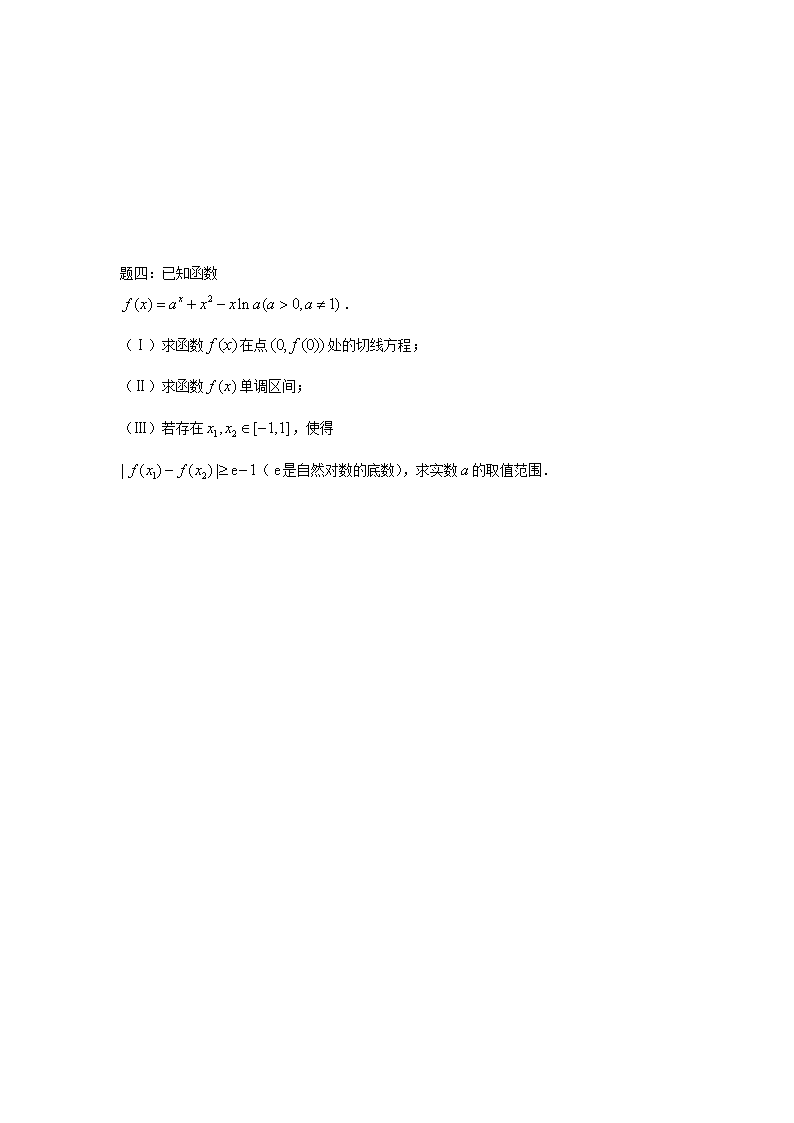【数学】2019届一轮复习苏教版第3讲函数、导数与方程、不等式综合问题经典精讲学案 5页

第3讲 函数、导数与方程、不等式综合问题经典精讲 题一：设函数，‎ 证明：（Ⅰ）当时，；‎ ‎（Ⅱ）.‎ 题二：已知函数，，求证：.‎ 题三：已知函数.‎ 证明：（Ⅰ）当时，；‎ ‎（Ⅱ）当时，. ‎ 题四：已知函数 ‎．‎ ‎（Ⅰ）求函数在点处的切线方程；‎ ‎（Ⅱ）求函数单调区间；‎ ‎（Ⅲ）若存在，使得 ‎（是自然对数的底数），求实数的取值范围．‎ 函数、导数与方程、不等式综合问题经典精讲 题一：证明（Ⅰ）：因为 所以在定义域内单调递增， ‎ 当时，，故（Ⅰ）成立；‎ ‎（Ⅱ）由（Ⅰ）得当时，，‎ 所以，‎ 即，‎ 亦即，‎ 所以，此题得证.‎ 题二：证明：法一：因为，‎ 所以原不等式等价于 ‎，‎ 令，‎ ‎，‎ 则，‎ 所以在上单调递减，‎ 所以，此题得证；‎ 法二：设，‎ 因为，‎ 所以在上单调递增，即，‎ 所以，‎ ‎，‎ 所以，此题得证.‎ 题三：因为 所以单调递增，‎ ‎（Ⅰ）当时，‎ ‎，此题得证；‎ ‎（Ⅱ）法一：令 ‎，‎ 则，，‎ 由（Ⅰ）得，‎ 所以，‎ 所以在上单调递减，‎ 所以，‎ 所以在上单调递减，‎ 所以，‎ 即，此题得证；‎ 法二：令，‎ 则 ‎，‎ 由（Ⅰ）得，所以 所以在上单调递减，所以，‎ 即，此题得证.‎ 题四：（Ⅰ）‎ ‎（Ⅱ）在上单调递减，在上单调递增 ‎（Ⅲ）‎