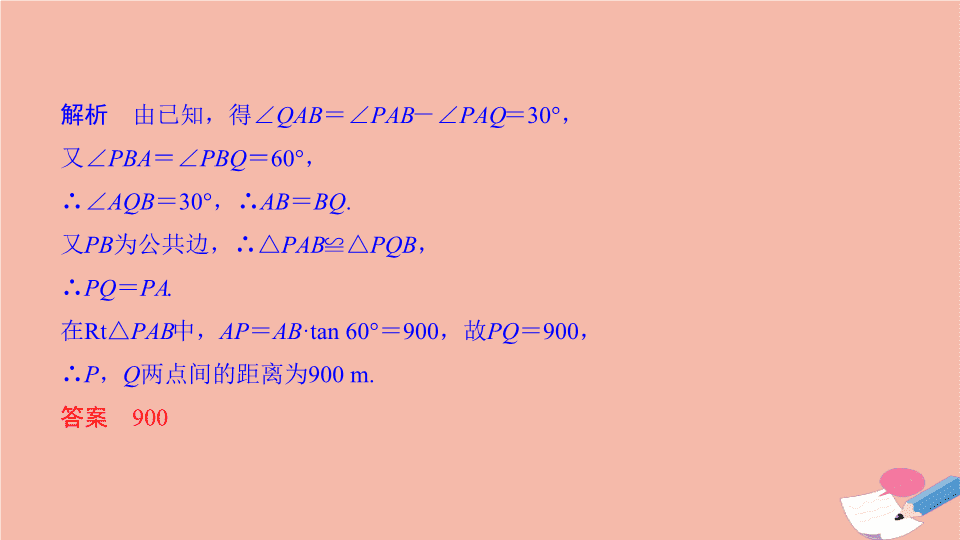2021届高考数学一轮复习第四章三角函数解三角形第6节第二课时解三角形的综合应用课件新人教A版 27页

第二课时　解三角形的综合应用 考点一　解三角形的实际应用　 多维探究 角度 1 　测量距离问题 解析　 由已知，得 ∠ QAB ＝ ∠ PAB － ∠ PAQ ＝ 30° ， 又 ∠ PBA ＝ ∠ PBQ ＝ 60° ， ∴∠ AQB ＝ 30° ， ∴ AB ＝ BQ . 又 PB 为公共边， ∴△ PAB ≌△ PQB ， ∴ PQ ＝ PA . 在 Rt △ PAB 中， AP ＝ AB ·tan 60° ＝ 900 ，故 PQ ＝ 900 ， ∴ P ， Q 两点间的距离为 900 m. 答案　 900 规律方法　 距离问题的类型及解法： (1) 类型：两点间既不可达也不可视，两点间可视但不可达，两点都不可达 . (2) 解法：选择合适的辅助测量点，构造三角形，将问题转化为求某个三角形的边长问题，从而利用正、余弦定理求解 . 角度 2 　测量高度问题 【例 1 － 2 】 如图，测量河对岸的塔高 AB 时可以选与塔底 B 在同一水平面内的两个测点 C 与 D ，测得 ∠ BCD ＝ 15° ， ∠ BDC ＝ 30° ， CD ＝ 30 ，并在点 C 测得塔顶 A 的仰角为 60° ，则塔高 AB 等于 ( 　　 ) 解析　 在 △ BCD 中， ∠ CBD ＝ 180° － 15° － 30° ＝ 135°. 规律方法　 1. 在测量高度时，要理解仰角、俯角的概念，仰角和俯角都是在同一铅垂面内，视线与水平线的夹角 . 2. 准确理解题意，分清已知条件与所求，画出示意图 . 3. 运用正、余弦定理，有序地解相关的三角形，逐步求解问题的答案，注意方程思想的运用 . 角度 3 　测量角度问题 【例 1 － 3 】 已知岛 A 南偏西 38° 方向，距岛 A 3 海里的 B 处有一艘缉私艇 . 岛 A 处的一艘走私船正以 10 海里 / 时的速度向岛屿北偏西 22° 方向行驶，问缉私艇朝何方向以多大速度行驶，恰好用 0.5 小时能截住该走私船？ 解　 如图，设缉私艇在 C 处截住走私船， D 为岛 A 正南方向上一点，缉私艇的速度为每小时 x 海里，则 BC ＝ 0.5 x ， AC ＝ 5 ，依题意， ∠ BAC ＝ 180° － 38° － 22° ＝ 120° ， 由余弦定理可得 BC 2 ＝ AB 2 ＋ AC 2 － 2 AB · AC cos 120° ， 所以 BC 2 ＝ 49 ，所以 BC ＝ 0.5 x ＝ 7 ，解得 x ＝ 14. 又 ∠ BAD ＝ 38° ，所以 BC ∥ AD ， 故缉私艇以每小时 14 海里的速度向正北方向行驶，恰好用 0.5 小时截住该走私船 . 规律方法　 1. 测量角度问题的关键是在弄清题意的基础上，画出表示实际问题的图形，并在图形中标出有关的角和距离，再用正弦定理或余弦定理解三角形，最后将解得的结果转化为实际问题的解 . 2. 方向角是相对于某点而言的，因此在确定方向角时，必须先弄清楚是哪一个点的方向角 . 【训练 1 】 (1) ( 角度 1) 江岸边有一炮台高 30 m ，江中有两条船，船与炮台底部在同一水平面上，由炮台顶部测得俯角分别为 45° 和 60° ，而且两条船与炮台底部连线成 30° 角，则两条船相距 ________m. (2) ( 角度 2) 如图，一辆汽车在一条水平的公路上向正西行驶，到 A 处时测得公路北侧一山顶 D 在西偏北 30° 的方向上，行驶 600 m 后到达 B 处，测得此山顶在西偏北 75° 的方向上，仰角为 30° ，则此山的高度 CD ＝ ________m. (3) ( 角度 3) 如图，两座相距 60 m 的建筑物 AB ， CD 的高度分别为 20 m ， 50 m ， BD 为水平面，则从建筑物 AB 的顶端 A 看建筑物 CD 的张角 ∠ CAD 等于 ( 　　 ) A.30° B.45° C.60° D.75° 解析　 (1) 如图，设炮台的顶部为 A ，底部为 O ，两只小船分别为 M ， N ，则由题意得， OM ＝ AO tan 45° ＝ 30(m) ， 在 △ MON 中，由余弦定理得， (2) 由题意，在 △ ABC 中， ∠ BAC ＝ 30° ， ∠ ABC ＝ 180° － 75° ＝ 105° ，故 ∠ ACB ＝ 45°. 所以在 △ ACD 中，由余弦定理得 又 0°< ∠ CAD <180° ，所以 ∠ CAD ＝ 45° ， 所以从顶端 A 看建筑物 CD 的张角为 45°. 考点二　解三角形与三角函数的综合应用 规律方法　 解三角形与三角函数的综合应用主要体现在以下两方面： (1) 利用三角恒等变换化简三角函数式进行解三角形； (2) 解三角形与三角函数图象和性质的综合应用 . 考点三　正、余弦定理在平面几何中的应用 【例 3 】 (2020· 河南、河北重点中学联考 ) 如图，在 △ ABC 中，内角 A ， B ， C 的对边分别为 a ， b ， c ，已知 c ＝ 4 ， b ＝ 2 ， 2 c cos C ＝ b ， D ， E 分别为线段 BC 上的点，且 BD ＝ CD ， ∠ BAE ＝ ∠ CAE . (1) 求线段 AD 的长； (2) 求 △ ADE 的面积 . 所以 a ＝ 4 ，即 BC ＝ 4. 在 △ ACD 中， CD ＝ 2 ， AC ＝ 2 ， 所以 AD 2 ＝ AC 2 ＋ CD 2 － 2 AC · CD ·cos ∠ ACD ＝ 6 ， (2) 因为 AE 是 ∠ BAC 的平分线， 规律方法　 平面几何中解三角形问题的求解思路 (1) 把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解 . (2) 寻找各个三角形之间的联系，交叉使用公共条件，求出结果 . 提醒　 做题过程中，要用到平面几何中的一些知识点，如相似三角形的边角关系、平行四边形的一些性质，要把这些性质与正弦、余弦定理有机结合，才能顺利解决问题 . 又 A ＋ B ＋ C ＝ π ，所以 sin B ＝ sin( A ＋ C ) ， 解得 t ＝ 1 ，即 a ＝ 8 ， b ＝ 5 ， c ＝ 7. 因为 BD ＝ 3 DC ，所以 BD ＝ 6 ， DC ＝ 2. 在 △ ADC 中，由余弦定理，得 AD 2 ＝ CD 2 ＋ CA 2 － 2 CD · CA ·cos C ＝ 19 ，