云南省曲靖市会泽县茚旺高级中学2019-2020学年高一下学期开学考试数学考试题 15页

数学 考生注意：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共22个小题，总分150分，考试时间120分钟，在答题卡上答题，做在试卷上无效.‎ 第Ⅰ卷（选择题，共60分）‎ 一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个选项符合要求)‎ ‎1.已知集合，，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 解不等式简化集合的表示，用列举法表示集合，最后根据集合交集的定义求出.‎ ‎【详解】，，‎ 又，所以，故本题选C.‎ ‎【点睛】本题考查了列举法表示集合、集合交集的运算，正确求解出不等式的解集是解题的关键.‎ ‎2.函数(　　)‎ A. 是奇函数 B. 是偶函数 C. 是非奇非偶函数 D. 既是奇函数又是偶函数 ‎【答案】C ‎【解析】‎ 函数的定义域为[0，＋∞)，不关于原点对称，所以函数f(x)是非奇非偶函数．‎ 答案：C.‎ ‎3.设函数f(x)＝则f(f(3))＝(　　)‎ A. B. ‎3 ‎C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【详解】,‎ ‎,故选D.‎ ‎4.半径为的半圆卷成一个圆锥，则它的体积是（ ）‎ A. B. C. D. 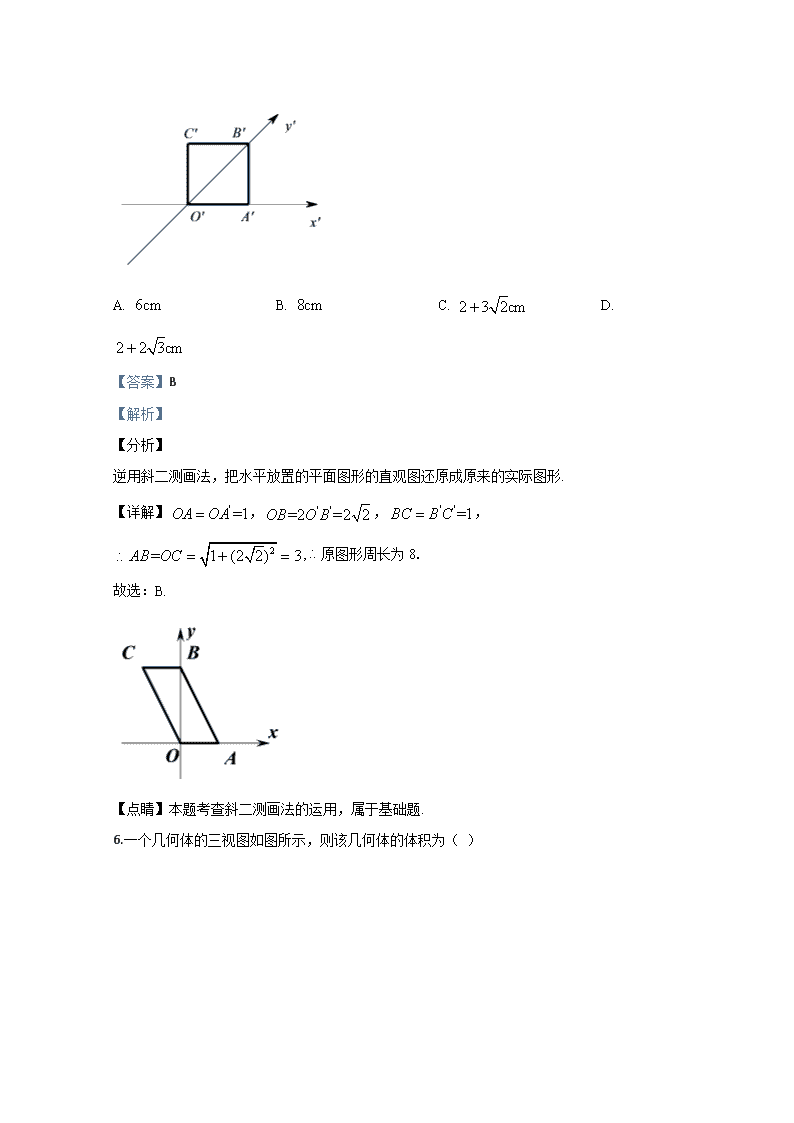‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 求出扇形的弧长，然后求出圆锥的底面周长，转化为底面半径，求出圆锥的高，然后求出体积．‎ ‎【详解】设底面半径为r，则，所以.‎ 所以圆锥的高.‎ 所以体积.‎ 故选：C.‎ ‎【点睛】本题考查圆锥的性质及体积，圆锥问题抓住两个关键点：（1）圆锥侧面展开图的扇形弧长等于底面周长；（2）圆锥底面半径r、高h、母线l组成直角三角形，满足勾股定理，本题考查这两种关系的应用，属于简单题.‎ ‎5.如图所示，正方形的边长为，它是水平放置的一个平面图形的直观图，则原图形的周长是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 逆用斜二测画法，把水平放置的平面图形的直观图还原成原来的实际图形.‎ ‎【详解】，，，‎ ‎,原图形周长为8.‎ 故选：B.‎ ‎【点睛】本题考查斜二测画法的运用，属于基础题.‎ ‎6.一个几何体的三视图如图所示，则该几何体的体积为（ ）‎ A. 2 B. ‎1 ‎C. D. ‎ ‎【答案】C ‎【解析】‎ 试题分析：由已知中的三视图，我们可以判断出该几何体的几何特征，该几何体是一个四棱锥其底面是一个对角线为2的正方形，面积S=,高为1,则体积V=，故选C.‎ 考点：本题考查的知识点是由三视图求体积.‎ 点评：根据已知中的三视图判断该物体是一个底面为对角为2的正方形，高为1的四棱锥是解答本题的关键.‎ ‎7.在同一直角坐标系中，函数的图像可能是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 通过分析幂函数和对数函数的特征可得解.‎ ‎【详解】函数，与，‎ 答案A没有幂函数图像，‎ 答案B.中，中，不符合，‎ 答案C中，中，不符合，‎ 答案D中，中，符合，故选D.‎ ‎【点睛】本题主要考查了幂函数和对数函数的图像特征，属于基础题.‎ ‎8.函数的一个零点在区间内，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由题意得，解不等式可得实数a的取值范围．‎ ‎【详解】由条件可知，即a(a－3)<0，‎ 解得0