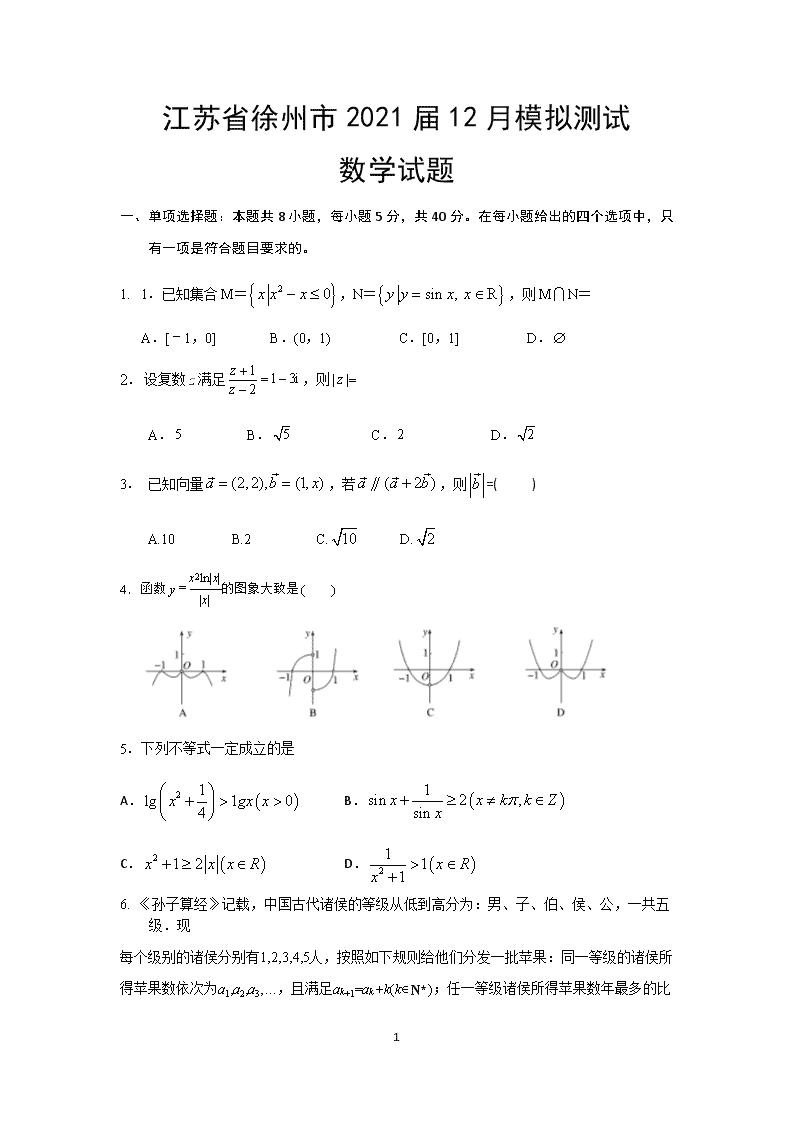江苏省徐州市2021届高三上学期12月模拟测试数学试题 6页

1 江苏省徐州市 2021 届 12 月模拟测试 数学试题 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的四个选项中，只 有一项是符合题目要求的。 1. 1．已知集合 M＝ 2 0x x x  ，N＝ sin , Ry y x x  ，则 M  N＝ A．[﹣1，0] B．(0，1) C．[0，1] D．  2．设复数 满足 1 1 3i2 z z    ，则| |z  A．5 B． 5 C． 2 D． 2 3． 已知向量 (2,2), (1, )a b x  ，若 ( 2 )a a b   ，则 b  =( ) A.10 B.2 C. 10 D. 2 4．函数 y＝x2ln|x| |x| 的图象大致是( ) 5．下列不等式一定成立的是 A．  2 1lg 1 04x gx x      B．  1sin 2 ,sinx x k k Zx     C．  2 1 2x x x R   D．  2 1 1 x Rx   6. 《孙子算经》记载，中国古代诸侯的等级从低到高分为：男、子、伯、侯、公，一共五级．现 每个级别的诸侯分别有1,2,3,4,5人，按照如下规则给他们分发一批苹果：同一等级的诸侯所 得苹果数依次为a1,a2,a3,…，且满足ak+1=ak +k(kN*)；任一等级诸侯所得苹果数年最多的比 高一级的诸侯所得苹果数最少的少一个．现已知等级为男的诸侯所得苹果数为1,则这批苹果 共有( )个． A. 158 B. 159 C. 160 D.161 7 ． 设 函 数  f x 为 奇 函 数 ， 且 当 0x  时 ，   cosxf x e x  ， 则 不 等 式    2 1 2 0f x f x    的解集为( ) A.  ,1 B. 1, 3     C. 1,3     D.  1, 2 8．函数 ( ) 4ln 3f x x ax   存在两个不同的零点 1 2,x x ，函数 2( ) 2g x x ax   存在两 个不同的零 点 3 4,x x ，且满足 3 1 2 4x x x x   ，则实数 a 的取值范围是（ ） A． 0,3 B． 2 2,3 C． 1 42 2,4e       D． 1 43,4e       二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分。在每小题给出的选项中，有多项 符合题目要求。全部选对的得 5 分，部分选对的得 3 分，有选错的得 0 分。 9．已知 2( ) 2sin cos 2 3cos 3f x x x x   ，下列说法正确的有 A． ( )f x 的最小正周期是 2 B． ( )f x 最大值为 2 C． ( )f x 的图象关于 3x  对称 D． ( )f x 的图象关于 2 ,03     对称 10． “双11”购物节中，某电商对顾客实行购物优惠活动，规定一次购物付款总额满一定额 度，可以给与优惠： （1）如果购物总额不超过 50元，则不给予优惠； （2）如果购物总额超过50元但不超过100元，可以使用一张 5元优惠劵； （3）如果购物总额超过100元但不超过300元，则按标价给予 9折优惠； （4）如果购物总额超过300元，其中300元内的按第（3）条给予优惠，超过300元的部 分给予8 折优惠． 某人购买了部分商品，则下列说法正确的是（ ） A．如果购物总额为 78元，则应付款为 73元 B．如果购物总额为 228 元，则应付款为 205.2 元 C．如果购物总额为368元，则应付款为 294.4 元 D．如果购物时一次性全部付款 442.8 元，则购物总额为516元 11．已知数列 na 是等比数列，则下列结论中正确的是 A．数列 2 na 是等比数列 B．若 3 72, 32a a  ，则 5 8a   C．若数列 na 的前 n 项和 13 1n nS r r   ，则 D．若 1 2 3a a a  ，则数列 na 是递增数列 3 12．椭圆 2 2 2 2: 1( 0)x yC a ba b     ， 1F ， 2F 分别为左、右焦点， 1A ， 2A 分别为左、右顶 点，P 为椭圆上的动点，且 1 2 1 2 0PF PF PA PA       恒成立，则椭圆 C 的离心率可能为 （ ） A． 1 2 B． 2 2 C． 3 3 D． 3 2 三、填空题：本题共 4 小题，每小题 5 分，共 20 分。请把答案直接填写在答题卡相应．．．．． 位置上．．．。 13．已知函数 2log , 0, ( ) 2 2, 0,x x x f x x    ≤ ，则 1( ( ))2f f = ． 14．已知正实数 a ，b 满足 2 ( 2 ) 4ab a b  ，则 a b 的最小值为 ． 15．一元线性同余方程组问题最早可见于中国南北朝时期(公元 5 世纪)的数学著作《孙子算 经》卷下第二十六题，叫做“物不知数”问题，原文如下：有物不知数，三三数之剩二， 五五数之剩三，问物几何?即，一个整数除以三余二，除以五余三，求这个整数．设这个 整数为  2,2019a a，当 时，符合条件的 a 共有________个． 16．在棱长为 2 的正方体 1 1 1 1ABCD A B C D ，中，E，F 分别为棱 1 1A B ， 1 1B C 的中点，点 P 在线段 EF 上，则三棱锥 1P D AC 的体积为________． 四、解答题：本题共 6 小题，共 70 分。请在答题卡指定区域．．．．．．．内作答。解答时应写出文字说 明、证明过程或演算步骤。 17．(本小题满分 10 分 ) 已知角 的终边与单位圆 122  yx 在第四象限交于点 P ，且点 P 的坐标为 1( , )2 y ． （1）求 tan 的值； （2）求 cos( ) cos( 2 )2 sin cos( )             的值． 4 18．(本小题满分 12 分) 已知等比数列{ }na 满足 1a ， 2a ， 3 1a a 成等差数列，且 1 3 4a a a ；等差数列{ }nb 的前 n 项和 2( 1)log 2 n n n aS  ．求： （1） na ， nb ； （2）数列{ }n na b 的前项和 nT ． 19．(本小题满分 12 分) 如图，在四棱锥 P－ABCD 中，底面 ABCD 是正方形，AC 与 BD 交于点 O， PC⊥底面 ABCD， 点 E 为侧棱 PB 的中点． 求证：(1) PD∥平面 ACE； (2) 平面 PAC⊥平面 PBD． 20．(本小题满分 12 分) 2017 年 11 月河南省三门峡市成功入围“十佳魅力中国城市”，吸引了大批投资商的目光， 一些投资商积极准备投入到“魅力城市”的建设之中．某投资公司准备在 2018 年年初将四百 万元投资到三门峡下列两个项目中的一个之中． 项目一：天坑院是黄土高原地域独具特色的民居形式，是人类“穴居”发展史演变的实物见 证．现准备投资建设 20 个天坑院，每个天坑院投资 0.2 百万元，假设每个天坑院是否盈利 是相互独立的，据市场调研，到 2020 年底每个天坑院盈利的概率为 (0 1)p p  ，若盈利则 盈利投资额的 40% ，否则盈利额为 0． 项目二：天鹅湖国家湿地公园是一处融生态、文化和人文地理于一体的自然山水景区．据市 场调研，投资到该项目上，到 2020 年底可能盈利投资额的 50% ，也可能亏损投资额的 30% ， 且这两种情况发生的概率分别为 p 和1 p ． （1）记 X （单位：百万元）为投资项目一盈利额，求 ( )E X （用 p 表示）； （2）试以项目盈利的期望为依据，针对以上两个投资项目，请你为投资公司选择一个项目， 并说明理由． 题 19 图 A BC D P O E 5 21．(本小题满分 12 分) 已知椭圆 C： 2 2 2 2 1x y a b   (a＞b＞0)的左右焦点分别为 F1，F2 点．M 为椭圆上的一动点， △MF1F2 面积的最大值为 4．过点 F2 的直线 l 被椭圆截得的线段为 PQ，当 l⊥x 轴时， 2 2PQ  ． (1)求椭圆 C 的方程； (2)过点 F1 作与 x 轴不重合的直线 l，l 与椭圆交于 A，B 两点，点 A 在直线 x=－4 上的投影 N 与点 B 的连线交 x 轴于 D 点，D 点的横坐标 x0 是否为定值?若是，求出定值；若不是，请 说明理由． 22．(本小题满分 12 分) 已知函数 1( )h x x x   ． （1）直接写出 ( )h x 在 1[ ,2]2 上的单调区间（无需证明）； （2）求 ( )h x 在 1 1[ , ] ( )2 2a a  上的最大值； （3）设函数 ( )f x 的定义域为 I ，若存在区间 A I ，满足： 1x A  ， 2 Ix A ð ，使得 1 2( ) ( )f x f x ，则称区间 A 为 ( )f x 的“  区间”．已知 1( )f x x x   （ 1[ ,2]2x ）， 若 1[ , )2A b 是函数 ( )f x 的“  区间”，求实数b 的最大值 ． 6