【数学】2019届一轮复习苏教版集合与常用逻辑用语学案 10页

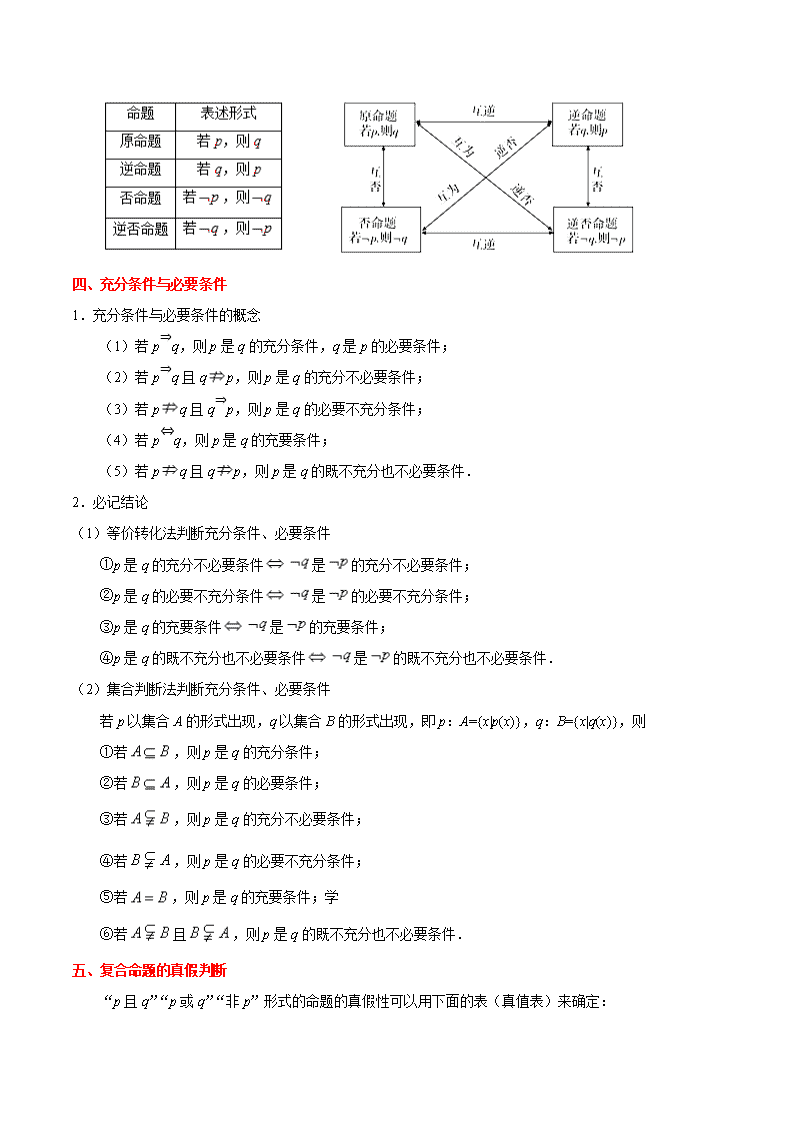
专题01 集合与常用逻辑用语 一、集合间的基本关系 自然语言 符号语言 图示 基 本基本关系 子集 集合A中任意一个元素都是集合B的元素 ‎（或）‎ 真子集 集合A是集合B的子集，且集合B中至少有一个元素不在集合A中 ‎（或）‎ 相等 集合A，B中元素相同或集合A，B互为子集 空集 空集是任何集合的子集，是任何非空集合的真子集 ‎，‎ ‎【必记结论】（1）若集合A中含有n个元素，则有个子集，有个非空子集，有个真子集，有个非空真子集；（2）子集关系的传递性，即．‎ 二、集合的基本运算 运算 自然语言 符号语言 Venn图 交集 由属于集合A且属于集合B的所有元素组成的集合 并集 由所有属于集合A或属于集合B的元素组成的集合 补集 由全集U中不属于集合A的所有元素组成的集合 ‎【必记结论】‎ 三、四种命题及其关系 在数学中用语言、符号或式子表达的，可以判断真假的陈述句叫做命题．其中判断为真的语句叫真命题，判断为假的语句叫假命题．‎ 四种命题及其关系如下：‎ 四、充分条件与必要条件 ‎1．充分条件与必要条件的概念 ‎（1）若p⇒q，则p是q的充分条件，q是p的必要条件；‎ ‎（2）若p⇒q且qp，则p是q的充分不必要条件；‎ ‎（3）若pq且q⇒p，则p是q的必要不充分条件；‎ ‎（4）若p⇔q，则p是q的充要条件；‎ ‎（5）若pq且qp，则p是q的既不充分也不必要条件．‎ ‎2．必记结论 ‎（1）等价转化法判断充分条件、必要条件 ‎①p是q的充分不必要条件是的充分不必要条件；‎ ‎②p是q的必要不充分条件是的必要不充分条件；‎ ‎③p是q的充要条件是的充要条件；‎ ‎④p是q的既不充分也不必要条件是的既不充分也不必要条件．‎ ‎（2）集合判断法判断充分条件、必要条件 若p以集合A的形式出现，q以集合B的形式出现，即p：A={x|p(x)}，q：B={x|q(x)}，则 ‎①若，则p是q的充分条件；‎ ‎②若，则p是q的必要条件；‎ ‎③若，则p是q的充分不必要条件；‎ ‎④若，则p是q的必要不充分条件；‎ ‎⑤若，则p是q的充要条件；学 ‎ ‎⑥若且，则p是q的既不充分也不必要条件．‎ 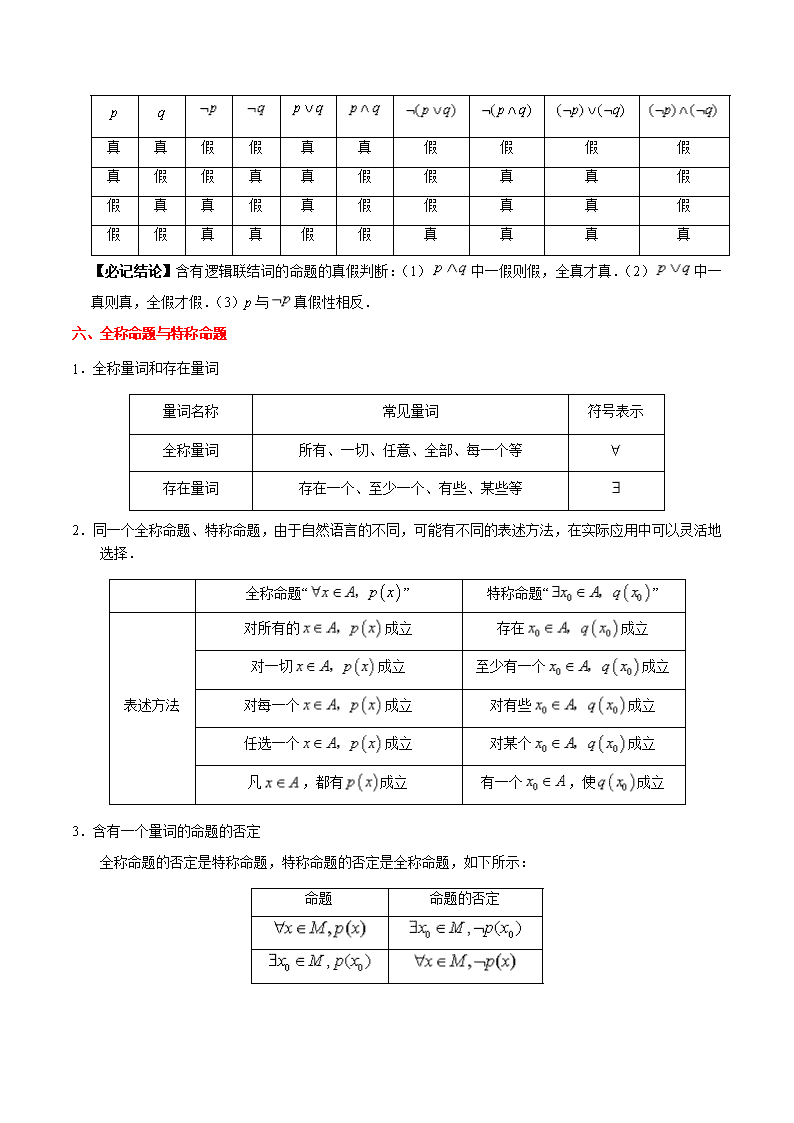五、复合命题的真假判断 ‎“p且q”“p或q”“非p”形式的命题的真假性可以用下面的表（真值表）来确定：‎ p q 真 真 假 假 真 真 假 假 假 假 真 假 假 真 真 假 假 真 真 假 假 真 真 假 真 假 假 真 真 假 假 假 真 真 假 假 真 真 真 真 ‎【必记结论】含有逻辑联结词的命题的真假判断：（1）中一假则假，全真才真．（2）中一真则真，全假才假．（3）p与真假性相反．‎ 六、全称命题与特称命题 ‎1．全称量词和存在量词 量词名称 常见量词 符号表示 全称量词 所有、一切、任意、全部、每一个等 存在量词 存在一个、至少一个、有些、某些等 ‎2．同一个全称命题、特称命题，由于自然语言的不同，可能有不同的表述方法，在实际应用中可以灵活地选择．‎ 全称命题“”‎ 特称命题“”‎ 表述方法 对所有的成立 存在成立 对一切成立 至少有一个成立 对每一个成立 对有些成立 任选一个成立 对某个成立 凡，都有成立 有一个，使成立 ‎3．含有一个量词的命题的否定 全称命题的否定是特称命题，特称命题的否定是全称命题，如下所示：‎ 命题 命题的否定 ‎1．已知集合，，则中含有________________个元素．‎ ‎2．已知全集U={1，2，3，4，5，6}，集合P={1，3，5}，Q={1，2，4}，则=________________．‎ ‎3．设，集合是奇数集，集合是偶数集．若命题，，则________________．‎ ‎4．已知命题“”是假命题，则实数的取值范围是________________．‎ ‎5．若集合中只有一个元素，则________________．‎ ‎6．已知命题；命题若，则．则下列命题为假命题的是________________．‎ ‎①；②；③；④．‎ ‎7．命题甲：；命题乙：且，则甲是乙的________________条件．‎ ‎8．已知集合，集合，则以下命题正确的个数是________________．‎ ‎①；②；③；④．‎ ‎9．设，则“”是“”的________________条件．‎ ‎10．设集合，若，则的取值范围是________________．‎ ‎11．若“”是真命题，则实数m的最小值为________________．‎ ‎12．已知命题，命题，则中，是真命题的有________________个．‎ ‎（1）研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合，然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的意义．‎ ‎（2）空集是任何集合的子集，是任何非空集合的真子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解．求集合的子集(真子集)个数问题，当集合的元素个数较少时，常利用枚举法解决，枚举法不失为求集合的子集(真子集)个数的好方法，使用时应做到不重不漏．‎ ‎（3）利用集合元素的限制条件求参数的值或确定集合中的元素的个数时，要注意检验集合是否满足元素的互异性．对连续数集间的运算，借助数轴的直观性，进行合理转化；对已知连续数集间的关系，求其中参数的取值范围时，要注意单独考查等号能否取到．‎ ‎（4）由原命题写出其他三种命题，关键要分清原命题的条件和结论，将条件与结论互换即得逆命题，将条件与结论同时否定即得否命题，将条件与结论互换的同时进行否定即得逆否命题．原命题和逆否命题、逆命题和否命题有相同的真假性，解题时注意灵活应用．‎ ‎（5）给出一个命题，要判断它是真命题，需经过严格的推理证明；而要说明它是假命题，则只需举一反例即可．②由于原命题与其逆否命题为等价命题，有时可以利用这种等价性间接地证明命题的真假．‎ ‎（6）充分、必要条件的应用主要涉及根据充要条件求解参数的取值范围，求解参数的取值范围时，一定要注意区间端点值的检验，尤其是利用两个集合之间的关系求解参数的取值范围时，不等式是否能够取等号决定端点值的取舍，处理不当容易出现漏解或增解的现象．‎ ‎（7）命题的否定是直接对命题的结论进行否定；而否命题则是对原命题的条件和结论分别否定．不能混淆这两者的概念．‎ ‎（8）要确定一个全称命题是真命题，需保证该命题对所有的元素都成立；若能举出一个反例说明命题不成立，则该全称命题是假命题．要确定一个特称命题是真命题，举出一个例子说明该命题成立即可；若经过逻辑推理得到命题对所有的元素都不成立，则该特称命题是假命题．‎ ‎1．已知集合，则________________．‎ ‎2．命题“，使得”的否定形式是________________．‎ ‎3．已知集合，，定义，则集合的所有非空真子集的个数为________________．‎ ‎4．已知条件，条件，且是的充分不必要条件，则的取值范围是________________．‎ ‎5．若命题是真命题，则实数a的取值范围是________________．‎ ‎6．已知集合，且下列三个关系：①；②；③有且只有一个正确，则等于________________．‎ ‎7．已知是两条互相垂直的直线，是平面，则是的________________条件．‎ ‎8．已知函数，且给定条件“”，条件“”，若是的充分不必要条件，则实数的取值范围是________________．‎ ‎1．【答案】10‎ ‎【解析】列举得集合，‎ 该集合中共含有10个元素．‎ ‎【名师点睛】求解此类问题时，一定要注意代表元素的含义和集合的类型，是数集还是点集．‎ ‎4．【答案】‎ ‎【解析】当命题为真时，由且可得，故命题为假时，，‎ 故实数的取值范围是．‎ ‎5．【答案】4‎ ‎【解析】由题意得方程只有一个实数解，当时，方程无实数解；‎ 当时，则，解得(不符合题意，舍去)．‎ ‎6．【答案】①③④‎ ‎【解析】显然命题是真命题；‎ 命题若，则是假命题，所以是真命题，‎ 故，，为假命题．‎ ‎7．【答案】充分不必要 ‎【解析】因为是的充分不必要条件，所以命题甲：是命题乙：且的充分不必要条件．学！ ‎ ‎10．【答案】‎ ‎【解析】，∴，‎ 故的取值范围是．‎ ‎11．【答案】1‎ ‎【解析】若“”是真命题，则，‎ 其中，∵函数，的最大值为1，‎ ‎∴，即的最小值为1．‎ ‎12．【答案】‎ ‎【解析】∵，∴是假命题．‎ ‎∵存在，使，∴q是真命题，‎ 因此是真命题，¬p是真命题．‎ 真命题共有2个．‎ ‎1．【答案】[0，]‎ ‎【解析】由题意得，，，∴．‎ ‎2．【答案】，使得 ‎【解析】的否定是，的否定是，的否定是．‎ 故命题“，使得”的否定形式是“，使得”．‎ ‎3．【答案】30‎ ‎【解析】根据新定义的运算可知，的所有非空真子集的个数为．‎ ‎4．【答案】‎ ‎【解析】由条件，解得或；‎ 因为是的充分不必要条件，所以是的充分不必要条件，有，‎ 故的取值范围是．‎ ‎6．【答案】201‎ ‎【解析】可分下列三种情形：‎ ‎（1）若只有①正确，则a≠2，b≠2，c=0，所以a=b=1，与集合中元素的互异性相矛盾，所以只有①正确是不可能的；‎ ‎（2）若只有②正确，则b=2，a=2，c=0，这与集合中元素的互异性相矛盾，所以只有②正确是不可能的；（3）若只有③正确，则c≠0，a=2，b≠2，所以c=1，b=0，所以100a+10b+c=100×2+10×0+1=201．‎ ‎8．【答案】‎ ‎【解析】，‎ 当时，，则，所以，又当时，，若是的充分不必要条件，则，所以，故实数的取值范围是．‎ 个人总结 ‎________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________‎