- 1.24 MB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
空间向量(2)
【学习目标】
1.理解空间向量概念以及数量积等相关概念,会求法向量及向量所成的角;
2.明确线线角、线面角、面面角的范围并会求这些角.
【自主练习】 ]
1. 若向量a=(1,λ,2),b=(2,-1,2)且a与b的夹角的余弦值为,则λ=______.
2.由向量,所确定的平面的一个法向量为 .
3.如图,在平行六面体ABCDA1B1C1D1中,G为△A1BD的重心,设=a,=b,=c,试用a,b,c表示为__________
4.已知A(1,0,0),B(0,-1,1),向量+λ与向量的夹角为120°,则λ的值为 ________.
5.如图,正方体ABCDA1B1C1D1中,EF为异面直线A1D和AC的公垂线,则直线EF与BD1的位置关系是__________.
6. 已知直二面角αlβ,点Aα,AC⊥l,C为垂足,
Bβ,BD⊥l,D为垂足.若AB=2,AC=BD=1,
则D到平面ABC的距离等于________
答案:
【典型例题】
例1.如图所示的几何体是由以等边三角形为底面的棱柱被平面所截而得,已知平面,,,,,为的中点.
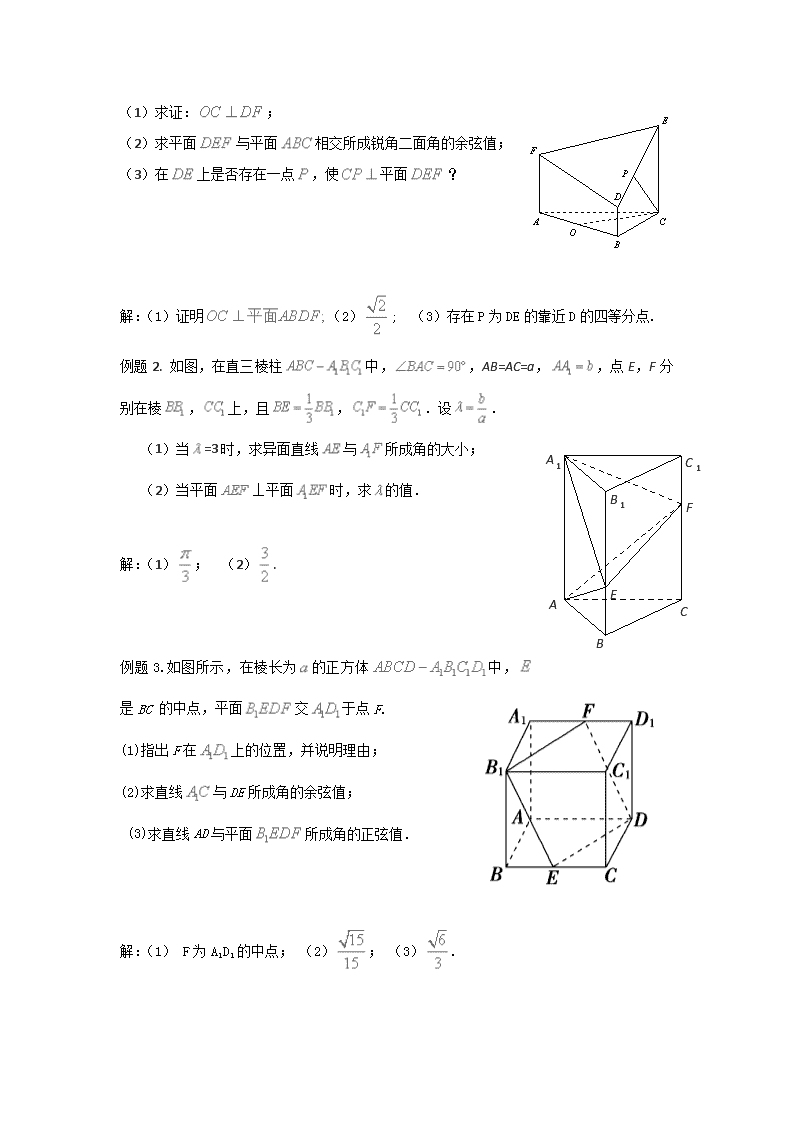
(1)求证:;
(2)求平面与平面相交所成锐角二面角的余弦值;
(3)在上是否存在一点,使平面?
解:(1)证明(2); (3)存在P为DE的靠近D的四等分点.
例题2. 如图,在直三棱柱中,,AB=AC=a,,点E,F分别在棱,上,且,.设.
F
E
C
1
B
1
A
1
C
B
A
(1)当=3时,求异面直线与所成角的大小;
(2)当平面⊥平面时,求的值.
解:(1); (2).
例题3.如图所示,在棱长为的正方体中,是BC的中点,平面交于点F.
(1)指出F在上的位置,并说明理由;
(2)求直线与DE所成角的余弦值;
(3)求直线AD与平面所成角的正弦值.
[来源: ]
[来源: ]
解:(1) F为A1D1的中点; (2); (3).
例题4.四棱锥P-ABCD的底面是边长为a的正方形,PA⊥底面ABCD,E是PC上的点,且CE:EP=1:2,
(1)在线段AB上是否存在点F,使得EF∥平面PAD?
(2)若二面角B-PC-D的大小是1200,求PA的长.
解:(1)存在F为AB上靠近B的一个三等分点;(2)