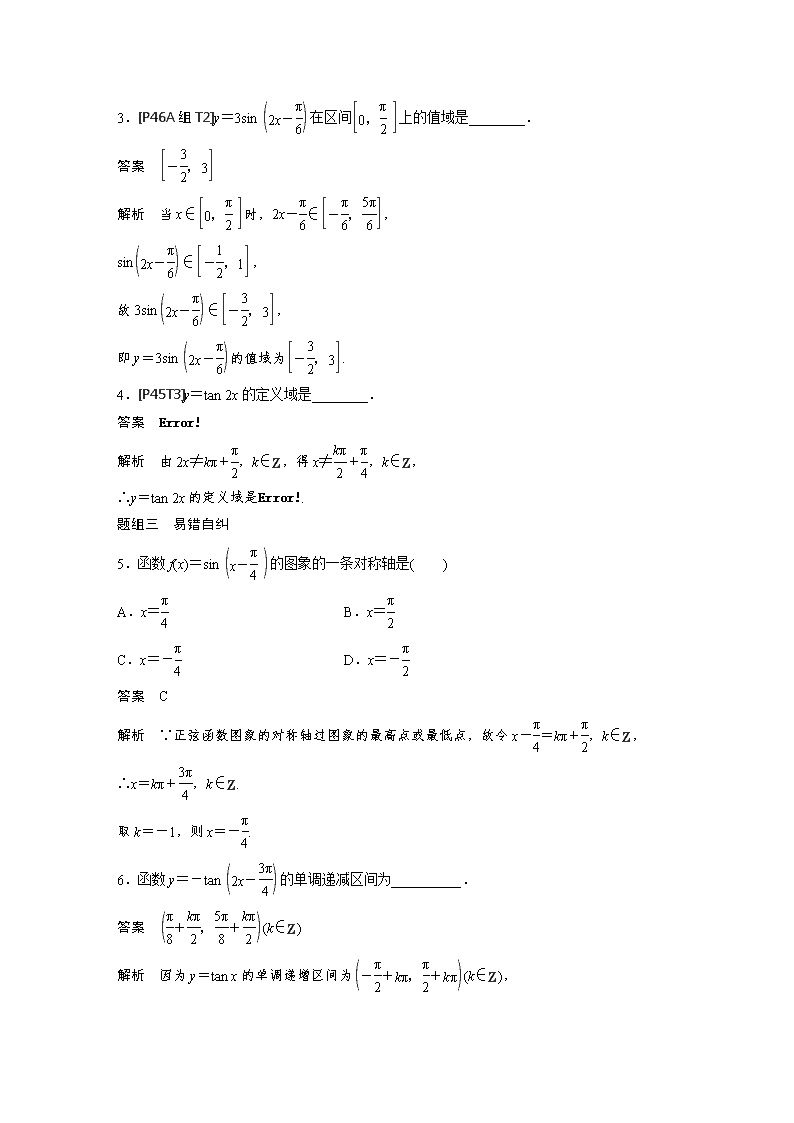【数学】2019届一轮复习北师大版4-3　三角函数的图象与性质学案 19页

‎§4.3　三角函数的图象与性质 最新考纲 考情考向分析 ‎1.能画出y＝sin x，y＝cos x，y＝tan x的图象，了解三角函数的周期性．‎ ‎2.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值，图象与x轴的交点等)，理解正切函数在区间内的单调性.‎ 以考查三角函数的图象和性质为主，题目涉及三角函数的图象及应用、图象的对称性、单调性、周期性、最值、零点．考查三角函数性质时，常与三角恒等变换结合，加强数形结合思想、函数与方程思想的应用意识．题型既有选择题和填空题，又有解答题，中档难度.‎ ‎　　　　　　　　　　　　　　　　　　　‎ ‎1．用五点法作正弦函数和余弦函数的简图 ‎(1)在正弦函数y＝sin x，x∈[0,2π]的图象中，五个关键点是：(0,0)，，(π，0)，，(2π，0)．‎ ‎(2)在余弦函数y＝cos x，x∈[0,2π]的图象中，五个关键点是：(0,1)，，(π，－1)，，(2π，1)．‎ ‎2．正弦、余弦、正切函数的图象与性质(下表中k∈Z)‎ 函数 y＝sin x y＝cos x y＝tan x 图象 定义域 R R x≠kπ＋}‎ 值域 ‎[－1,1]‎ ‎[－1,1]‎ R 周期性 ‎2π ‎2π π 奇偶性 奇函数 偶函数 奇函数 递增区间 ‎[2kπ－π，2kπ]‎ 递减区间 ‎[2kπ，2kπ＋π]‎ 无 对称中心 ‎(kπ，0)‎ 对称轴方程 x＝kπ＋ x＝kπ 无 知识拓展 ‎1．对称与周期 ‎(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是个周期．‎ ‎(2)正切曲线相邻两对称中心之间的距离是半个周期．‎ ‎2．奇偶性 若f(x)＝Asin(ωx＋φ)(A，ω≠0)，则：‎ ‎(1)f(x)为偶函数的充要条件是φ＝＋kπ(k∈Z)；‎ ‎(2)f(x)为奇函数的充要条件是φ＝kπ(k∈Z)．‎ 题组一　思考辨析 ‎1．判断下列结论是否正确(请在括号中打“√”或“×”)‎ ‎(1)y＝sin x在第一、第四象限上是增函数．(　×　)‎ ‎(2)由sin＝sin知，是正弦函数y＝sin x(x∈R)的一个周期．(　×　)‎ ‎(3)正切函数y＝tan x在定义域内是增函数．(　×　)‎ ‎(4)已知y＝ksin x＋1，x∈R，则y的最大值为k＋1.(　×　)‎ ‎(5)y＝sin|x|是偶函数．(　√　)‎ 题组二　教材改编 ‎2．[P35例2]函数f(x)＝cos的最小正周期是________．‎ 答案　π ‎3．[P46A组T2]y＝3sin在区间上的值域是________．‎ 答案　 解析　当x∈时，2x－∈，‎ sin∈，‎ 故3sin∈，‎ 即y＝3sin的值域为.‎ ‎4．[P45T3]y＝tan 2x的定义域是________．‎ 答案　 解析　由2x≠kπ＋，k∈Z，得x≠＋，k∈Z，‎ ‎∴y＝tan 2x的定义域是.‎ 题组三　易错自纠 ‎5．函数f(x)＝sin的图象的一条对称轴是(　　)‎ A．x＝ B．x＝ C．x＝－ D．x＝－ 答案　C 解析　∵正弦函数图象的对称轴过图象的最高点或最低点，故令x－＝kπ＋，k∈Z，‎ ‎∴x＝kπ＋，k∈Z.‎ 取k＝－1，则x＝－.‎ ‎6．函数y＝－tan的单调递减区间为__________．‎ 答案　(k∈Z)‎ 解析　因为y＝tan x的单调递增区间为(k∈Z)，‎ 所以由－＋kπ<2x－<＋kπ，k∈Z，‎ 得＋cos 23°>cos 97°‎ 解析　sin 68°＝cos 22°，‎ 又y＝cos x在[0°，180°]上是减函数，‎ ‎∴sin 68°>cos 23°>cos 97°.‎ 题型一　三角函数的定义域和值域 ‎1．函数f(x)＝－2tan的定义域是(　　)‎ A. B. C. D. 答案　D 解析　由正切函数的定义域，得2x＋≠kπ＋，k∈Z，即x≠＋(k∈Z)，故选D.‎ ‎2．函数y＝的定义域为________．‎ 答案　(k∈Z)‎ 解析　方法一　要使函数有意义，必须使sin x－cos x≥0.利用图象，在同一坐标系中画出[0,2π]上y＝sin x和y＝cos x的图象，如图所示．在[0,2π]内，满足sin x＝cos x的x为，，再结合正弦、余弦函数的周期是2π，所以原函数的定义域为.‎ 方法二　利用三角函数线，画出满足条件的终边范围(如图阴影部分所示)．所以定义域为 .‎ ‎3．函数y＝－2sin x－1，x∈的值域是________．‎ 答案　(－2,1]‎ 解析　当x∈时，－1≤sin x<，‎ 所以函数y＝－2sin x－1，x∈的值域是(－2,1]．‎ ‎4．(2018届山东邹平双语学校月考)函数f(x)＝sin2x＋cos x－的最大值是________．‎ 答案　1‎ 解析　f(x)＝sin2x＋cos x－ ‎＝1－cos2x＋cos x－，‎ 令cos x＝t且t∈[0,1]，‎ 则y＝－t2＋t＋＝－2＋1，‎ 当t＝时，ymax＝1，‎ 即f(x)的最大值是1.‎ 思维升华 (1)三角函数定义域的求法 求三角函数的定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．‎ ‎(2)三角函数值域的不同求法 ‎①利用sin x和cos x的值域直接求；‎ ‎②把所给的三角函数式变换成y＝Asin(ωx＋φ)(A，ω≠0)的形式求值域；‎ ‎③通过换元，转换成二次函数求值域．‎ 题型二　三角函数的单调性 命题点1　求三角函数的单调性 典例 (1)函数f(x)＝tan的单调递增区间是(　　)‎ A.(k∈Z)‎ B.(k∈Z)‎ C.(k∈Z)‎ D.(k∈Z)‎ 答案　B 解析　由kπ－＜2x－＜kπ＋(k∈Z)，‎ 得－＜x＜＋(k∈Z)，‎ 所以函数f(x)＝tan的单调递增区间为 (k∈Z)，故选B.‎ ‎(2)(2017·哈尔滨、长春、沈阳、大连四市联考)函数y＝sin x＋cos x的单调递增区间是____________．‎ 答案　 解析　∵y＝sin x＋cos x＝sin，‎ 由2kπ－≤x＋≤2kπ＋(k∈Z)，‎ 解得2kπ－≤x≤2kπ＋(k∈Z)．‎ ‎∴函数的单调递增区间为(k∈Z)，‎ 又x∈，∴单调递增区间为.‎ 命题点2　根据单调性求参数 典例 已知ω＞0，函数f(x)＝sin在上单调递减，则ω的取值范围是________．‎ 答案　 解析　由＜x＜π，ω＞0，得 ＋＜ωx＋＜ωπ＋，‎ 又y＝sin x的单调递减区间为，k∈Z，‎ 所以k∈Z，‎ 解得4k＋≤ω≤2k＋，k∈Z.‎ 又由4k＋－≤0，k∈Z且2k＋>0，k∈Z，得k＝0，所以ω∈.‎ 引申探究 本例中，若已知ω>0，函数f(x)＝cos在上单调递增，则ω的取值范围是______．‎ 答案　 解析　函数y＝cos x的单调递增区间为[－π＋2kπ，2kπ]，k∈Z，‎ 则k∈Z，‎ 解得4k－≤ω≤2k－，k∈Z，‎ 又由4k－－≤0，k∈Z且2k－＞0，k∈Z，‎ 得k＝1，所以ω∈.‎ 思维升华 (1)已知三角函数解析式求单调区间 求形如y＝Asin(ωx＋φ)或y＝Acos(ωx＋φ)(其中ω＞0)的单调区间时，要视“ωx＋φ”为一个整体，通过解不等式求解．但如果ω＜0，可借助诱导公式将ω化为正数，防止把单调性弄错．‎ ‎(2)已知三角函数的单调区间求参数．先求出函数的单调区间，然后利用集合间的关系求解．‎ 跟踪训练　(2017·济南模拟)若函数f(x)＝sin ωx(ω>0)在区间上单调递增，在区间上单调递减，则ω等于(　　)‎ A. B. C．2 D．3‎ 答案　B 解析　由已知得＝，‎ ‎∴T＝，∴ω＝＝.‎ 题型三　三角函数的周期性、奇偶性、对称性 命题点1　三角函数的周期性 典例 (1)(2017·湘西自治州模拟)已知函数f(x)＝sin(ωx－ωπ)(ω>0)的最小正周期为π，则f等于(　　)‎ A. B．－ C. D．－ 答案　A 解析　∵T＝π，∴ω＝＝＝2，‎ ‎∴f(x)＝sin＝sin 2x，‎ ‎∴f＝sin ＝.‎ ‎(2)若函数f(x)＝2tan的最小正周期T满足10，ω>0)．若f(x)在区间上具有单调性，且f＝f＝－f，则f(x)的最小正周期为________．‎ 解析　记f(x)的最小正周期为T.‎ 由题意知≥－＝，‎ 又f＝f＝－f，‎ 且－＝，‎ 可作出示意图如图所示(一种情况)：‎ ‎∴x1＝×＝，x2＝×＝，‎ ‎∴＝x2－x1＝－＝，∴T＝π.‎ 答案　π ‎1．(2017·广州五校联考)下列函数中，周期为π的奇函数为(　　)‎ A．y＝sin xcos x B．y＝sin2x C．y＝tan 2x D．y＝sin 2x＋cos 2x 答案　A 解析　y＝sin xcos x＝sin 2x，‎ 周期为π，且是奇函数．‎ ‎2．函数f(x)＝sin在区间上的最小值为(　　)‎ A．－1 B．－ C. D．0‎ 答案　B 解析　由已知x∈，得2x－∈，‎ 所以sin∈，‎ 故函数f(x)＝sin在区间上的最小值为－.故选B.‎ ‎3．函数y＝sin x2的图象是(　　)‎ 答案　D 解析　函数y＝sin x2为偶函数，排除A，C；又当x＝时函数取得最大值，排除B，故选D.‎ ‎4．(2017·成都诊断)函数y＝cos2x－2sin x的最大值与最小值分别为(　　)‎ A．3，－1 B．3，－2 C．2，－1 D．2，－2‎ 答案　D 解析　y＝cos2x－2sin x＝1－sin2x－2sin x ‎＝－sin2x－2sin x＋1，‎ 令t＝sin x，‎ 则t∈[－1,1]，y＝－t2－2t＋1＝－(t＋1)2＋2，‎ 所以ymax＝2，ymin＝－2.‎ ‎5．已知函数f(x)＝2sin(2x＋φ)的图象过点(0，)，则f(x)图象的一个对称中心是(　　)‎ A. B. C. D. 答案　B 解析　函数f(x)＝2sin(2x＋φ)的图象过点(0，)，则f(0)＝2sin φ＝，‎ ‎∴sin φ＝，又|φ|<，∴φ＝，‎ 则f(x)＝2sin，令2x＋＝kπ(k∈Z)，‎ 则x＝－(k∈Z)，当k＝0时，x＝－，‎ ‎∴是函数f(x)的图象的一个对称中心．‎ ‎6．已知函数f(x)＝－2sin(2x＋φ)(|φ|<π)，若f＝－2，则f(x)的一个单调递减区间是(　　)‎ A. B. C. D. 答案　C 解析　由f＝－2，得 f＝－2sin＝－2sin＝－2，‎ 所以sin＝1.‎ 因为|φ|<π，所以φ＝.‎ 由2kπ－≤2x＋≤2kπ＋，k∈Z，‎ 解得kπ－≤x≤kπ＋，k∈Z.‎ 当k＝0时，－≤x≤，故选C.‎ ‎7．函数y＝cos的单调递减区间为__________．‎ 答案　(k∈Z)‎ 解析　因为y＝cos＝cos，‎ 所以令2kπ≤2x－≤2kπ＋π(k∈Z)，‎ 解得kπ＋≤x≤kπ＋(k∈Z)，‎ 所以函数的单调递减区间为(k∈Z)．‎ ‎8．(2018·福州质检)函数y＝cos2x＋sin x的最小值为____________．‎ 答案　 解析　令t＝sin x，∵|x|≤，∴t∈.‎ ‎∴y＝－t2＋t＋1＝－2＋，‎ ‎∴当t＝－时，ymin＝.‎ ‎9．已知函数f(x)＝2sin＋1(x∈R)的图象的一条对称轴为x＝π，其中ω为常数，且ω∈(1,2)，则函数f(x)的最小正周期为________．‎ 答案　 解析　由函数f(x)＝2sin＋1(x∈R)的图象的一条对称轴为x＝π，可得ωπ－＝kπ＋，k∈Z，‎ ‎∴ω＝k＋，又ω∈(1,2)，∴ω＝，‎ 从而得函数f(x)的最小正周期为＝.‎ ‎10．(2018·珠海模拟)设函数f(x)＝3sin，若存在这样的实数x1，x2，对任意的x∈R，都有f(x1)≤f(x)≤f(x2)成立，则|x1－x2|的最小值为________．‎ 答案　2‎ 解析　|x1－x2|的最小值为函数f(x)的半个周期，‎ 又T＝4，∴|x1－x2|的最小值为2.‎ ‎11．已知f(x)＝sin.‎ ‎(1)求函数f(x)图象的对称轴方程；‎ ‎(2)求f(x)的单调递增区间；‎ ‎(3)当x∈时，求函数f(x)的最大值和最小值．‎ 解　(1)f(x)＝sin，‎ 令2x＋＝kπ＋，k∈Z，‎ 得x＝＋，k∈Z.‎ 所以函数f(x)图象的对称轴方程是x＝＋，k∈Z.‎ ‎(2)令2kπ－≤2x＋≤2kπ＋，k∈Z，‎ 得kπ－≤x≤kπ＋，k∈Z.‎ 故f(x)的单调递增区间为，k∈Z.‎ ‎(3)当x∈时，≤2x＋≤，‎ 所以－1≤sin≤，‎ 所以－≤f(x)≤1，‎ 所以当x∈时，函数f(x)的最大值为1，最小值为－.‎ ‎12. (2017·武汉调研)已知函数f(x)＝a＋b.‎ ‎(1)若a＝－1，求函数f(x)的单调增区间；‎ ‎(2)当x∈[0，π]时，函数f(x)的值域是[5,8]，求a，b的值．‎ 解　f(x)＝a(1＋cos x＋sin x)＋b ‎＝asin＋a＋b.‎ ‎(1)当a＝－1时，f(x)＝－sin＋b－1，‎ 由2kπ＋≤x＋≤2kπ＋(k∈Z)，‎ 得2kπ＋≤x≤2kπ＋(k∈Z)，‎ ‎∴f(x)的单调增区间为(k∈Z)．‎ ‎(2)∵0≤x≤π，∴≤x＋≤，‎ ‎∴－≤sin≤1.依题意知a≠0，‎ ‎①当a>0时，∴a＝3－3，b＝5；‎ ‎②当a<0时，∴a＝3－3，b＝8.‎ 综上所述，a＝3－3，b＝5或a＝3－3，b＝8.‎ ‎13．(2018·广州质检)已知函数f(x)＝2sin ωx(ω>0)在区间上的最小值是－2，则ω的最小值等于(　　)‎ A. B. C．2 D．3‎ 答案　B 解析　∵ω>0，－≤x≤，∴－≤ωx≤.‎ 由已知条件知－≤－或≥，‎ ‎∴ω≥.∴ω的最小值为.‎ ‎14．已知关于x的方程2sin＋1－a＝0在区间上存在两个根，则实数a的取值范围是________．‎ 答案　[2,3)‎ 解析　sin＝在上存在两个根，设x＋＝t，则t∈，‎ ‎∴y＝sin t，t∈的图象与直线y＝有两个交点，∴≤<1，∴2≤a<3.‎ ‎15．已知函数f(x)＝2cos(ωx＋φ)＋b对任意实数x有f＝f(－x)恒成立，且f＝1，则实数b的值为(　　)‎ A．－1 B．3 C．－1或3 D．－3‎ 答案　C 解析　由f＝f(－x)可知函数f(x)＝2cos(ωx＋φ)＋b关于直线x＝对称，又函数f(x)在对称轴处取得最值，故±2＋b＝1，∴b＝－1或b＝3.‎ ‎16．已知f(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<)的最小正周期为2，且当x＝时，f(x)的最大值为2.‎ ‎(1)求f(x)的解析式；‎ ‎(2)在闭区间上是否存在m，使x＝m是函数f(x)的对称轴？如果存在，求出m；如果不存在，请说明理由．‎ 解　(1)由已知得＝2，∴ω＝π，‎ ‎∵f(x)的最大值为2，∴A＝2.‎ 又A＝2，且f＝2sin＝2，‎ ‎∴＋φ＝2kπ＋(k∈Z)，‎ ‎∴φ＝2kπ＋，k∈Z，又|φ|<，∴φ＝.‎ ‎∴f(x)＝2sin.‎ ‎(2)由πx＋＝kπ＋，得x＝k＋(k∈Z), ‎ 即函数f(x)的对称轴为x＝k＋(k∈Z)．‎ 由≤k＋≤，‎ 得≤k≤，又k∈Z，‎ ‎∴k＝5，此时的对称轴为x＝，‎ 故在闭区间上存在实数m＝，使x＝m是函数f(x)的对称轴．‎