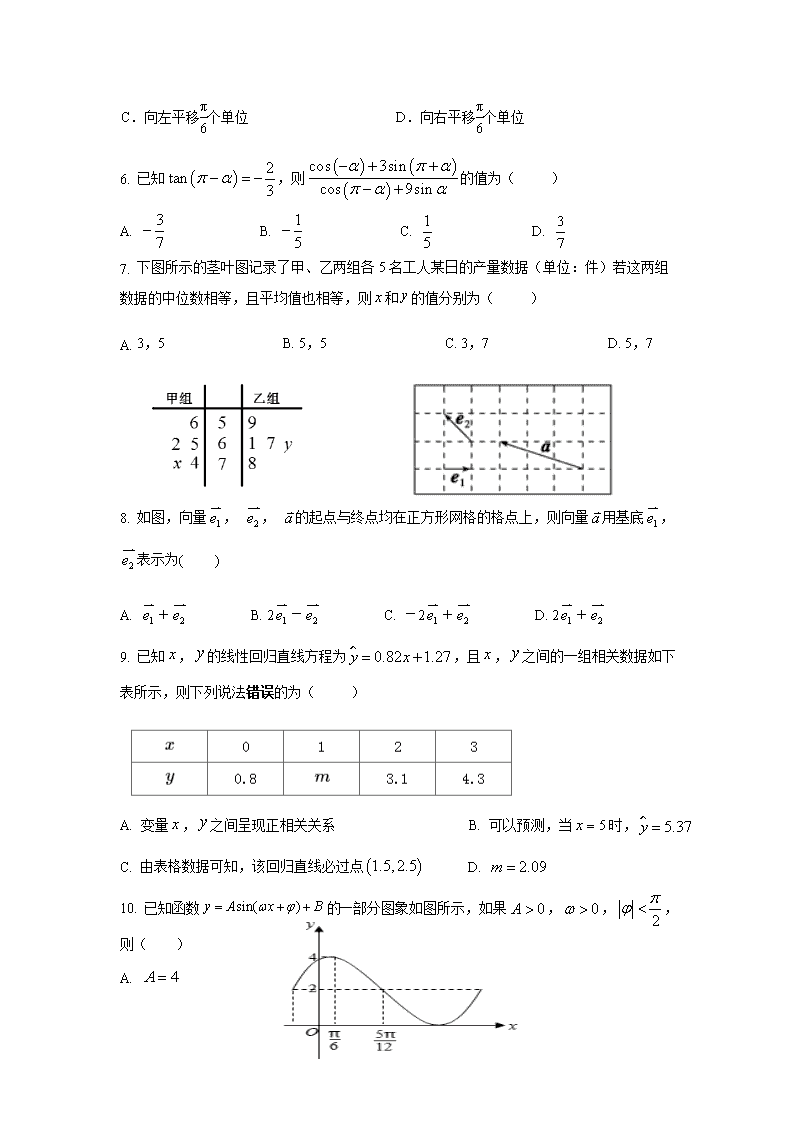
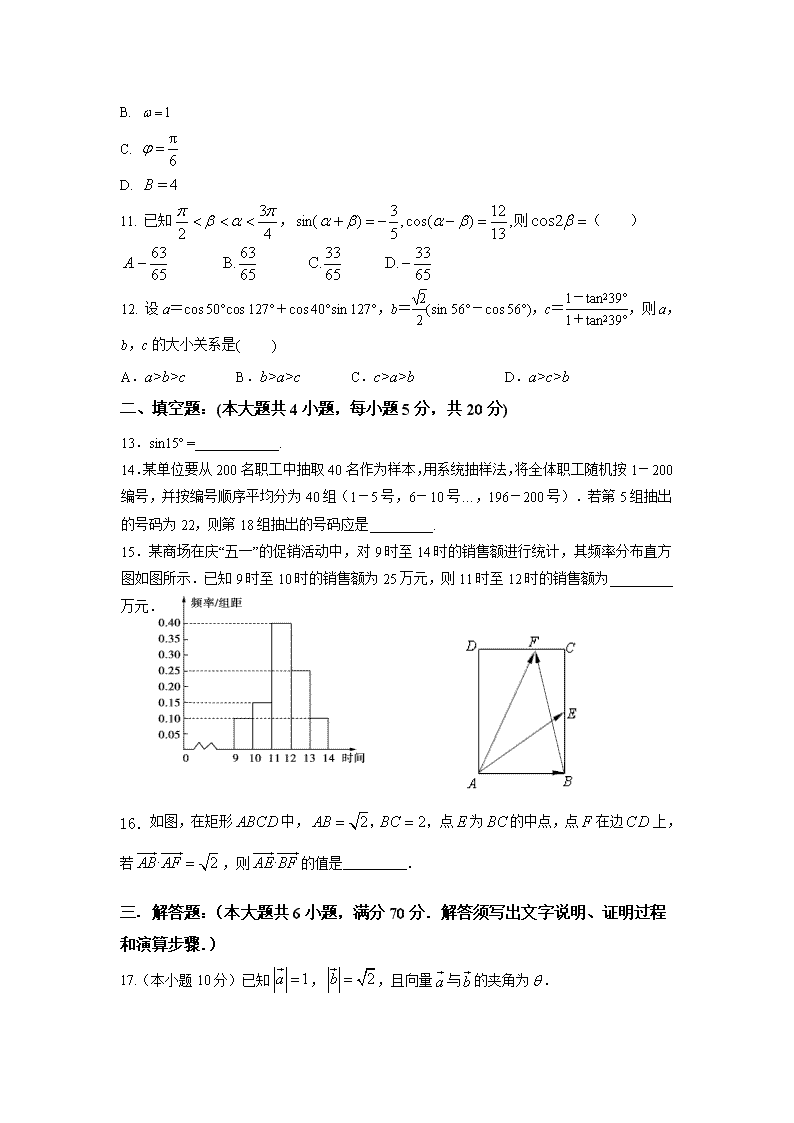
- 602.50 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
湛江市第二十一中学高一年级复学教学质量检测
数 学 试 卷
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.考试时间120分钟,满分150分.
第Ⅰ卷(选择题,共60分)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 已知点在第三象限,则角的终边在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知向量,,且,则的值为( )
A. B. C. D.
3. 函数的图象的一条对称轴方程是( )
A. B. C. D.
4. 下列各式中,值为的是( )
A. B. C. D.
5. 要得到函数的图象,只需将函数y=sin 2x的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
6. 已知,则的值为( )
A. B. C. D.
7. 下图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件)若这两组数据的中位数相等,且平均值也相等,则和的值分别为( )
A. 3,5 B. 5,5 C. 3,7 D. 5,7
8. 如图,向量, , 的起点与终点均在正方形网格的格点上,则向量用基底, 表示为( )
A. + B. 2- C. -2+ D. 2+
9. 已知,的线性回归直线方程为,且,之间的一组相关数据如下表所示,则下列说法错误的为( )
A. 变量,之间呈现正相关关系 B. 可以预测,当时,
C. 由表格数据可知,该回归直线必过点 D.
10. 已知函数一部分图象如图所示,如果,,,则( )
A.
B.
C.
D.
11. 已知,则( )
12. 设a=cos 50°cos 127°+cos 40°sin 127°,b=(sin 56°-cos 56°),c=,则a,b,c的大小关系是( )
A.a>b>c B.b>a>c C.c>a>b D.a>c>b
二、填空题:(本大题共4小题,每小题5分,共20分)
13.sin15º =____________.
14.某单位要从200名职工中抽取40名作为样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第18组抽出的号码应是_________.
15.某商场在庆“五一”的促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为25万元,则11时至12时的销售额为_________万元.
16. 如图,在矩形中,点为的中点,点在边上,若,则的值是 .
三.解答题:(本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.)
17.(本小题10分)已知,,且向量与的夹角为.
(1)若,求; (2)若与垂直,求.
18.(本小题12分)已知函数的最小正周期为,且该函数图象上的最低点的纵坐标为.
(1)求函数的解析式; (2)求函数的单调递增区间及对称轴方程.
19. (本小题12分)已知函数(R).
(1) 求的最小正周期和最大值; (2)若为锐角,且,求的值.
20. (本小题12分)某出租车公司购买了140辆纯电动汽车作为运营车辆,目前我国纯电动汽车按续航里程数R(单位:千米)分为3类,即A类:80≤R<150,B类:150≤R<250,C类:R≥250.该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型
A类
B类
C类
已行驶总里程不超过10万千米的车辆数
10
40
30
已行驶总里程超过10万千米的车辆数
20
20
20
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万千米的概率;
(2)公司为了了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从C类车中抽取了n辆车.
①求n的值; ②如果从这n辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万千米的概率.
21.(本小题12分)在某化学反应的中间阶段,压力保持不变,温度从1°变化到5°,反应结果如下表所示(x代表温度,代表结果):
(1)求化学反应的结果对温度的线性回归方程;
(2)判断变量与之间是正相关还是负相关,并预测当温度达到10°时反应结果为多少?
附::线性回归方程中,
22.(本小题12分)如图,A是单位圆与x轴正半轴的交点,点B、P在单位圆上,且B,,(),,设四边形OAQP的面积为S.
(1)求;
(2)令=,求的单调递增区间.
湛江市第二十一中学高一年级教学质量检测
数学参考答案
一、 选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
A
B
D
B
A
C
C
D
A
D
二、填空题:
12. 14. 87 15. 100 16.
三、解答题:
17.解:(1)因,所以
(2)因为与垂直,所以,即,
所以,又,所以
18.解:(1)因为的最小正周期为,,,∴.
又函数图象上的最低点纵坐标为,且,∴
∴.
(2)由,可得
可得单调递增区间.
由,得.
所以函数的对称轴方程为.
19.(1) 解:
∴的最小正周期为, 最大值为
(2) 解:∵, ∴ ∴
∵为锐角,即, ∴. ∴.
∴
19. 解:(1)从这140辆汽车中任取一辆,则该车行驶总里程超过10万千米的概率为
P1==.
(2) ①依题意n=×14=5.
②5辆车中已行驶总里程不超过10万千米的车有3辆,记为a,b,c;
5辆车中已行驶总里程超过10万千米的车有2辆,记为m,n.
“从5辆车中随机选取两辆车”的所有选法共10种:
ab,ac,am,an,bc,bm,bn,cm,cn,mn.“
从5辆车中随机选取两辆车,恰有一辆车行驶里程超过10万千米”的选法共6种:
am,an,bm,bn,cm,cn,
则选取两辆车中恰有一辆车行驶里程超过10万千米的概率P2==.
21.解:(1)由题意:,,,
又,
∴,,
故所求的回归方程为
(2)由于变量的值随温度的值增加而增加,故与之间是正相关.
当时,
22.解: