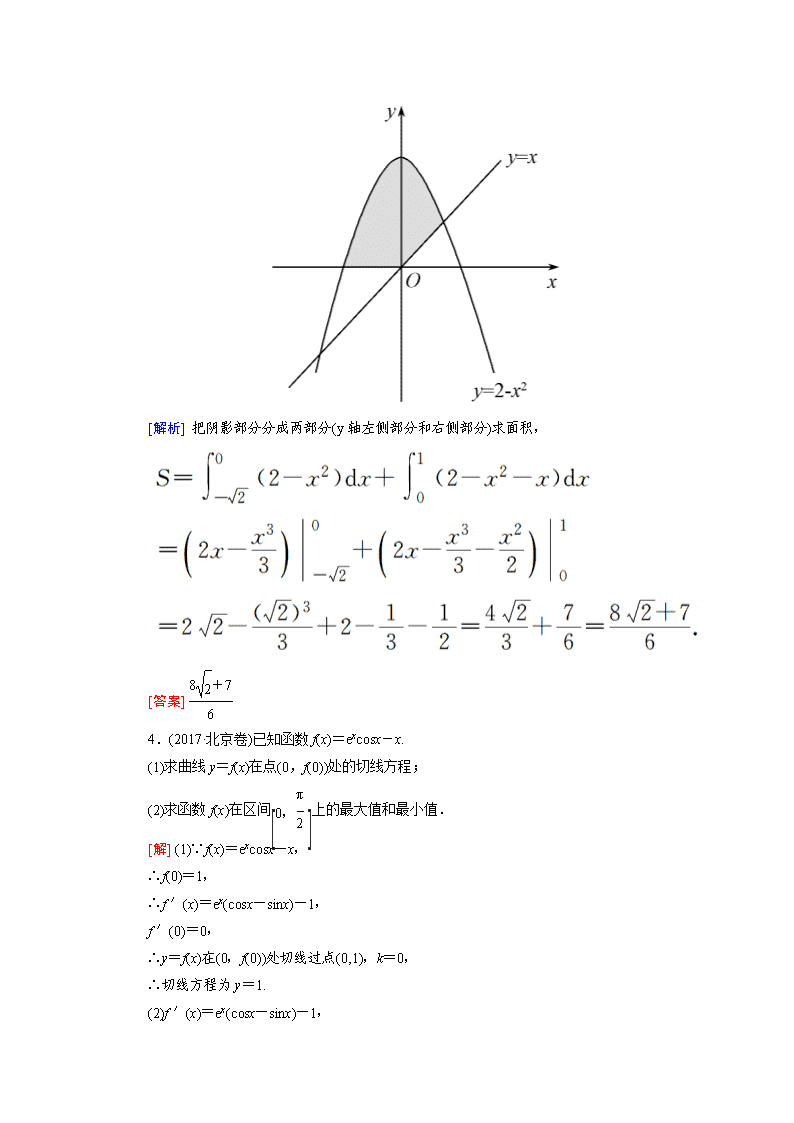【数学】2019届一轮复习北师大版导数的简单应用学案 14页

专题一 集合、常用逻辑用语、不等式、函数与导数 第五讲 导数的简单应用 高考导航 导数的意义和运算是导数应用的基础，是高考的一个热点．‎ ‎2．利用函数的单调性和最值确定函数的解析式或参数的值，突出考查导数的工具性作用.‎ ‎1．(2017·福州质检)函数f(x)＝x3－ax为R上增函数的一个充分不必要条件是( )‎ A．a≤0 B．a<0 C．a≥0 D．a>0‎ ‎[解析] 函数f(x)＝x3－ax为R上增函数的一个充分不必要条件是f ′(x)＝3x2－a>0在R上恒成立，所以a<(3x2)min.因为(3x2)min＝0，所以a<0.故选B.‎ ‎[答案] B ‎2．(2017·全国卷Ⅱ)若x＝－2是函数f(x)＝(x2＋ax－1)ex－1的极值点，则f(x)的极小值为( )‎ A．－1 B．－2e－3 C．5e－3 D．1‎ ‎[解析] 由题意可得f′(x)＝ex－1[x2＋(a＋2)x＋a－1]．‎ ‎∵x＝－2是函数f(x)＝(x2＋ax－1)ex－1的极值点，‎ ‎∴f ′(－2)＝0，∴a＝－1，∴f(x)＝(x2－x－1)ex－1，f ′(x)＝ex－1(x2＋x－2)＝ex－1(x－1)(x＋2)，‎ ‎∴x∈(－∞，－2)，(1，＋∞)时，f ′(x)>0，f(x)单调递增；x∈(－2,1)时，f ′(x)<0，f(x)单调递减．‎ ‎∴f(x)极小值＝f(1)＝－1.故选A.‎ ‎[答案] A ‎3．(2017·衡水中学三模)由曲线y＝2－x2，直线y＝x及x轴所围成的封闭图形(图中的阴影部分)的面积是________．‎ ‎[解析] 把阴影部分分成两部分(y轴左侧部分和右侧部分)求面积，‎ ‎[答案] ‎4．(2017·北京卷)已知函数f(x)＝excosx－x.‎ ‎(1)求曲线y＝f(x)在点(0，f(0))处的切线方程；‎ ‎(2)求函数f(x)在区间上的最大值和最小值．‎ ‎[解] (1)∵f(x)＝excosx－x，‎ ‎∴f(0)＝1，‎ ‎∴f ′(x)＝ex(cosx－sinx)－1，‎ f ′(0)＝0，‎ ‎∴y＝f(x)在(0，f(0))处切线过点(0,1)，k＝0，‎ ‎∴切线方程为y＝1.‎ ‎(2)f ′(x)＝ex(cosx－sinx)－1，‎ 设f ′(x)＝g(x)，‎ ‎∴g′(x)＝－2sinx·ex≤0，‎ ‎∴g(x)在上单调递减，‎ ‎∴g(x)≤g(0)＝0，∴f′(x)≤0，‎ ‎∴f(x)在上单调递减，‎ ‎∴f(x)max＝f(0)＝1，‎ f(x)min＝f＝－.‎ 考点一 导数的几何意义与定积分 ‎1．导数公式 ‎(1)(sinx)′＝cosx；‎ ‎(2)(cosx)′＝－sinx；‎ ‎(3)(ax)′＝axlna(a>0)；‎ ‎(4)(logax)′＝(a>0，且a≠1)．‎ ‎2．导数的几何意义 函数f(x)在x0处的导数是曲线f(x)在点P(x0，f(x0))处的切线的斜率，曲线f(x)在点P处的切线的斜率k＝f ′(x0)，相应的切线方程为y－f(x0)＝f ′(x0)·(x－x0)．‎ ‎3．微积分基本定理 一般地，如果f(x)是区间[a，b]上的连续函数，并且F′(x)＝f(x)，那么f(x)dx＝F(b)－F(a)．‎ ‎[对点训练]‎ ‎1．(2017·大同模拟)过点(1，－1)且与曲线y＝x3－2x相切的切线方程为( )‎ A．x－y－2＝0或5x＋4y－1＝0‎ B．x－y－2＝0‎ C．x－y＋2＝0‎ D．x－y－2＝0或4x＋5y＋1＝0‎ ‎[解析] 设切点坐标为(x0，y0)，y0＝x－2x0，则曲线在(x0，y0)处的切线斜率为y′＝3x－2，当x0＝1时斜率为1，切线方程为x－y－2＝0，当x0≠1时，过(1，－1)点的切线的斜率为＝x＋x0－1＝3x－2，解得x0＝－，其斜率为－，切线方程为5x＋4y－1＝0，所以A正确．‎ ‎[答案] A ‎2．(2017·北京卷改编)已知函数f(x)＝excosx－x.则曲线y＝f(x)在点(0，f(0))处的切线方程为_________________________．‎ ‎[解析] 因为f(x)＝excosx－x，所以f ′(x)＝ex(cosx－sinx)－1，f ′(0)＝0.‎ 又f(0)＝1，所以曲线y＝f(x)在点(0, f(0))处的切线方程为y＝1.‎ ‎[答案] y＝1‎ ‎3．(2017·安徽示范高中二模)计算：(－x)dx＝________.‎ ‎[解析] 由定积分的几何意义知dx是由y＝与直线x＝0，x＝1所围成的图形的面积，即是以(1,0)为圆心，以1为半径的圆的面积的，故dx＝，(－x)dx＝－x2＝－，‎ ‎∴－x)dx＝.‎ ‎[答案] ‎4．(2017·宁夏二模)曲线y＝x2和直线x＝0，x＝1，y＝所围成的图形(如图中阴影部分所示)的面积为________．‎ ‎ [解析] 令x2＝，得x＝或x＝－(舍去)，所以所 ‎[答案] ‎(1)求曲线y＝f(x)的切线方程的3种类型及方法 ‎①已知切点P(x0，y0)，求y＝f(x)过点P的切线方程：‎ 求出切线的斜率f′(x0)，由点斜式写出方程．‎ ‎②已知切线的斜率为k，求y＝f(x)的切线方程：设切点P(x0，y0)，通过方程k＝f′(x0)解得x0，再由点斜式写出方程．‎ ‎③已知切线上一点(非切点)，求y＝f(x)的切线方程：‎ 设切点P(x0，y0)，利用导数求得切线斜率f′(x0)，然后由斜率公式求得切线斜率，列方程(组)解得x0，再由点斜式或两点式写出方程．‎ ‎(2)求定积分的2种方法 ‎①利用微积分基本定理求定积分；‎ ‎②利用定积分的几何意义求定积分．‎ ‎【易错提醒】 求曲线的切线方程时，务必分清点P处的切线还是过点P的切线，前者点P为切点，后者点P不一定为切点，求解时应先求出切点坐标．‎ 考点二 利用导数研究函数的单调性 ‎1．若求函数的单调区间(或证明单调性)，只要在其定义域内解(或证明)不等式f ′(x)>0或f ′(x)<0即可．‎ ‎2．若已知函数的单调性，则转化为不等式f ′(x)≥0或f ′(x)≤0在单调区间上恒成立问题来求解．角度1：根据函数的单调性，利用导数求某些参数的取值范围 A．(－∞，2] B．(－∞，4] ‎ C．(－∞，8] D．[－2,4]‎ ‎[解析] f′(x)＝[x2＋(2－c)x－c＋5]ex，∵函数f(x)在区间上单调递增，等价于x2‎ ‎＋(2－c)x－c＋5≥0对任意x∈恒成立，即(x＋1)c≤x2＋2x＋5，‎ ‎∴c≤对任意x∈恒成立，‎ ‎∵x∈，∴＝(x＋1)＋≥4，当且仅当x＝1时等号成立，∴c≤4.‎ ‎[答案] B ‎[探究追问] 例1－1中若f(x)＝(x2－cx＋5)ex在上存在减区间，则实数c的取值范围是________．‎ ‎[解析] f′(x)＝[x2＋(2－c)x－c＋5]ex，∵函数f(x)在上存在减区间，所以f ′(x)<0在上有解，即x2＋(2－c)x－c＋5<0在上有解，得c>在上有解．‎ ‎∵x∈，∴＝(x＋1)＋的最小值为4，∴c>4.‎ ‎[答案] (4，＋∞)‎ 角度2：利用函数的单调性与导数的关系，讨论含有参数的较复杂基本函数的单调性 ‎[思维流程] →→ ‎[解] f(x)的定义域为(0，＋∞)，‎ f′(x)＝a－－＋＝.‎ 当a≤0时，x∈(0,1)时，f′(x)>0，f(x)单调递增，‎ x∈(1，＋∞)时，f′(x)<0，f(x)单调递减．‎ 当a>0时，‎ f′(x)＝.‎ ‎(1)01，‎ 当x∈(0,1)或x∈时，f′(x)>0，f(x)单调递增，‎ 当x∈时，f′(x)<0，f(x)单调递减．‎ ‎(2)a＝2时，＝1，在x∈(0，＋∞)内，f′(x)≥0，f(x)单调递增．‎ ‎(3)a>2时，0<<1，‎ 当x∈或x∈(1，＋∞)时，f′(x)>0，f(x)单调递增，‎ 当x∈时，f′(x)<0，f(x)单调递减．‎ 综上所述，当a≤0时，f(x)在(0,1)内单调递增，在(1，＋∞)内单调递减；‎ 当02时，f(x)在内单调递增，在内单调递减，在(1，＋∞)内单调递增．‎ ‎ 利用导数研究函数单调性的3个关注点 ‎(1)利用导数研究函数的单调性，大多数情况下归结为对含有参数的不等式的解集的讨论．‎ ‎(2)在能够通过因式分解求出不等式对应方程的根时，依据根的大小进行分类讨论．‎ ‎(3)在不能通过因式分解求出根时，根据一元二次不等式对应方程的判别式或特殊值进行分类讨论．‎ ‎ [对点训练]‎ ‎1．[角度1]若函数f(x)＝x＋－mlnx在[1,2]上为减函数，则m的最小值为( )‎ A. B. C. D. ‎[解析] 因为f(x)＝x＋－mlnx在[1,2]上为减函数，所以f ′(x)＝1－－＝≤0在[1,2]上恒成立，所以x2－mx－‎4m≤0在[1,2]上恒成立．令g(x)＝x2－mx－‎4m，所以所以m≥，故m的最小值为，选C.‎ ‎[答案] C ‎2．[角度2]已知函数f(x)＝ax2－x＋lnx(a∈R)．‎ ‎(1)求函数f(x)的单调区间；‎ ‎(2)∀m>n>0，>1恒成立，求实数a的取值范围．‎ ‎[解] (1)函数f(x)的定义域为(0，＋∞)，f ′(x)＝2ax－1＋＝.‎ ‎①当a＝0时， f ′(x)＝.‎ 显然，当x∈(0,1)时， f ′(x)>0，函数f(x)单调递增；‎ 当x∈(1，＋∞)时， f ′(x)<0，函数f(x)单调递减．‎ ‎②当a≠0时，对于2ax2－x＋1＝0，Δ＝(－1)2－4×‎2a×1＝1－‎8a.‎ 若Δ≤0，即a≥，因为a>0，所以2ax2－x＋1≥0恒成立，即f ′(x)≥0恒成立，所以函数f(x)在(0，＋∞)上单调递增．‎ 若Δ>0，即00，x2<0.‎ 当x∈时，2ax2－x＋1>0, f ′(x)>0，函数f(x)单调递增；‎ 当x∈时，2ax2－x＋1<0, f ′(x)<0，函数f(x)单调递减．‎ 当0x1>0.‎ 当x∈时，2ax2－x＋1>0, f ′(x)>0，函数f(x)单调递增；‎ 当x∈时，2ax2－x＋1<0, f ′(x)<0，函数f(x)单调递减；‎ 当x∈时，2ax2－x＋1>0, f ′(x)>0，函数f(x)单调递增．‎ 综上，当a＝0时， f(x)的单调递增区间为(0,1)，单调递减区间为(1，＋∞)；‎ 当a≥时，函数f(x)的单调递增区间为(0，＋∞)，无单调递减区间；‎ 当01，即－1>0，也就是>0.‎ 记g(x)＝f(x)－x，则不等式等价于>0，‎ 即函数g(x)＝f(x)－x在(0，＋∞)上单调递增．‎ 由g(x)＝f(x)－x＝ax2－2x＋lnx，可得g′(x)＝2ax－2＋≥0.‎ 因为x>0，所以a≥＝－.‎ 记h(x)＝－(x>0)，则h′(x)＝－－×(－2)×＝.‎ 显然，当x∈(0,1)时，h′(x)>0，函数f(x)单调递增；‎ 当x∈(1，＋∞)时，h′(x)<0，函数f(x)单调递减．‎ 所以h(x)的最大值为h(1)＝－＝，所以a≥.‎ 故实数a的取值范围为.‎ 考点三 利用导数研究函数的极值与最值 ‎1．若在x0附近左侧f ′(x)>0，右侧f ′(x)<0，则f(x0)为函数f(x)的极大值；若在x0附近左侧f ′(x)<0，右侧f ′(x)>0，则f(x0)为函数f(x)的极小值．‎ ‎2．设函数y＝f(x)在[a，b]上连续，在(a，b)内可导，则f(x)在[a，b]上必有最大值和最小值且在极值点或端点处取得．‎ 角度1：根据函数极值的存在情况，利用导数求某些参数的取值范围 A.∪[4，＋∞) B.∪[2，＋∞)‎ C.∪(2，＋∞) D.∪(4，＋∞)‎ ‎ [解析] f ′(x)＝＋x－，由f ′(x)＝0得(x－m)＝0，∴x＝m或x＝.显然m>0.当且仅当00，当x∈(m,2)时，f ′(x)<0，函数f(x)有极大值点x＝m.若0<<2≤m，即m≥2，则当x∈时， f ′(x)>0，当x∈时， f ′(‎ x)<0，函数f(x)有极大值点x＝.综上，m的取值范围是∪[2，＋∞)．故选B.‎ ‎[答案] B 角度2：利用函数的极值与导数的关系，求某些含有参数的较复杂基本函数的极值的大小、个数或最值 ‎[思维流程] (1)→→ ‎(2)→→→‎ ‎[解] (1)由题设知，函数f(x)的定义域为(0，＋∞), f ′(x)＝，且f ′(x)＝0有两个不同的正根，即x2－ax＋a＝0有两个不同的正根，则 ‎∴a>4.‎ ‎(2)不等式f(x1)＋f(x2)<λ(x1＋x2)恒成立等价于λ>恒成立．‎ f(x1)＋f(x2)＝alnx1＋x－ax1＋alnx2＋x－ax2.‎ 由(1)可知x1＋x2＝a，x1x2＝a，‎ ‎∴f(x1)＋f(x2)＝a(lnx1＋lnx2)＋(x＋x)－a(x1＋x2)‎ ‎＝aln(x1x2)＋[(x1＋x2)2－2x1x2]－a(x1＋x2)‎ ‎＝alna＋(a2－‎2a)－a2＝a，‎ ‎∴＝lna－a－1，‎ 令y＝lna－a－1，则y′＝－.‎ ‎∵a>4，∴y′<0，‎ ‎∴y＝lna－a－1在(4，＋∞)上单调递减，‎ ‎∴y2时，f′(x)>0，即f(x)单调递增．‎ ‎∴f(x)只有极小值，且在x＝2时，f(x)取得极小值f(2)＝4－4ln2.‎ ‎(2)∵f′(x)＝，‎ ‎∴当a>0，x∈(0，＋∞)时，f′(x)>0，即f(x)在x∈(0，＋∞)上单调递增，没有最小值；‎ 当a<0时，由f′(x)>0得，x>－，‎ ‎∴f(x)在上单调递增；‎ 由f′(x)<0得，x<－，‎ ‎∴f(x)在上单调递减．‎ ‎∴当a<0时，f(x)的最小值为 f＝aln＋2.‎ 根据题意得f＝aln＋2≥－a，‎ 即a[ln(－a)－ln2]≥0.‎ ‎∵a<0，‎ ‎∴ln(－a)－ln2≤0，解得a≥－2，‎ ‎∴实数a的取值范围是[－2,0)．‎ 热点课题5 导数与函数的单调性与最值 ‎ [感悟体验]‎ ‎ (2017·厦门模拟)已知函数f(x)＝(ax2＋bx＋c)ex在[0,1]上单调递减且满足f(0)＝1，f(1)＝0.‎ ‎(1)求a的取值范围；‎ ‎(2)设g(x)＝f(x)－f′(x)，求g(x)在[0,1]上的最大值和最小值．‎ ‎[解] (1)由f(0)＝1，f(1)＝0，‎ 得c＝1，a＋b＝－1，‎ 则f(x)＝[ax2－(a＋1)x＋1]ex，‎ f′(x)＝[ax2＋(a－1)x－a]ex.‎ 依题意对任意x∈(0,1)，有f′(x)<0.‎ 当a>0时，因为二次函数y＝ax2＋(a－1)x－a的图象开口向上，而f′(0)＝－a<0，‎ 所以有f′(1)＝(a－1)e<0，即00，f(x)不符合条件．‎ 故a的取值范围为0≤a≤1.‎ ‎(2)因g(x)＝(－2ax＋1＋a)ex，‎ g′(x)＝(－2ax＋1－a)ex.‎ ‎(ⅰ)当a＝0时，g′(x)＝ex>0，g(x)在x＝0处取得最小值g(0)＝1，在x＝1处取得最大值g(1)＝e.‎ ‎(ⅱ)当a＝1时，对于任意x∈(0,1)有g′(x)＝－2xex<0，g(x)在x＝0处取得最大值g(0)＝2，‎ 在x＝1处取得最小值g(1)＝0.‎ ‎(ⅲ)当00.‎ ‎①若≥1，即0