吉林省长春市2020届高三二模考试数学（文）试卷 Word版含解析 21页

- 1 - 2020 年吉林省长春市高考数学二模试卷(文科) 一､选择题 1. 已知集合   2 0A x x x   ，  1,0,1,2,3B   ，则 A B  （ ） A.  1,0,3 B.  0,1 C.  0,1,2 D.  0,2,3 【答案】C 【解析】 【分析】 先解一元二次不等式，解出集合 A，然后进行交集的运算即可. 【详解】解：因为  0 2A x x   ，  1,0,1,2,3B   ； ∴  0,1,2A B  . 故选：C. 【点睛】此题考查集合的交集运算，属于基础题. 2. 若 1 (1 )z a i   （ a R ），| 2|z  ，则 a （ ） A. 0 或 2 B. 0 C. 1 或 2 D. 1 【答案】A 【解析】 【分析】 利用复数的模的运算列方程，解方程求得 a 的值. 【详解】由于 1 (1 )z a i   （ a R ），| 2|z  ，所以  221 1 2a   ，解得 0a  或 2a  . 故选：A 【点睛】本小题主要考查复数模的运算，属于基础题. 3. 下列与函数 1y x  定义域和单调性都相同的函数是（ ） A. 2log2 xy  B. 2 1log 2 x y      C. 2 1logy x  D. 1 4y x 【答案】C 【解析】 - 2 - 【分析】 分析函数 1y x  的定义域和单调性，然后对选项逐一分析函数的定义域、单调性，由此确定 正确选项. 【详解】函数 1y x  的定义域为 0,  ，在 0,  上为减函数. A 选项， 2log2 xy  的定义域为 0,  ，在  0,  上为增函数，不符合. B 选项， 2 1log 2 x y      的定义域为 R ，不符合. C 选项， 2 1logy x  的定义域为  0,  ，在 0,  上为减函数，符合. D 选项， 1 4y x 的定义域为 0, ，不符合. 故选：C 【点睛】本小题主要考查函数的定义域和单调性，属于基础题. 4. 已知等差数列 na 中，若 5 73 2a a ，则此数列中一定为 0的是（ ） A. 1a B. 3a C. 8a D. 10a 【答案】A 【解析】 【分析】 将已知条件转化为 1,a d 的形式，由此确定数列为 0 的项. 【详解】由于等差数列 na 中 5 73 2a a ，所以    1 13 4 2 6a d a d   ，化简得 1 0a  ，所 以 1a 为 0 . 故选：A 【点睛】本小题主要考查等差数列的基本量计算，属于基础题. 5. 若单位向量 1e  、 2e  夹角为 60 ， 1 22a e e    ，则 a  （ ） A. 4 B. 2 C. 3 D. 1 【答案】C - 3 - 【解析】 【分析】 利用平面数量积的定义和运算性质计算出 2 a  的值，进而可得出 a r 的值. 【详解】由于位向量 1e  、 2e  夹角为 60 ，则 1 2 1 2 1cos60 2e e e e       ，  22 2 2 1 2 1 1 2 2 12 4 4 4 4 1 32a e e e e e e                  ，因此， 3a  . 故选：C. 【点睛】本题考查利用平面向量数量积计算平面向量的模，考查计算能力，属于基础题. 6. 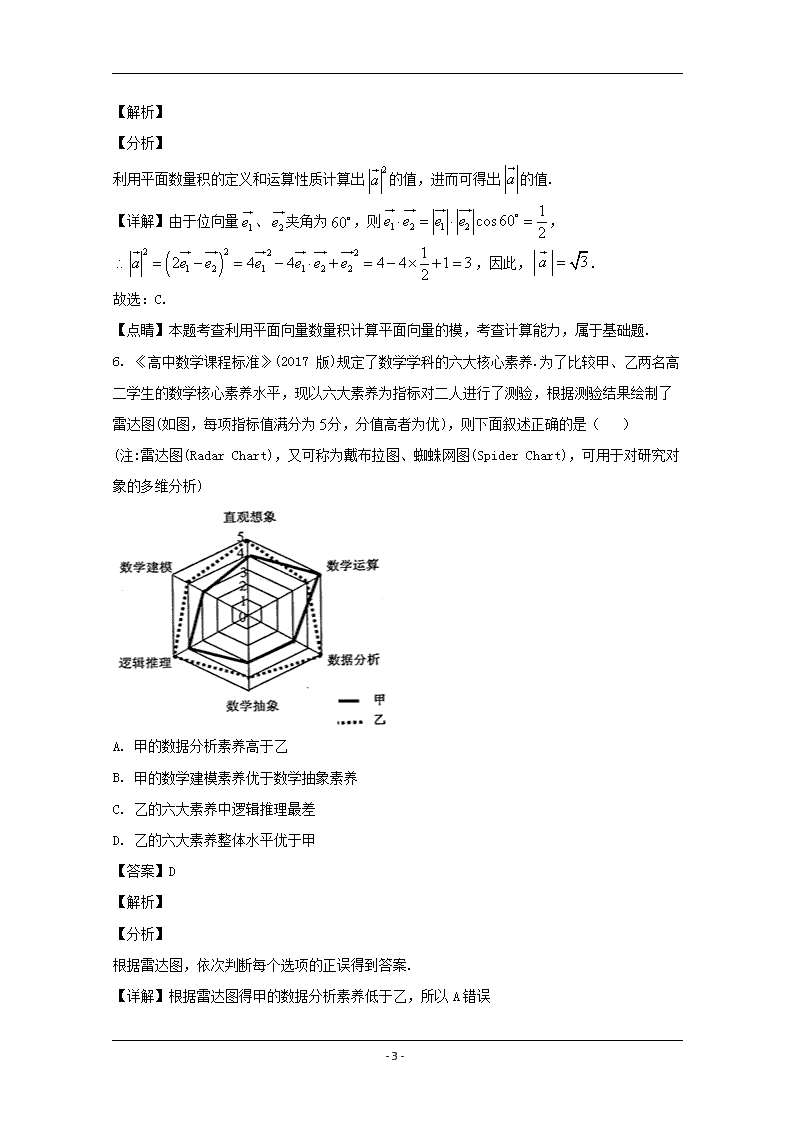《高中数学课程标准》(2017 版)规定了数学学科的六大核心素养.为了比较甲、乙两名高 二学生的数学核心素养水平，现以六大素养为指标对二人进行了测验，根据测验结果绘制了 雷达图(如图，每项指标值满分为 5 分，分值高者为优)，则下面叙述正确的是（ ） (注:雷达图(Radar Chart)，又可称为戴布拉图、蜘蛛网图(Spider Chart)，可用于对研究对 象的多维分析) A. 甲的数据分析素养高于乙 B. 甲的数学建模素养优于数学抽象素养 C. 乙的六大素养中逻辑推理最差 D. 乙的六大素养整体水平优于甲 【答案】D 【解析】 【分析】 根据雷达图，依次判断每个选项的正误得到答案. 【详解】根据雷达图得甲的数据分析素养低于乙，所以 A 错误 - 4 - 根据雷达图得甲的数学建模素养等于数学抽象素养，所以 B 错误 根据雷达图得乙的六大素养中数学建模和数学抽象最差，所以 C 错误 根据雷达图得乙整体为 27 分，甲整体为 22 分，乙的六大素养整体水平优于甲，所以 D 正确 故答案选 D 【点睛】本题考查了雷达图，意在考查学生解决问题的能力. 7. 命题 p ：存在实数 0x ，对任意实数 x ，使得  0sin sinx x x   恒成立； q： 0a  ， ( ) ln a xf x a x   为奇函数，则下列命题是真命题的是（ ） A. p q B. ( ) ( )p q   C. ( )p q  D. ( )p q  【答案】A 【解析】 【分析】 分别判断命题 p 和 q的真假性，然后根据含有逻辑联结词命题的真假性判断出正确选项. 【详解】对于命题 p ，由于  sin sinx x   ，所以命题 p 为真命题.对于命题 q，由于 0a  ， 由 0a x a x   解 得 a x a   ， 且     1 ln ln lna x a x a xf x f xa x a x a x               ，所以  f x 是奇函数，故 q为真命题. 所以 p q 为真命题. ( ) ( )p q   、 ( )p q  、 ( )p q  都是假命题. 故选：A 【点睛】本小题主要考查诱导公式，考查函数的奇偶性，考查含有逻辑联结词命题真假性的 判断，属于基础题. 8. 已知函数 ln , 0( ) 2 ( 2), 0 x xf x x x x      ，则函数 ( ) 3y f x  的零点个数是（ ） A. 1 B. 2 C. 3 D. 4 【答案】B 【解析】 【分析】 对 x 分 0, 0x x  两种情况求方程 ( ) 3=0f x  的根的个数即得解. - 5 - 【详解】当 0x  时， 3| ln | 3 0, ln 3,x x x e       或 3e ，都满足 0x  ； 当 0x  时， 2 22 4 3 0, 2 4 3 0, 2 0, 16 4 2 3 0x x x x               ， 所以方程没有实数根. 综合得函数 ( ) 3y f x  的零点个数是 2. 故选：B 【点睛】本题主要考查函数的零点的个数的求法，意在考查学生对该知识的理解掌握水平和 分析推理能力. 9. 已知 为锐角，且 sin 3 tan 3sin 3                 ，则角  （ ） A. 12  B. 6  C. 4  D. 3  【答案】C 【解析】 【分析】 对 sin 3 tan 3sin 3                 先化切为弦，再利用和角差角的正余弦公式化简即得解. 【详解】由题得 sin sin3 3 , cos( )sin 33                       为锐角，∴sin cos( )3 3         ∴ 1 3 1 3sin cos cos sin , sin cos , tan 12 2 2 2              . 因为 为锐角，∴ = 4  . 故选：C 【点睛】本题主要考查同角的三角函数关系和和角差角的正余弦公式的应用，意在考查学生 对这些知识的理解掌握水平. - 6 - 10. 若双曲线 2 2 2 2 1x y a b   （ 0a  ， 0b  ）的一条渐近线被圆 2 2 4 0x y y   截得的弦长 为 2，则双曲线的离心率为（ ） A. 2 B. 3 C. 2 2 3 D. 2 3 3 【答案】D 【解析】 【分析】 求得双曲线的一条渐近线方程，求得圆心和半径，运用点到直线的距离公式和弦长公式，可 得 a ，b 的关系，即可得到所求的离心率． 【详解】双曲线 2 2 2 2: 1( 0, 0)x yC a ba b     的一条渐近线方程设为 0bx ay  ， 由题得圆 2 2( 2) 4x y   的圆心为 (0,2) ，半径 2r = ， 可得圆心到渐近线的距离为 2 2 | 0 2 |ad b a   ， 则 2 2 2 42 2 4 a b a    ，化为 2 23a b= ，所以 2 2 1 ,3 b a  2 2 1 2 31 1 3 3 c be a a       ， 故选： D ． 【点睛】本题主要考查双曲线的方程和性质，考查直线和圆的位置关系，考查方程思想和运 算能力，属于基础题． 11. 已知数列 na 的前 n 项和为 nS ，且 1 2a  ， 1 2 n n na Sn  （ *nN ），则 nS  （ ） A. 12 1n  B. 2nn C. 3 1n  D. 12 3nn  【答案】B 【解析】 【分析】 由题得 1 22 ,1 n n a n a n     再利用累乘法求出 1( 1) 2n na n    ，即得 nS . - 7 - 【详解】由题得 1 1 1 ( 1) ( 1), , ,2 1 2 1 n n n n n n n na n a na n aS S an n n n              （ 2n  ） 所以 1 22 ,1 n n a n a n     （ 2n  ） 由题得 2 2 1 66, 32 aa a     ，所以 1 22 ,1 n n a n a n     （ 1n  ）. 所以 32 4 1 2 3 1 3 4 5 12 , 2 , 2 , 2 ,2 3 4 n n a aa a n a a a a n        ， 所以 1 1 1 12 , ( 1) 22 n nn n a n a na        . 所以 ( 2) 2 22 n n n nS n nn       . 故选：B 【点睛】本题主要考查数列通项的求法，考查数列前 n 项和与 na 的关系，意在考查学生对这 些知识的理解掌握水平. 12. 在正方体 1 1 1 1ABCD A B C D 中，点 E ， F ，G 分别为棱 1 1A D ， 1D D ， 1 1A B 的中点， 给出下列命题：① 1AC EG ；② //GC ED ；③ 1B F  平面 1BGC ；④ EF 和 1BB 成角为 4  . 正确命题的个数是（ ） A. 0 B. 1 C. 2 D. 3 【答案】C 【解析】 【分析】 建立空间直角坐标系，利用向量的方法对四个命题逐一分析，由此得出正确命题的个数. 【 详 解 】 设 正 方 体 边 长 为 2 ， 建 立 空 间 直 角 坐 标 系 如 下 图 所 示 ，      12,0,0 , 0,2,2 , 2,1,2A C G ，            10,2,0 , 1,0,2 , 0,0,0 , 2,2,2 , 0,0,1 , 2,2,0C E D B F B . ①，    1 12,2,2 , 1,1,0 , 2 2 0 0AC EG AC EG            ，所以 1AC EG ，故①正确. ②，    2,1, 2 , 1,0, 2GC ED       ，不存在实数  使G C ED  ，故 //GC ED 不成立， - 8 - 故②错误. ③，      1 12, 2, 1 , 0, 1,2 , 2,0,2B F BG BC          ， 1 1 10, 2 0B F BG B F BC        ， 故 1B F  平面 1BGC 不成立，故③错误. ④，    11,0, 1 , 0,0,2EF BB     ，设 EF 和 1BB 成角为 ，则 1 1 2 2cos 22 2 EF BB EF BB           ，由于 0, 2      ，所以 4   ，故④正确. 综上所述，正确的命题有 2 个. 故选：C 【点睛】本小题主要考查空间线线、线面位置关系的向量判断方法，考查运算求解能力，属 于中档题. 二､填空题 13. 若 ,x y 满足约束条件 2 2 2 0 2 2 x y y x y         ，则 z x y  的最大值为__________． 【答案】4 【解析】 【详解】作出可行域如图所示： - 9 - 由 2 2 2 x y y     ，解得  2,2A . 目标函数 z x y  ，即为  y x z   ，平移斜率为-1 的直线，经过点  2,2A 时， 2 2 4maxz    . 14. 曲线 ( ) 2sinf x x 在 3x  处的切线与直线 1 0ax y   垂直，则 a ________. 【答案】1 【解析】 【分析】 先求出切线的斜率 ( ) 1,3k f   解方程1 ( ) 1a    即得解. 【详解】由题得 ( ) 2cos , ( ) 1.3f x x k f      所以1 ( ) 1, 1a a      . 故答案为：1 【点睛】本题主要考查导数的几何意义，考查两直线垂直的性质，意在考查学生对这些知识 的理解掌握水平. 15. 在半径为 2 的圆上有 A ， B 两点，且 2AB  ，在该圆上任取一点 P ，则使得 PAB 为 锐角三角形的概率为________. 【答案】 1 6 【解析】 【分析】 如图，当点 P 在劣弧 CD 上运动时， PAB 为锐角三角形.求出劣弧 CD 的长，再利用几何概型 - 10 - 的概率公式求解. 【详解】 如图，四边形 ABCD 是矩形，当点 P 在劣弧 CD 上运动时， PAB 为锐角三角形. 由于 OD=OC=CD=2，所以 3COD   , 所以劣弧 CD 的长为 22 =3 3   ， 由几何概型的概率公式得 2 13 =2 2 6P    . 故答案为： 1 6 【点睛】本题主要考查几何概型的概率的计算，意在考查学生对这些知识的理解掌握水平. 16. 三棱锥 A BCD 的顶点都在同一个球面上，满足 BD 过球心O ，且 2 2BD  ，则三棱 锥 A BCD 体积的最大值为________；三棱锥 A BCD 体积最大时，平面 ABC 截球所得的 截面圆的面积为________. 【答案】 (1). 2 2 3 (2). 4 3  【解析】 【分析】 由于 BD 是球的直径，故当 ,OC BD OA BD  时，三棱锥 A BCD 体积取得最大值，由此 求得体积的最大值.求得三棱锥 A BCD 体积最大时，等边三角形 ABC 的外接圆半径，由此 求得等边三角形 ABC 的外接圆的面积，也即求得平面 ABC 截球所得的截面圆的面积. 【详解】依题意可知，BD 是球的直径，所以当 ,OC BD OA BD  ，即 2OC OA  时， - 11 - 三棱锥 A BCD 体积取得最大值为 1 1 1 2 22 2 2 23 3 2 3BCDS OA        .此时 2BC AC AB   ，即三角形 ABC 是等边三角形，设其外接圆半径为 r ，由正弦定理得 2 12 3sin 3 r r    ，所以等边三角形 ABC 的外接圆的面积，也即平面 ABC 截球所得的 截面圆的面积为 2 2 1 44 4 33 r         . 故答案为：(1). 2 2 3 (2). 4 3  【点睛】本小题主要考查几何体外接球的有关计算，考查球的截面面积的计算，考查空间想 象能力，属于中档题. 三､解答题 17. 已知在 ABC 的三个内角分别为 A 、 B 、C ， 2sin sin 2 cosB A A ， 1cos 3B  . （1）求 A 的大小； （2）若 2AC  ，求 AB 长. 【答案】（1） 3A  （2） 6 14  【解析】 【分析】 （ 1 ） 由 题 得 2 2sin 3B  ， 再 解 方 程  22 1 cos 3cosA A  即 得 解 ；（ 2 ） 求 出 - 12 - 3 2 2sin 6C  ，再利用正弦定理得解. 【详解】（1）由题得 2 2sin 3B  ， 所以 22sin 3cosA A ，所以  22 1 cos 3cosA A  ， 解得 1cos 2A  ， (0, )A  ，∴ 3A  . （2）sin sin( ) sin cos cos sinC A B A B A B    3 1 1 2 2 3 2 2 2 3 2 3 6      由正弦定理 sin sin AB AC C B  得 6sin 1sin 4 ACAB CB     . 【点睛】本题主要考查同角的三角函数关系，考查和角的正弦公式的应用，考查正弦定理解 三角形，意在考查学生对这些知识的理解掌握水平. 18. 2019 年入冬时节，长春市民为了迎接 2022 年北京冬奥会，增强身体素质，积极开展冰上 体育锻炼.现从速滑项目中随机选出 100 名参与者，并由专业的评估机构对他们的锻炼成果进 行评估打分（满分为 100 分）并且认为评分不低于 80 分的参与者擅长冰上运动，得到如图所 示的频率分布直方图： （1）求 m 的值； （2）将选取的 100 名参与者的性别与是否擅长冰上运动进行统计，请将下列 2 2 列联表补充 完整，并判断能否在犯错误的概率在不超过 0.01 的前提下认为擅长冰上运动与性别有关系？ 擅长 不擅长 合计 - 13 - 男性 30 女性 50 合计 100  2P K k 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 （ 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d      ，其中 n a b c d    ） 【答案】（1） 0.025m  （2）填表见解析；不能在犯错误的概率不超过 0.01 的前提下认为擅 长冰上运动与性别有关系 【解析】 【分析】 （1）利用频率分布直方图小长方形的面积和为1列方程，解方程求得 m 的值. （2）根据表格数据填写 2 2 列联表，计算出 2K 的值，由此判断不能在犯错误的概率不超过 0.01 的前提下认为擅长冰上运动与性别有关系. 【详解】（1）由题意 0.005 2 0.015 0.02 0.03 10 1m       ，解得 0.025m  . （2）由频率分布直方图可得不擅长冰上运动的人数为 0.025+0.003 10 100 30   . 完善列联表如下： 擅长 不擅长 合计 男性 20 30 50 女性 10 40 50 合计 30 70 100 - 14 - 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d      2100 (800 300) 4.76250 50 30 70      ， 对照表格可知， 4.762 6.635 ， 不能在犯错误的概率不超过 0.01 的前提下认为擅长冰上运动与性别有关系. 【点睛】本小题主要考查根据频率分布直方图计算小长方形的高，考查 2 2 列联表独立性检 验，属于基础题. 19. 如图，直三棱柱 1 1 1ABC A B C 中，底面 ABC 为等腰直角三角形， AB BC ， 1 2 4AA AB  ， M ， N 分别为 1CC ， 1BB 的中点，G 为棱 1AA 上一点，且 1A B NG . （1）求证 1A B GM ； （2）求点 1A 到平面 MNG 的距离. 【答案】（1）证明见解析（2） 6 5 5 【解析】 【分析】 （1）先证明 1A B  平面 MNG, 1A B  MG 即得证；（2）设 1A B 与 GN 交于点 E ，先求出 4 5 5BE  ，再求出 1 6 5 5A E  即得解. 【详解】（1）由题意平面 1 1ABB A  平面 1 1BCC B ，因为 1MN BB , 所以 MN  平面 1 1ABB A ,因为 1A B  平面 1 1ABB A , 所以 1MN A B ,因为 1GN A B , ,MN GN  平面 MNG , MN GN N , - 15 - 所以 1A B  平面 MNG, 因为 MG  平面 MNG, 所以 1A B  MG. （2）设 1A B 与GN 交于点 E ， 在直角△ 1 1A BB 中， 1 1 4 2cos 552 5 A BB   , 在直角 BNE 中， 1 1 2cos 55 2 BE BEA BB BN     ,所以 4 5 5BE  ， 则 1 4 5 6 52 5 5 5A E    ， 因为 1A B  平面 MNG,所以 1A E 就是 1A 到平面 MNG 的距离， 可知 1A 到平面 MNG 的距离为 6 5 5 . 【点睛】本题主要考查直线平面位置关系的证明，考查空间点到平面距离的计算，意在考查 学生对这些知识的理解掌握水平. 20. 已知椭圆C ： 2 2 2 2 1x y a b   （ 0a b  ）的左、右顶点分别为 A 、 B ，焦距为 2，点 P 为 椭圆上异于 A 、 B 的点，且直线 PA 和 PB 的斜率之积为 3 4  . （1）求C 的方程； （2）设直线 AP 与 y 轴的交点为Q ，过坐标原点 O 作 //OM AP 交椭圆于点 M ，试证明 2 | | | | | | AP AQ OM  为定值，并求出该定值. - 16 - 【答案】（1） 2 2 14 3 x y  （2）证明见解析；该定值为 2 【解析】 【分析】 （1）由已知得 2 2 3 4 b a  ，且 1c  ，即得椭圆的标准方程；（2）设直线 AP 的方程为： ( 2)y k x  ， 求出 2 2 6 8 3 4p kx k   ， 2 2 12 3 4Mx k   ，再计算 2 | | | | | | AP AQ OM  得其值为定值. 【详解】（1）已知点 P 在椭圆C ： 2 2 2 2 1x y a b   （ 0a b  ）上， 可设  0 0,P x y ，即 2 2 0 0 2 2 1x y a b   ， 又 2 2 0 0 0 2 2 2 0 0 0 3 4AP BP y y y bk k x a x a x a a           ， 且 2 2c  ，可得椭圆C 的方程为 2 2 14 3 x y  . （2）设直线 AP 的方程为： ( 2)y k x  ，则直线 OM 的方程为 y kx . 联立直线 AP 与椭圆C 的方程可得：  2 2 2 23 4 16 16 12 0k x k x k     ， 由 2Ax   ，可得 2 2 6 8 3 4p kx k   ， 联立直线 OM 与椭圆C 的方程可得： 2 23 4 12 0k x   ， 即 2 2 12 3 4Mx k   ，即 2 22 2 | 0 2 || | | | 2| | p A Q P M M Ax x x x xAP AQ OM x x          . 【点睛】本题主要考查椭圆标准方程的求法，考查椭圆中的定值问题，意在考查学生对这些 知识的理解掌握水平. 21. 已知函数 3 21( ) 3f x x x mx m    . （1）若 1x 为 ( )f x 的极值点，且    1 2f x f x （ 1 2x x ），求 1 22x x 的值. （2）求证：当 0m  时， ( )f x 有唯一的零点. - 17 - 【答案】（1） 1 22 3x x   （2）证明见解析 【解析】 【分析】 （1）由题得 2 2 1 1 2 2 1 2+ + +3 +3 +3 0x x x x x x m  ， 2 1 13 6 3 0x x m   ，对两式消元因式分解即 得 1 22x x 的值；（2）由题得 3 21 ( 1)3 x x m x    ，再分析 3 21( ) 3h x x x  和 ( 1)y m x   的图象即得当 0m  时， ( )f x 有唯一的零点. 【详解】（1）由题得 2( ) 2f x x x m    ， 由题可知    1 2f x f x ，所以 3 2 3 2 1 1 1 2 2 2 1 1 3 3x x mx m x x mx m       ， 所以 2 2 1 1 2 2 1 2+ + +3 +3 +3 0x x x x x x m  （i） 因为  1 0 f x ，所以 2 1 12 0x x m   .即 2 1 13 6 3 0x x m   （ii） （ii）-（i）得 2 2 1 1 2 2 1 2 1 2 1 2 1 22 3 3 0, (2 )( ) 3( ) 0x x x x x x x x x x x x           ， 所以 1 2 1 2 1 2 1 2(2 3)( ) 0, , 2 3x x x x x x x x         . （2）令 3 21( ) 03f x x x mx m     ，则 3 21 ( 1)3 x x m x    ， 令 3 21( ) 3h x x x  ， 2( ) 2h x x x   ， 可知 ( )h x 在 ( , 2)  和 (0, ) 上单调递增，在 2,0 上单调递减， 又 4( 2) 3h   ， (0) 0h  ； ( 1)y m x   为过 ( 1,0) 点的直线，又 0m  ，则 0m  ， 因此 3 21 ( 1)3 x x m x    有且只有一个交点， 即 3 21( ) 3f x x x mx m    有唯一的零点. 【点睛】本题主要考查利用导数研究函数的零点和极值，意在考查学生对这些知识的理解掌 握水平. 22. 已知曲线 1C 的参数方程为 2 2cos 2sin x y       （ 为参数），曲线 2C 的参数方程为 - 18 - 38 cos 4 3sin 4 x t y t        （t 为参数）. （1）求 1C 和 2C 的普通方程； （2）过坐标原点 O 作直线交曲线 1C 于点 M （ M 异于O ），交曲线 2C 于点 N ，求 | | | | ON OM 的 最小值. 【答案】（1）曲线 1C 的普通方程为： 2 2( 2) 4x y   ；曲线 2C 的普通方程为： 8 0x y   （2） 4( 2 1) 【解析】 【分析】 （1）消去曲线 1 2,C C 参数方程中的参数，求得 1C 和 2C 的普通方程. （2）设出过原点O 的直线的极坐标方程，代入曲线 1 2,C C 的极坐标方程，求得 ,ON OM 的 表达式，结合三角函数值域的求法，求得 | | | | ON OM 的最小值. 【详解】（1）曲线 1C 的普通方程为： 2 2( 2) 4x y   ； 曲线 2C 的普通方程为： 8 0x y   . （2）设过原点的直线的极坐标方程为 30 , ,4 R             ； 由 2 2( 2) 4x y   得 2 2 4 0x y x   ，所以曲线 1C 的极坐标方程为 4cos  在曲线 1C 中， 4| o| c sOM  . 由 8 0x y   得曲线 2C 的极坐标方程为 cos sin 8 0      ，所以 而O 到直线与曲线 2C 的交点 N 的距离为 8| | sin cosON    ， 因此 2 8 | | 2 4sin cos | | 4cos sin cos cos 2 sin 2 14 ON OM                ， - 19 - 即 | | | | ON OM 的最小值为 4 4( 2 1) 2 1    . 【点睛】本小题主要考查参数方程化为普通方程，考查直角坐标方程化为极坐标方程，考查 极坐标系下距离的有关计算，属于中档题. 23. 已知函数 ( ) | 1| | 1|f x ax x    . （1）若 2a  ，解关于 x 的不等式 ( ) 9f x  ； （2）若当 0x  时， ( ) 1f x  恒成立，求实数 a 的取值范围. 【答案】（1） | 3 3x x   （2）  0,a   【解析】 【分析】 （1）利用零点分段法将  f x 表示为分段函数的形式，由此求得不等式的解集. （2）对 a 分成 0, 0, 0a a a   三种情况，求得  f x 的最小值，由此求得 a 的取值范围. 【详解】（1）当 2a  时， 3 , 1 1( ) 2 1 1 2, 12 13 , 2 x x f x x x x x x x                 ， 由此可知， ( ) 9f x  的解集为 | 3 3x x   （2）当 0a  时，       1 , 1 1( ) 1 1 1 2, 1 11 , a x x f x ax x a x xa a x x a                    ( )f x 的最小值为 1f a     和  1f 中的最小值，其中 1 11 1f a a        ， (1) 1 1f a   . 所以 ( ) 1f x  恒成立. 当 0a  时， ( ) 1 1 1f x x    ，且 (1) 1f  ， ( ) 1f x  不恒成立，不符合题意. - 20 - 当 0a  时，   1 11 1 , 1f a f a a         ， 若 2 0a   ，则  1 1f  ，故 ( ) 1f x  不恒成立，不符合题意； 若 2a   ，则 1 1f a      ，故 ( ) 1f x  不恒成立，不符合题意. 综上，  0,a   . 【点睛】本小题主要考查绝对值不等式的解法，考查根据绝对值不等式恒成立求参数的取值 范围，考查分类讨论的数学思想方法，属于中档题. - 21 -