【数学】2018届一轮复习北师大版三角函数的诱导公式学案 6页

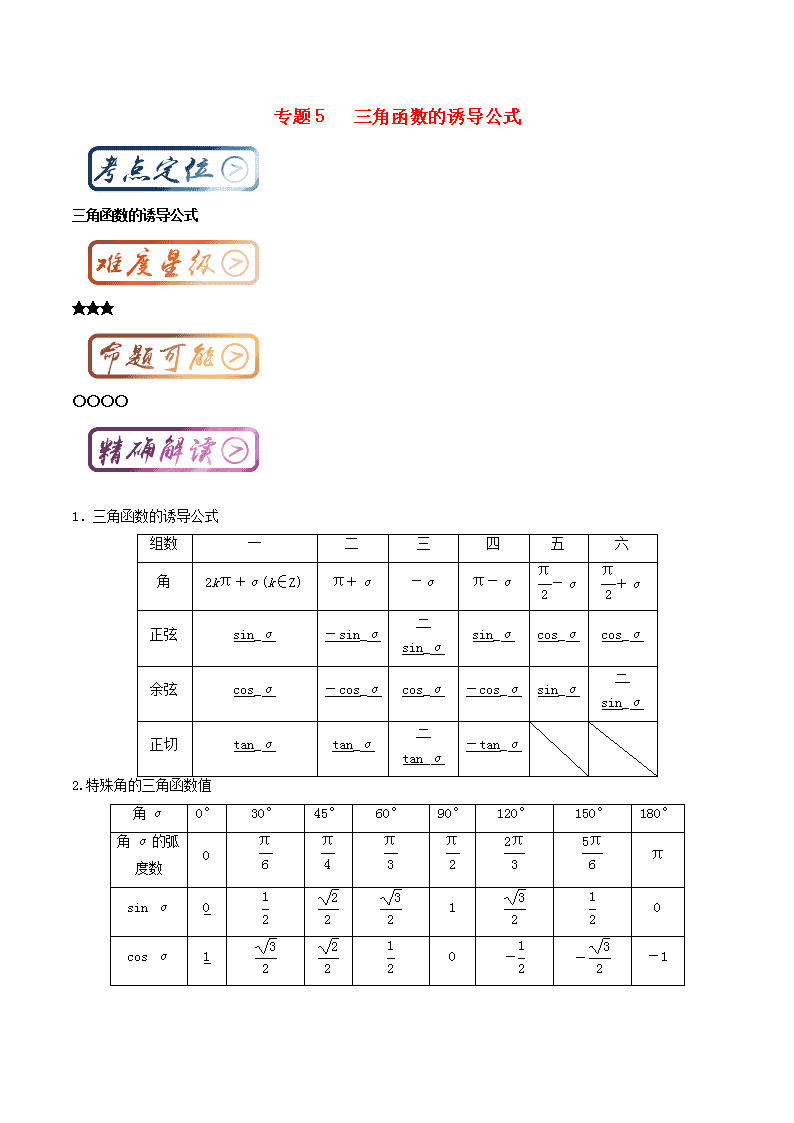
专题5 三角函数的诱导公式 三角函数的诱导公式 ‎★★★‎ ‎○○○○‎ ‎1．三角函数的诱导公式 组数 一 二 三 四 五 六 角 ‎2kπ＋α(k∈Z)‎ π＋α ‎－α π－α －α ＋α 正弦 sin_α ‎－sin_α ‎－sin_α sin_α cos_α cos_α 余弦 cos_α ‎－cos_α cos_α ‎－cos_α sin_α ‎－sin_α 正切 tan_α tan_α ‎－tan_α ‎－tan_α ‎2.特殊角的三角函数值 角α ‎0°‎ ‎30°‎ ‎45°‎ ‎60°‎ ‎90°‎ ‎120°‎ ‎150°‎ ‎180°‎ 角α的弧度数 ‎0‎ π sin α ‎0‎ ‎1‎ ‎0‎ cos α ‎1‎ ‎0‎ ‎－ ‎－ ‎－1‎ tan α ‎0‎ ‎1‎ ‎－ ‎－ ‎0‎ ‎1.利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤 也就是：“负化正，大化小，化到锐角就好了”．‎ ‎2．利用诱导公式化简三角函数的要求 ‎(1)化简过程是恒等变形；‎ ‎(2)结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值．‎ ‎[典例]　(1)若sin α是方程5x2－7x－6＝0的根，则＝(　　)‎ A. B. C. D. ‎(2)求值：sin(－1 200°)cos 1 290°＋cos(－1 020°)·sin(－1 050°)＝________.‎ ‎[解析]　(1)方程5x2－7x－6＝0的两根为x1＝－，x2＝2，则sin α＝－.‎ 原式＝＝－＝.‎ ‎(2)原式＝－sin 1 200°cos 1 290°－cos 1 020°sin 1 050°‎ ‎＝－sin(3×360°＋120°)cos(3×360°＋210°)－cos(2×360°＋300°)sin(2×360°＋330°)‎ ‎＝－sin 120°cos 210°－cos 300°sin 330°‎ ‎＝－sin (180°－60°)cos(180°＋30°)－cos(360°－60°)·sin(360°－30°)‎ ‎＝sin 60°cos 30°＋cos 60°sin 30°‎ ‎＝×＋×＝1.‎ ‎[答案]　(1)B　(2)1‎ ‎1．若 A. B. C. D. ‎ ‎2．已知是锐角，且，则__________．‎ ‎【来源】【全国市级联考】山东省菏泽市2018届高三上学期期中考试数学（文）试题（B）‎ ‎【答案】‎ ‎【解析】，‎ 故答案为： ‎ ‎3．已知角的张终边经过点， 且为第二象限．‎ ‎（1）求的值；‎ ‎（2）若，求的值．‎ ‎【来源】【全国区级联考】江苏省沛县、如皋市2017-2018学年高一上学期教学质量调研二（期中）数学试题 ‎【答案】（1）；（2）.‎ 试题解析：‎ ‎（1）由三角函数定义可知，‎ 解得 为第二象限角，‎ ‎ .‎ ‎（2）由知,‎ ‎1．已知sin＝，那么cos α＝(　　)‎ A．－ B．－ C. D. 解析：选C　∵sin＝sin＝cos α，∴cos α＝.‎ ‎2．sin 210°cos 120°的值为(　　)‎ A. B．－ C．－ D. 解析：选A　sin 210°cos 120°＝－sin 30°(－cos 60°)＝－×＝.‎ ‎3．已知A＝＋(k∈Z)，则A的值构成的集合是(　　)‎ A．{1，－1,2，－2} B．{－1,1} ‎ C．{2，－2} D．{1，－1,0,2，－2}‎ 解析：选C　k为偶数时，A＝＋＝2；k为奇数时，A＝＋＝－2.则A的值构成的集合为{2，－2}．‎ ‎4．已知tan＝，则tan＝________.‎ ‎5．已知α为第三象限角，‎ f(α)＝.‎ ‎(1)化简f(α)；‎ ‎(2)若cos＝，求f(α)的值．‎ 解：(1)f(α)＝ ‎＝＝－cos α.‎ ‎(2)∵cos＝，‎ ‎∴－sin α＝，从而sin α＝－.‎ 又α为第三象限角，‎ ‎∴cos α＝－＝－，‎ ‎∴f(α)＝－cos α＝. ‎ ‎________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________‎