【数学】2020届一轮复习北师大版集合与常用逻辑用语学案 6页

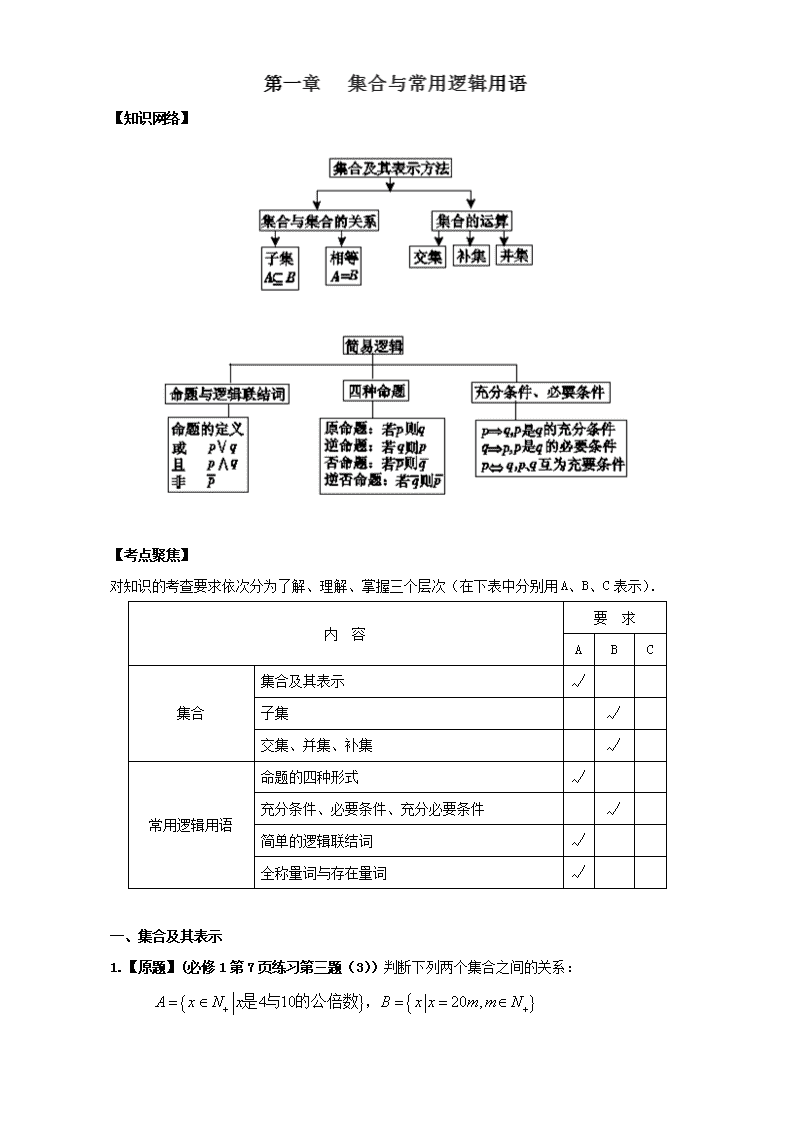
【知识网络】 【考点聚焦】 对知识的考查要求依次分为了解、理解、掌握三个层次（在下表中分别用 A、B、C 表示）． 要 求 内 容 A B C 集合及其表示 √ 子集 √集合 交集、并集、补集 √ 命题的四种形式 √ 充分条件、必要条件、充分必要条件 √ 简单的逻辑联结词 √ 常用逻辑用语 全称量词与存在量词 √ 一、集合及其表示 1.【原题】(必修 1 第 7 页练习第三题（3））判断下列两个集合之间的关系： { } { }4 10 20 ,A x N x B x x m m N+ += ∈ = = ∈是 与 的公倍数 ， 【原题解读】 （1）知识上；需要熟悉集合的表达方式，明确集合间关系（子集，真子集，相等）的概念。 （2）思路方法上；需要能对无限集合的关系进行判断，可采用列举法或数学表达的转换和 统一来确定集合间的关系。体现的数学思想有对应思想及数学符号表达能力。 变式【2018 新课标高考】已知集合 ，集合 ，则 （ ） A． B． C． D． 【答案】D. 【解析】由题可得； ， ，故选 D. 二、集合的运算 1.【原题】（必修 1 第十二页习题 1.1B 组第 1 题）已知集合 A={1，2}，集合 B 满足 A∪B={1， 2}，则这样的集合 B 有个. 【解析】∵A={1，2}，又 A∪B={1，2}，∵ ，则 B 集合可以是： ，{1}，{2}，{1，2}； 有 4 个； 【原题解读】本题需要注意 ，则问题可化为求集合 A 的子集个数问题， 即为 。 变式 1【2018 北京模拟】已知 ，若非空集合 A 满足，对任意 都有 ，则这样的集合 有个。 【答案】7 【解析】符合条件的集合 A 有 ，共 7 个 变式 2 已知集合 有个元素，则集合 的子集个数有 个，真子集个数有 个. 4 x xM x N N∗ ∗ = ∈ ∈  且 10 40 xN x Z = ∈   M N= N M⊆ 20 xM N x Z = ∈   40 xM N x N ∗ = ∈   { }20 ,M x x k k N ∗= = ∈ { }40 ,N x x k k Z= = ∈ B A⊆ ∅ A B A B A∪ = ⇔ ⊆ 22 { }1,2,3,4,5U = ,a A∈ 6 a A− ∈ A { } { } { } { } { } { } { }1,5 , 2,4 , 3 , 1,3,5 , 2,3,4 , 1,2,4,5 , 1,2,3,4,5 A A 【答案】 ； . 变式 3 满足条件 的所有集合 的个数是 个. 【答案】4. 【解析】3 必须在集合 里面， 的个数相当于 2 元素集合的子集个数，故有 4 个. 2.【原题】（必修 1 第四十四页复习参考题 A 组第 4 题）已知集合 ，集合 ，若 ，求实数的值. 【原题解读】本题给出集合为两个方程的根，而条件 ，可对集合 B 的情况进行分类，从 而求出的值；体现了分类思想和对集合语言的深刻理解和运用。 注意；空集是一个特殊的集合，它不含任何元素，是任何集合的子集，是任何非空集合的真子 集，在解决集合之间关系问题时，它往往易被忽视而引起解题失误。 变式【2018 邯郸模拟】已知集合 ，集合 B= 若 ,求实数 p 的取值范围。 【答案】 【解析】由（1)B= 时，即 p+12p-1,故 p2; （2）B 时， ，又 ， 则；借助数轴表示知 ， 故 。由（1）（2）得 。 3. 原 题 ( 必 修 1 第 十 二 页 习 题 1.1 A 组 第 10 题 ） 已 知 集 合 ， ，求 ， ， ， 变式 1 已知全集 且 则 等于 （ ） A. B. C. D. 【答案】C. 【解析】集合 ，所以 ，集合 2n 2 1n − { } { }1,2 1,2,3A = A A A { }2 1A x x= = { }1B x ax= = AB ⊆ AB ⊆ { }52| ≤≤−= xxA { }121| −≤≤+= pxpxA A B B= 3≤p ∅ ∅≠ 2p ≥ AB ⊆ 1 2 2 1 5p p+ ≥ − − ≤且 32 ≤≤ p 3≤p { }| 3 7A x x= ≤ < { }| 2 10B x x= < < ( )RC A B ( )RC A B ( )RC A B ( )RA C B ,U R= { } { }2| 1 2 , | 6 8 0 ,A x x B x x x= − > = − + < ( )UC A B [ 1,4)− (2,3) (2,3] ( 1,4)− { } { }|| 1| 2 | 3 1A x x x x x= − > = > < −或 { }| 1 3UC A x x= − ≤ ≤ ，所以 为 ，故选 C . 变式 2 设集合 ， ，则 等于 （ ） A． B． C． D． 【答案】B. 【解析】 ， ，所以 ，故选 B . 变 式 3 已知集合 集合 则 等于 （ ） A． B． C． D． 【答案】D. 【解析】集合 ，故选 D . 【感受高考】 1. 【2018 新课标 1 理】设集合 ， ，则 （ ） （A） （B） （C） （D） 【答案】D 【解析】 2.【2018 高考新课标 2 理数】已知集合 ， ，则 （ ） （A） （B） （C） （D） 【答案】C 【解析】 试题分析：集合 ，而 ， {1, }A = 2, 3 { | ( 1)( 2) 0, }B x x x x= + − < ∈Z A B = {1} {1 2}， {01 2 3}，，， { 1 01 2 3}− ，，，， B {x | 1 x 2,x Z} {0,1}= − < < ∈ = A {1,2,3}= { } { }2| 6 8 0 | 2 4B x x x x x= − + < = < < ( )UC A B (2,3] { }2 2,A x x x R= − ≤ ∈ { }2| , 1 2B y y x x= = − − ≤ ≤ ( )RC A B R { }, 0x x R x∈ ≠ { }0 ∅ [0,4]A = [ 4,0]B = − ( ) {0}R RC A B C= { }|1 10 ,P x N x= ∈ ≤ ≤ { }2| 6 0 ,Q x R x x= ∈ + − = P Q { }1,2,3 { }2,3 { }1,2 { }2 { } { }2| 6 0 3,2Q x R x x= ∈ + − = = − 2{ | 4 3 0}A x x x= − + < { | 2 3 0}B x x= − > A B = 3( 3, )2 − − 3( 3, )2 − 3(1, )2 3( ,3)2 所以 ，故选 C. 3. 【2018 高考新课标Ⅲ文数】设集合 ，则 ＝（ ） （A） （B） （C） （D） 【答案】C 【解析】 试题分析：由补集的概念，得 ，故选 C． 4.【2018 高考新课标 1 文数】设集合 , ,则 （ ） （A）{1,3} （B）{3,5} （C）{5,7} （D）{1,7} 【答案】B 【解析】 试题分析：集合 与集合 公共元素有 3,5, ,故选 B． 5.【2018 高考山东理数】设集合 则 =（ ） （A） （B） （C） （D） 【答案】C 【解析】 试题分析： ， ，则 ，选 C. 6.【2018 高考山东理数】已知直线 a，b 分别在两个不同的平面 α，β 内.则“直线a 和直线 b 相交”是“平面 α 和平面 β 相交”的（ ） （A）充分不必要条件 （B）必要不充分条件 （C）充要条件 （D）既不充分也不必要条件 【答案】A 【解析】 7. 【2018 高考浙江理数】命题“ ，使得 ”的否定形式是（ ） A． ，使得 B． ，使得 C． ，使得 D． ，使得 A B {0,1,2,3}= 2{ | 2 , }, { | 1 0},xA y y x B x x= = ∈ = − = yyA }11|{ <<−= xxB A B = ∞ （- 1，+ ） *x n∀ ∈ ∃ ∈，R N 2n x> *x n∀ ∈ ∃ ∈，R N 2n x< *x n∀ ∈ ∀ ∈，R N 2n x< *x n∃ ∈ ∃ ∈，R N 2n x< *x n∃ ∈ ∀ ∈，R N 2n x< {0,2,4,6,8,10}, {4,8}A B= = AB {4 8}, {0 2 6}，, {0 2 610}，，, {0 2 4 6 810}，，，，, C {0,2,6,10}AB = { }1,3,5,7A = { }2 5B x x=   A B = A B }5,3{=BA  【答案】D 【解析】 试题分析： 的否定是，的否定是 ， 的否定是 ．故选 D． 8.【2018 高考天津理数】设{ }是首项为正数的等比数列，公比为 q，则“q<0”是“对任意的正 整数 n， ”的（ ） A 充要条件 B 充分而不必要条件 C 必要而不充分条件 D 既不充分也不必要条件 【答案】C 【解析】 ∀ ∀ 2n x≥ 2n x< na 2 1 2 0n na a− + <