【数学】2019届一轮复习北师大版　数形结合思想学案 11页

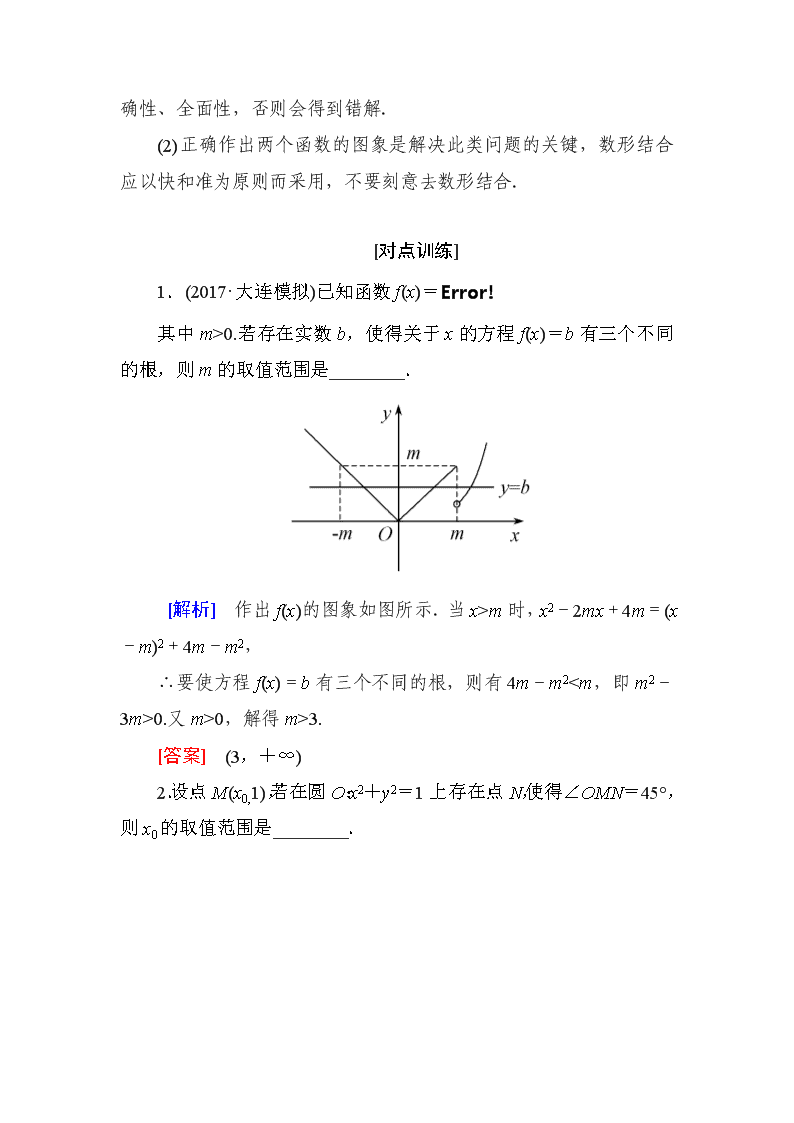
第二讲　数形结合思想 思想方法诠释 数形结合思想：是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的思想．通过“以形助数，以数辅形”，使复杂问题简单化，抽象问题具体化，能够变抽象思维为形象思维.‎ 要点一　利用数形结合思想研究函数的零点、‎ 方程的根、图象的交点问题 ‎[解析]　(1)函数f(x)＝lnx－x－a的零点，即关于x的方程lnx－x－a＝0的实根，将方程lnx－x－a＝0化为方程lnx＝x＋a，令y1＝lnx，y2＝x＋a，由导数知识可知，直线y2＝x＋a与曲线y1＝lnx相切时有a＝－1，如图所示，若关于x的方程lnx－x－a＝0有两个不同的实根，则实数a的取值范围是(－∞，－1)．故选B.‎ ‎(2)方程＝a|x|有三个不同的实数解等价于函数y＝与y＝a|x|的图象有三个不同的交点．在同一直角坐标系中作出函数y＝与y＝a|x|的图象，如图所示，由图易知，a>0.当－20.若存在实数b，使得关于x的方程f(x)＝b有三个不同的根，则m的取值范围是________．‎ ‎ [解析]　作出f(x)的图象如图所示．当x>m时，x2－2mx＋4m＝(x－m)2＋4m－m2，‎ ‎∴要使方程f(x)＝b有三个不同的根，则有4m－m20.又m>0，解得m>3.‎ ‎[答案]　(3，＋∞)‎ ‎2．设点M(x0,1)，若在圆O：x2＋y2＝1上存在点N，使得∠OMN＝45°，则x0的取值范围是________．‎ ‎[解析]　如图所示，由题意可知M在直线y＝1上运动，设直线y＝1与圆x2＋y2＝1相切于点P(0,1)．当x0＝0即点M与点P重合时，显然圆上存在点N(±1,0)符合要求；当x0≠0时，过M作圆的切线，切点之一为点P，此时对于圆上任意一点N，都有∠OMN≤∠OMP，故要存在∠OMN＝45°，只需∠OMP≥45°.特别地，当∠OMP＝45°时，有x0＝±1.结合图形可知，符合条件的x0的取值范围为[－1，1]．‎ ‎[答案]　[－1,1]‎ 要点二　利用数形结合思想解决最值问题 ‎[解析]　(1)作出不等式组对应的可行域，如图中阴影部分所示．易求得可行域的顶点A(0,1)，B(－6，－3)，C(6，－3)，平移直线y＝－2x＋z，当直线y＝－2x＋z过点B(－6，－3)时，z取得最小值，zmin＝2×(－6)－3＝－15，选择A.‎ ‎(2)根据题意，画出示意图，如图所示，则圆心C 的坐标为(3,4)，半径r＝1，且|AB|＝2m，因为∠APB＝90°，连接OP，易知|OP|＝|AB|＝m.要求m的最大值，即求圆C上的点P到原点O的最大距离．‎ 因为|OC|＝＝5，‎ 所以|OP|max＝|OC|＋r＝6，即m的最大值为6，故选B.‎ ‎[答案]　(1)A　(2)B 利用数形结合思想解决最值问题的3点思路 ‎(1)对于几何图形中的动态问题，应分析各个变量的变化过程，找出其中的相互关系求解．‎ ‎(2)对于求最大值、最小值问题，先分析所涉及知识，然后画出相应图象，数形结合求解．‎ ‎(3)如果(不)等式、代数式的结构蕴含着明显的几何特征，就要考虑用数形结合的思想方法来解题，即所谓的几何法求解．‎ ‎[对点训练]‎ ‎3．(2017·石家庄市高三二检)在平面直角坐标系中，不等式组(r为常数)表示的平面区域的面积为π，若x，y满足上述约束条件，则z＝‎ 的最小值为(　　)‎ A．－1　　　B．－　　　C.　　　D．－ ‎[解析]　作出不等式组表示的平面区域，如图中阴影部分所示，由题意，知πr2＝π，解得r＝2.z＝＝1＋，表示可行域内的点与点P(－3,2)连线的斜率加上1，由图知当可行域内的点与点P的连线与圆相切时斜率最小．设切线方程为y－2＝k(x＋3)，即kx－y＋3k＋2＝0，则有＝2，解得k＝－或k＝0(舍去)，所以zmin＝1－＝－.故选D.‎ ‎[答案]　D ‎4．(2017·武汉二模)已知抛物线的方程为x2＝8y，F是其焦点，点A(－2,4)，在此抛物线上求一点P，使△APF的周长最小，此时点P的坐标为________．‎ ‎[解析]　因为(－2)2<8×4，所以点A(－2,4)在抛物线x2＝8y的内部，‎ 如图，设抛物线的准线为l，‎ 过点P作PQ⊥l于点Q，过点A作AB⊥l于点B，连接AQ，由抛物线的定义可知△APF的周长为|PF|＋|PA|＋|AF|＝|PQ|＋|PA|＋|AF|≥|AQ|＋|AF|≥|AB|＋|AF|，‎ 当且仅当P，B，A三点共线时，△APF的周长取得最小值，即|AB|＋|AF|.‎ 因为A(－2,4)，‎ 所以不妨设△APF的周长最小时，点P的坐标为(－2，y0)，‎ 代入x2＝8y，得y0＝，‎ 故使△APF的周长最小的抛物线上的点P的坐标为 ，故填.‎ ‎[答案]　 要点三　利用数形结合思想解决不等式、参数问题 ‎[解析]　(1)曲线方程可转化为(x－2)2＋(y－3)2＝4(1≤y≤‎ ‎3)，即表示圆心为(2,3)，半径为2的下半圆，如图，依据数形结合，当直线y＝x＋b与此半圆相切时，圆心(2,3)到直线y＝x＋b的距离等于2，∴＝2，解得b＝1＋2或b＝1－2，因为是下半圆，所以b＝1－2；当直线过(0,3)时，可得b＝3，所以1－2≤b≤3.故选C.‎ ‎(2)对任意x∈R，都有f(x)≤|k－1|成立，即f(x)max≤|k－1|.‎ 因为f(x)的草图如图所示，‎ 观察f(x)＝的图象可知，当x＝时，函数f(x)max＝，所以|k－1|≥，解得k≤或k≥.‎ ‎[答案]　(1)C　∪ 利用数形结合思想解不等式或求参数范围问题的技巧 求参数范围或解不等式问题时经常联系函数的图象，根据不等式中量的特点，选择适当的两个(或多个)函数，利用两个函数图象的上、下位置关系转化数量关系来解决问题，往往可以避免繁琐的运算，获得简捷的解答．‎ ‎[对点训练]‎ ‎5．(2017·河南郑州月考)使log2(－x)