【数学】2020届数学文一轮复习第八章第1讲空间几何体的结构特征及三视图和直观图作业 8页

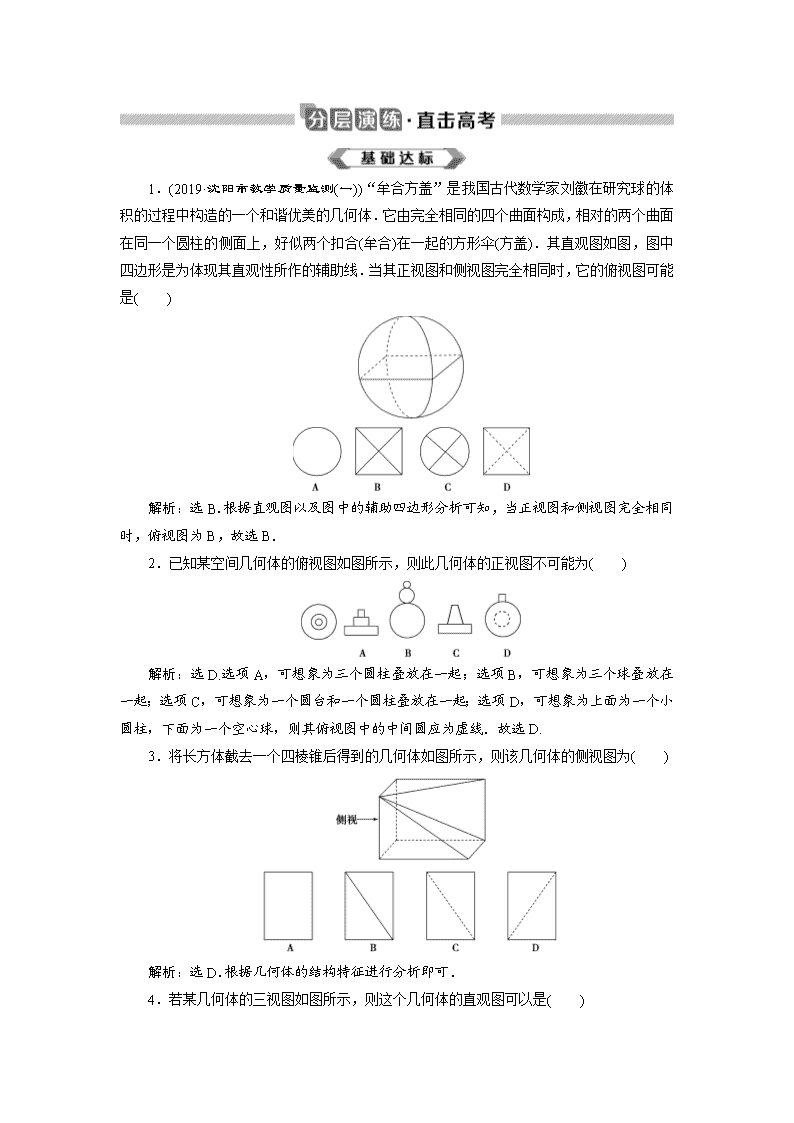
‎1．(2019·沈阳市教学质量监测(一))“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合(牟合)在一起的方形伞(方盖)．其直观图如图，图中四边形是为体现其直观性所作的辅助线．当其正视图和侧视图完全相同时，它的俯视图可能是(　　)‎ 解析：选B.根据直观图以及图中的辅助四边形分析可知，当正视图和侧视图完全相同时，俯视图为B，故选B.‎ ‎2．已知某空间几何体的俯视图如图所示，则此几何体的正视图不可能为(　　)‎ 解析：选D.选项A，可想象为三个圆柱叠放在一起；选项B，可想象为三个球叠放在一起；选项C，可想象为一个圆台和一个圆柱叠放在一起；选项D，可想象为上面为一个小圆柱，下面为一个空心球，则其俯视图中的中间圆应为虚线．故选D.‎ ‎3．将长方体截去一个四棱锥后得到的几何体如图所示，则该几何体的侧视图为(　　)‎ 解析：选D.根据几何体的结构特征进行分析即可．‎ ‎4．若某几何体的三视图如图所示，则这个几何体的直观图可以是(　　)‎ 解析：选D.A，B的正视图不符合要求，C的俯视图显然不符合要求，故选D.‎ ‎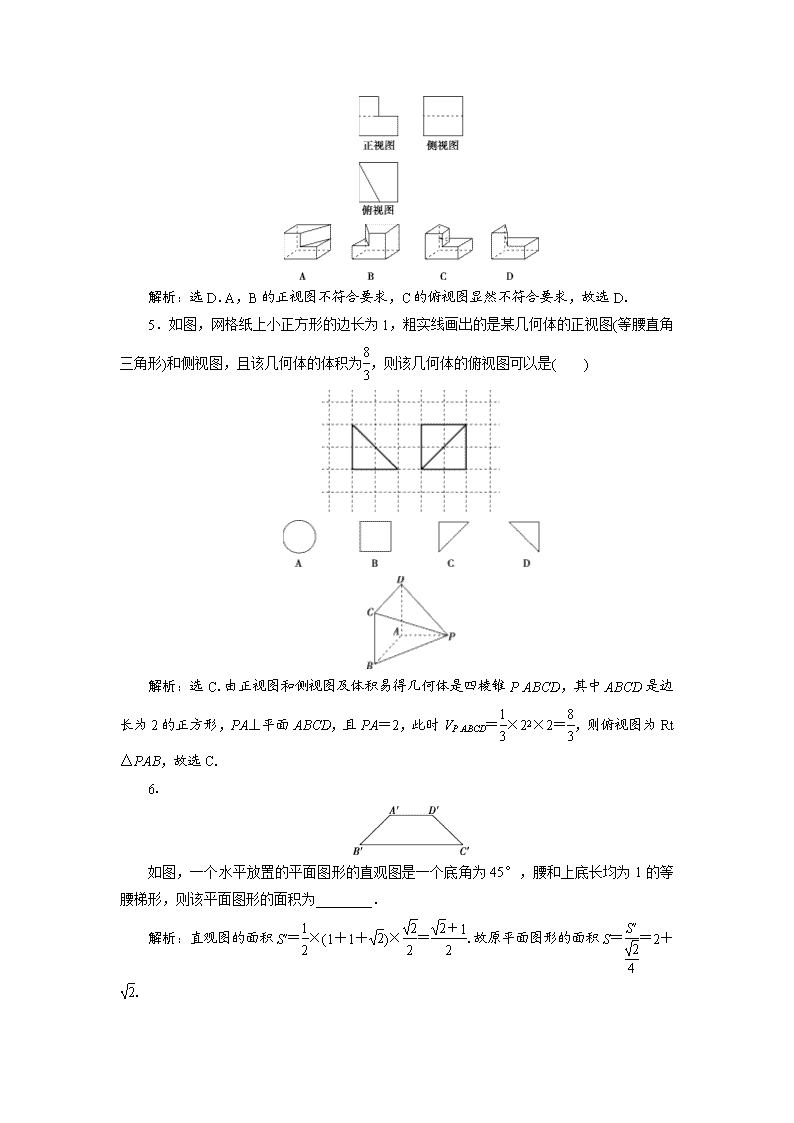5．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的正视图(等腰直角三角形)和侧视图，且该几何体的体积为，则该几何体的俯视图可以是(　　)‎ 解析：选C.由正视图和侧视图及体积易得几何体是四棱锥PABCD，其中ABCD是边长为2的正方形，PA⊥平面ABCD，且PA＝2，此时VPABCD＝×22×2＝，则俯视图为Rt△PAB，故选C.‎ ‎6.‎ 如图，一个水平放置的平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形，则该平面图形的面积为________．‎ 解析：直观图的面积S′＝×(1＋1＋)×＝.故原平面图形的面积S＝＝2＋.‎ 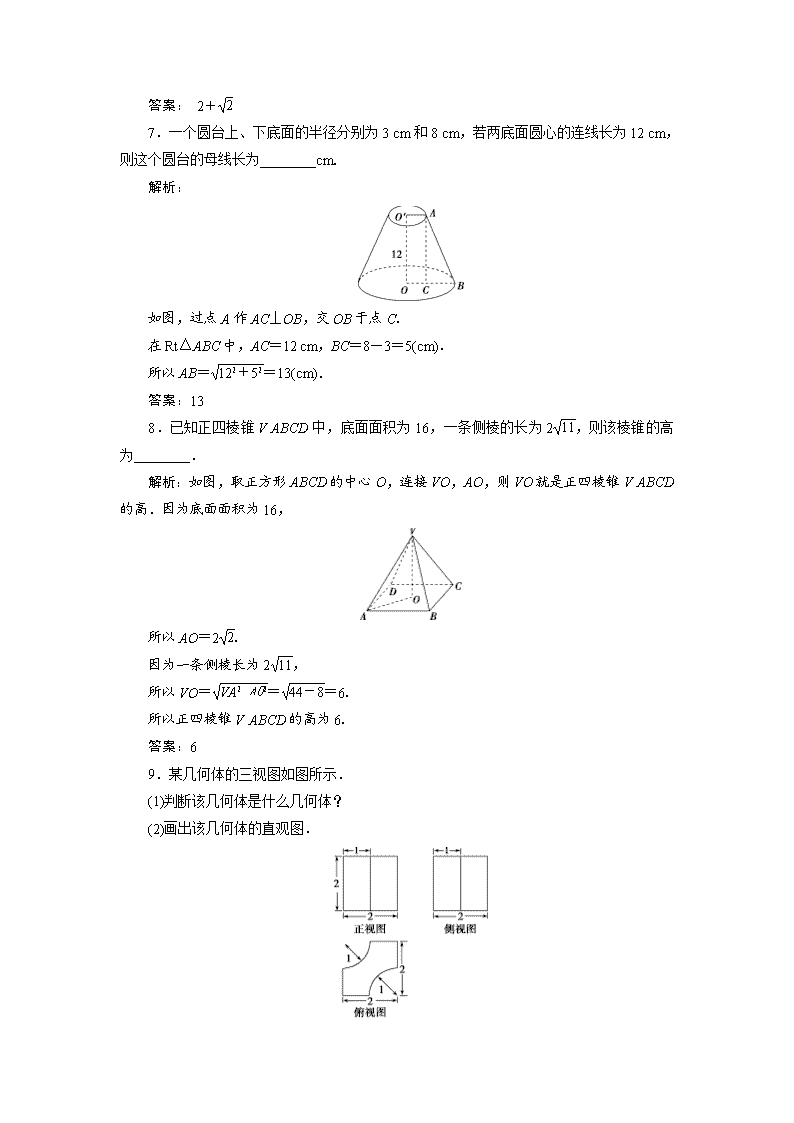答案： 2＋ ‎7．一个圆台上、下底面的半径分别为3 cm和8 cm，若两底面圆心的连线长为12 cm，则这个圆台的母线长为________cm.‎ 解析：‎ 如图，过点A作AC⊥OB，交OB于点C.‎ 在Rt△ABC中，AC＝12 cm，BC＝8－3＝5(cm)．‎ 所以AB＝＝13(cm)．‎ 答案：13‎ ‎8．已知正四棱锥VABCD中，底面面积为16，一条侧棱的长为2，则该棱锥的高为________．‎ 解析：如图，取正方形ABCD的中心O，连接VO，AO，则VO就是正四棱锥VABCD的高．因为底面面积为16，‎ 所以AO＝2.‎ 因为一条侧棱长为2，‎ 所以VO＝＝＝6.‎ 所以正四棱锥VABCD的高为6.‎ 答案：6‎ ‎9．某几何体的三视图如图所示．‎ ‎(1)判断该几何体是什么几何体？‎ ‎(2)画出该几何体的直观图．‎ 解：(1)该几何体是一个正方体切掉两个圆柱后得到的几何体．‎ ‎(2)直观图如图所示．‎ ‎10．如图所示的三个图中，上面是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图如图所示(单位：cm)．‎ ‎(1)在正视图下面，按照画三视图的要求画出该多面体的俯视图；‎ ‎(2)按照给出的尺寸，求该多面体的体积．‎ 解：(1)如图．‎ ‎(2)所求多面体的体积V＝V长方体－V正三棱锥 ‎＝4×4×6－×(×2×2)×2＝(cm3)．‎ ‎1．已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边长为2的直角三角形，则该三棱锥的正视图可能为(　　)‎ 解析：选C.当正视图为等腰三角形时，则高应为2，且应为虚线，排除A，D；当正视图是直角三角形，由条件得一个直观图如图所示，中间的线是看不见的线PA形成的投影，应为虚线，故答案为C.‎ ‎2．(2019·兰州适应性考试)如图，在正方体ABCDA1B1C1D1中，点P是线段A1C1上的动点，则三棱锥PBCD的俯视图与正视图面积之比的最大值为(　　)‎ A．1　　　　　　　 B. C. D．2‎ 解析：选D.正视图，底面B，C，D三点，其中D与C重合，随着点P的变化，其正视图均是三角形且点P在正视图中的位置在边B1C1上移动，由此可知，设正方体的棱长为a，则S正视图＝×a2；设A1C1的中点为O，随着点P的移动，在俯视图中，易知当点P在OC1上移动时，S俯视图就是底面三角形BCD的面积，当点P在OA1上移动时，点P越靠近A1，俯视图的面积越大，当到达A1的位置时，俯视图为正方形，此时俯视图的面积最大，S俯视图＝a2，所以的最大值为＝2，故选D.‎ ‎3．(2019·合肥第二次质量检测)如图，在正方体ABCDA1B1C1D1中，E是棱A1B1的中点，用过点A，C，E的平面截正方体，则位于截面以下部分的几何体的侧(左)视图为(　　)‎ 解析：选A.如图，取B1C1的中点为F，连接AC，CF，EF，AE，截面AEFC以下部分为所求得的几何体，易知选项A中的图形为其侧视图，故选A.‎ ‎4．如图是一个几何体的三视图，则该几何体任意两个顶点间距离的最大值是________．‎ 解析：作出直观图如图所示，通过计算可知AF、DC最长且DC＝AF＝＝3.‎ 答案：3 ‎5．如图，在四棱锥PABCD中，底面为正方形，PC与底面ABCD垂直，如图为该四棱锥的正视图和侧视图，它们是腰长为6 cm的全等的等腰直角三角形．‎ ‎(1)根据图中所给的正视图、侧视图，画出相应的俯视图，并求出该俯视图的面积；‎ ‎(2)求PA.‎ 解：(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形，如图，其面积为36 cm2.‎ 俯视图 ‎(2)由侧视图可求得PD＝＝＝6 (cm)．　‎ 由正视图可知AD＝6 cm，且AD⊥PD，‎ 所以在Rt△APD中，‎ PA＝＝　＝6 (cm)．‎ ‎6．已知正三棱锥VABC的正视图和俯视图如图所示．‎ ‎(1)画出该三棱锥的直观图和侧视图．‎ ‎(2)求出侧视图的面积．‎ 解：(1)如图．‎ ‎(2)侧视图中 VA＝ ‎＝＝2.‎ 则S△VBC＝×2×2＝6.‎