人教A版高中数学2-3幂函数教案新人教版必修1 5页

2.3 幂函数（教学设计） 教学目的： 1．通过实例，了解幂函数的概念． 2．具体结合函数 12 1 32 ,,,,  xyxyxyxyxy 的图象，了解幂函数的变化情况． 3．在归纳五个幂函数的基本性质时，应注意引导学生类比前面研究一般的函数、指数函数、对函数等过程中 的思想方法，对研究这些函数的思路作出指导． 教学重点：从五个具体的幂函数中认识幂函数的一些性质． 教学难点：画五个幂函数的图象并由图象概括其性质是教学中可能遇到的困难． 一、新课导入 先看五个具体的问题： （1）如果张红购买了每千克 1 元的蔬菜 w 千克，那么她需要支付 p=w 元，这里 p 是 w 的函数； （2）如果正方形的边长为 a，那么正方形的面积 2aS  ，这里 S 是 a 的函数； （3）如果立方体的边长为 a，求立方体的体积 3aV  ，这里V 是 a 的函数； （4）如果一个正方形场地的面积为 S ，那么这个正方形的边长 2 1 Sa  ，这里 a 是 S 的函数； （5）如果某人t s 内骑车进行了 1km，那么他骑车的平均速度 1 tv km/s，这里 v 是t 的函数． 讨论：以上五个问题中的函数具有什么共同特征？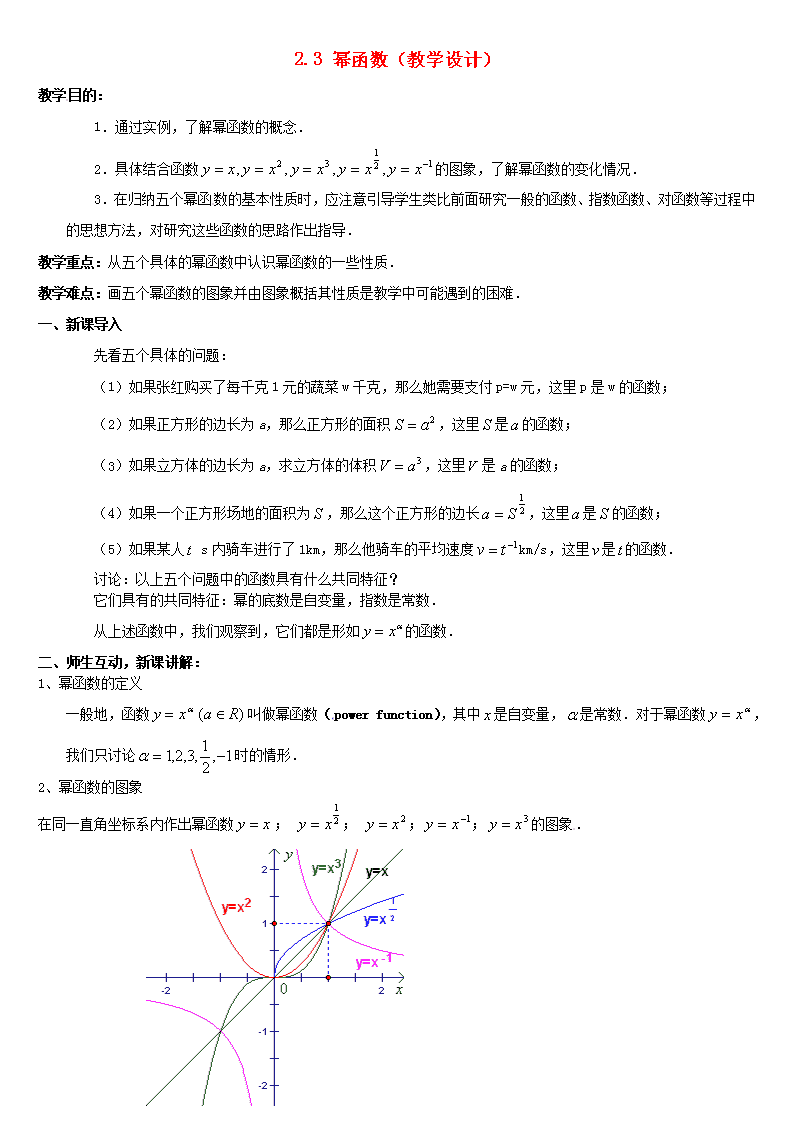 它们具有的共同特征：幂的底数是自变量，指数是常数． 从上述函数中，我们观察到，它们都是形如 y x 的函数． 二、师生互动，新课讲解： 1、幂函数的定义 一般地，函数 xy  )( Ra  叫做幂函数（power function），其中 x 是自变量， 是常数．对于幂函数 xy  ， 我们只讨论 1,2 1,3,2,1  时的情形． 2、幂函数的图象 在同一直角坐标系内作出幂函数 xy  ； 2 1 xy  ； 2xy  ； 1 xy ； 3xy  的图象． 观察以上函数的图象的特征，归纳出幂函数的性质． 3、幂函数的性质 1）．五个具体的幂函数的性质 （1）函数 xy  ； 2 1 xy  ； 2xy  ； 3xy  和 1 xy 的图象都通过点（1，1）； （2）函数 xy  ； 3xy  ； 1 xy 是奇函数，函数 2xy  是偶函数； （3）在区间 ),0(  上，函数 xy  ， 2xy  ， 3xy  和 2 1 xy  是增函数，函数 1 xy 是减函数； （4）在第一象限内，函数 1 xy 的图象向上与 y 轴无限接近，向右与 x 轴无限接近． 2）．一般的幂函数的性质 （1）所有的幂函数 xy  在（0，+∞）都有定义，并且图象都过点（1，1）； （2） 0 时，幂函数的图象通过原点，并且在区间 ),0[  上是增函数；  >1 时，图象向上，靠近 y 轴； 0< <1，图景向上，靠近 x 轴；  =1 是条直线。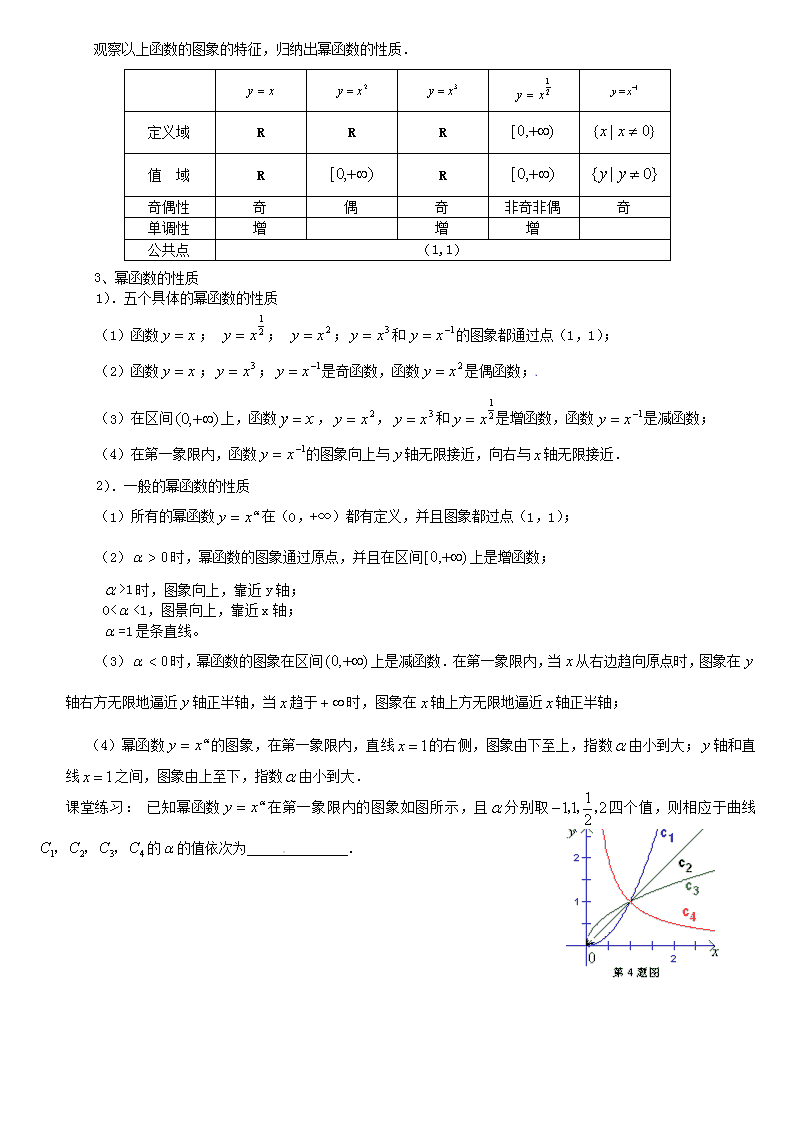 （3） 0 时，幂函数的图象在区间 ),0(  上是减函数．在第一象限内，当 x 从右边趋向原点时，图象在 y 轴右方无限地逼近 y 轴正半轴，当 x 趋于  时，图象在 x 轴上方无限地逼近 x 轴正半轴； （4）幂函数 xy  的图象，在第一象限内，直线 1x  的右侧，图象由下至上，指数 由小到大； y 轴和直 线 1x  之间，图象由上至下，指数 由小到大． 课堂练习： 已知幂函数 xy  在第一象限内的图象如图所示，且 分别取 111 22  ，，，四个值，则相应于曲线 1 2 3 4C C C C， ， ， 的 的值依次为 ． xy  2xy  3xy  2 1 xy  1xy 定义域 R R R ),0[  }0|{ xx 值 域 R ),0[  R ),0[  }0|{ yy 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增 增 增 公共点 （1,1） 例 1：（课本第 78 页例 1）证明幂函数 xxf )( 在 ),0[  上是增函数． 变式训练 1：利用幂函数的性质，比较下列各题中两个幂的值的大小： （1） 4 3 3.2 ， 4 3 4.2 ；（2） 5 6 31.0 ， 5 6 35.0 ；（3） 2 3 )2(  ， 2 3 )3(  ；（4） 2 1 1.1  ， 2 1 9.0  ． 例 2：求下列函数的定义域，并判断它们的奇偶性： （1） 3y x ；（2） 2y x ；（3） 1 2y x ； （4） 1 3y x 解 （1）函数 3y x 的定义域是 R ，它是奇函数； （2）函数 2y x 即 2 1y x  ，其定义域是 ( ,0) (0, )  ，它是偶函数； （3）函数 1 2y x 即 y x ，其定义域是[0, ) ，它既不是奇函数，也不是偶函数； （4）函数 1 3y x 即 3y x ，其定义域是 R ，它是奇函数． 变式训练 2： （1）. 设 111 32a      ，，， ，则使函数 ay x 的定义域为 R 且为奇函数的所有 a 值为（ A ）． (A) 1，3 (B) 1 ，1 (C) 1 ，3 (D) 1 ，1，3 （2）. 若函数 3( ) ( )f x x x  R ，则函数 ( )y f x  在其定义域上是（ B ）． (A) 单调递减的偶函数 (B) 单调递减的奇函数 (C) 单调递增的偶函数 (D) 单调递增的奇函数 （3）若幂函数 f(x)的图象经过点(3，1 9 )，则其定义域为( ) A．{x|x∈R，x>0} B．{x|x∈R，x<0}C．{x|x∈R，且 x≠0} D．R 解析：设 f(x)＝xα.∵图象过点(3，1 9 )，∴1 9 ＝3α，即 3－2＝3a，∴α＝－2，即 f(x)＝x－2＝1 x2，∴x2≠0，即 x≠0. 答案：C 例 3：在同一坐标系作出函数 y=x2 与 y=2x 的图象。 变式训练 3：已知幂函数 f(x)＝ (m∈N*)的图象关于 y 轴对称，且在(0，＋∞)上是减函 数，则实数 m＝ ________. 解析：∵幂函数 f(x)＝ 在(0，＋∞)上是减函数，∴m2－2m－3<0，∴－1(－1 5 )n，则 n＝__________. 解析：可以逐一进行检验，也可利用幂函数的单调性求解． 答案：－1 或 2 3．（课本 P79 习题 2.3 NO:1）已知幂函数 )(xfy  的图象过点 )2,2( ，试求出这个函数的解析式． 4．(课本 P79 习题 2.3 NO:2)在固定压力差（压力差为常数）下，当气体通过圆形管道时，其流量速率 v（单位：cm3/s） 与管道半径 r(单位：cm)的四次方成正比． （1）写出气流流量速率 v 关于管道半径 r 的函数解析式； （2）若气体在半径为 3cm 的管道中，流量速率为 400cm3/s，求该气体通过半径为 r 的管道时，其流量速率 v 的表 达式； （3）已知（2）中的气体通过的管道半径为 5cm，计算该气体的流量速率（精确到 1cm3/s）． 5．讨论函数 3 2 xy  的定义域、奇偶性，作出它的图象，并根据图象说出函数的单调性． 6．已知函数 f(x)＝2 x －xm，且 f(4)＝－7 2 . (1)求 m 的值； (2)判断 f(x)在(0，＋∞)上的单调性，并给予证明． 解：(1)∵f(4)＝－7 2 ，∴2 4 －4m＝－7 2 .∴m＝1. (2)f(x)＝2 x －x 在(0，＋∞)上单调递减， 证明如下： 任取 00， 2 x1x2 ＋1>0. ∴f(x1)－f(x2)>0，∴f(x1)>f(x2)， 即 f(x)＝2 x －x 在(0，＋∞)上单调递减． B 组： 1．如果幂函数 f(x)＝ (p∈Z)是偶函数．且在(0，＋∞)上是增函数．求 p 的值，并写出相应的 函数 f(x)的解析式． 解析：∵f(x)在(0，＋∞)上是增函数，∴－1 2 p2＋p＋3 2 >0，即 p2－2p－3<0.∴－1