- 77.00 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2019届一轮复习苏教版 几种常见的平面变换 学案
本章在高考中主要考查对六种特殊变换的理解,以及在六种变换前后的点的坐标及曲线方程的求法,掌握六种特殊变换的特点.
一、求在某种变换作用下得到的图形(表达式)
求在某种变换作用下所得到的图形(表达式)是考查变换知识的热点题型,通常用代入法(相关点法)求解.
下列所给的矩阵将给定的图形变成了什么图形?画图并指出该变换是什么变换?
(1),点A(2,1);
(2),直线y=2x+2.
【解】 (1)矩阵对应的坐标变换公式为把A(2,1)代入即得A的对应点为A′(1,-2),该变换把列向量=按顺时针方向旋转90°.故该变换为旋转变换,如图所示.
(2)设直线y=2x+2上任意一点P(x,y)按矩阵所表示的坐标变换对应的点为P′(x′,y′),
则==,即
∴代入y=2x+2,
得-y′=2x′+2,即直线y=2x+2经过变换得到的图形为直线y=-2x-2,如图所示,此变换为关于x轴的反射变换.
二、求变换矩阵
根据变换的结果求变换矩阵的一般方法:找到前后点的坐标间的关系,由点的坐标间的关系即可求出变换矩阵.
求把△ABC变换成△A′B′C′的变换对应的矩阵,其中A(-2,1),B(0,1),C(0,-1);A′(-2,-3),B′(0,1),C′(0,-1).
【解】 设变换对应的矩阵为,
由已知,得=,
=,
=,
即
即
∴变换对应的矩阵为.
三、函数方程思想
本章求矩阵变换下曲线的方程广泛应用了函数方程思想.
试讨论下列矩阵将所给图形变成了什么图形,并指出该变换是什么变换.
(1),图形的方程为:x2+y2=4;
(2),图形的方程为:y=-2x+6.
【解】 (1)所给方程表示的是以原点为圆心,2为半径的圆.设A(x,y)为曲线上的任意一点,经过变换后的点为A1(x1,y1),则==,
∴2x=x1,y=y1,即x=,y=y1
将其代入x2+y2=4可得到方程+y=4,此方程表示椭圆.
所给方程表示的是圆,该变换是伸压变换.
(2)所给方程表示的是一条直线.设A(x,y)为直线上的任意一点,经过变换后的点为A1(x1,y1).
∵==,
∴x1=0,y1=2x+y.
又由y=-2x+6得2x+y=6,
∴A1(0,6)为定点.
通过变换将一条直线变为一点,该变换是投影变换.
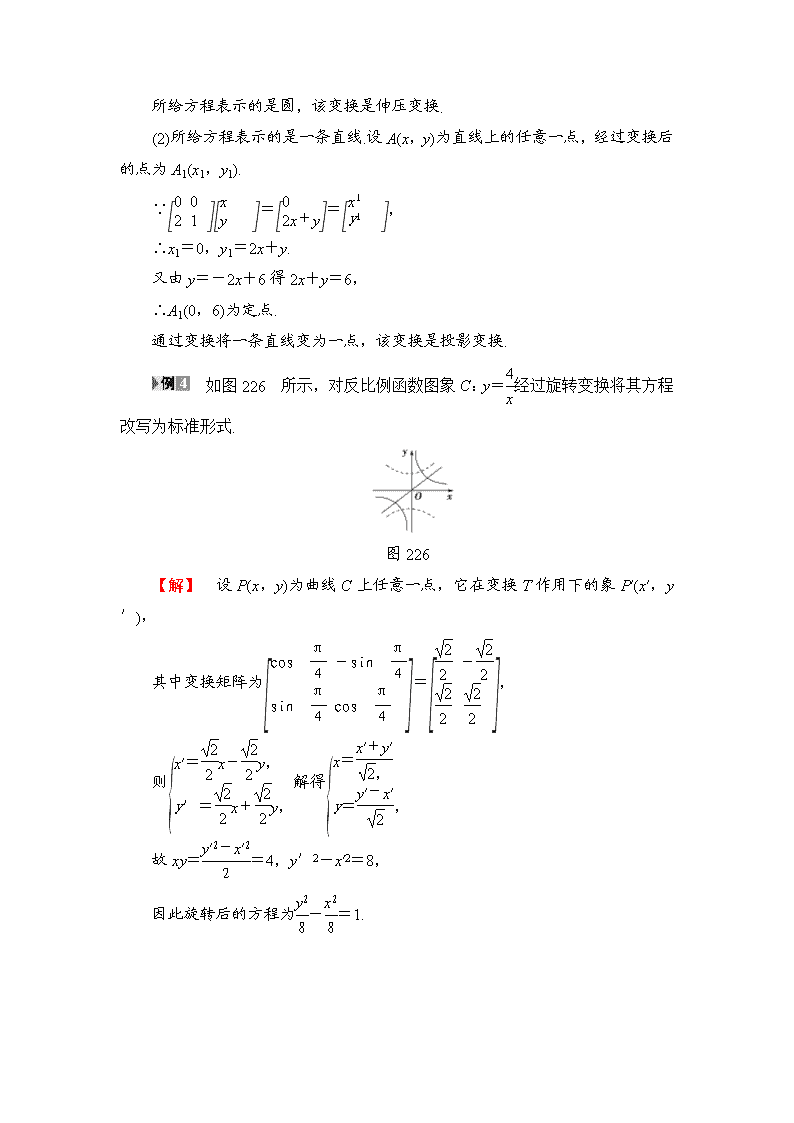
如图226所示,对反比例函数图象C:y=经过旋转变换将其方程改写为标准形式.
图226
【解】 设P(x,y)为曲线C上任意一点,它在变换T作用下的象P′(x′,y′),
其中变换矩阵为=,
则解得
故xy==4,y′2-x′2=8,
因此旋转后的方程为-=1.