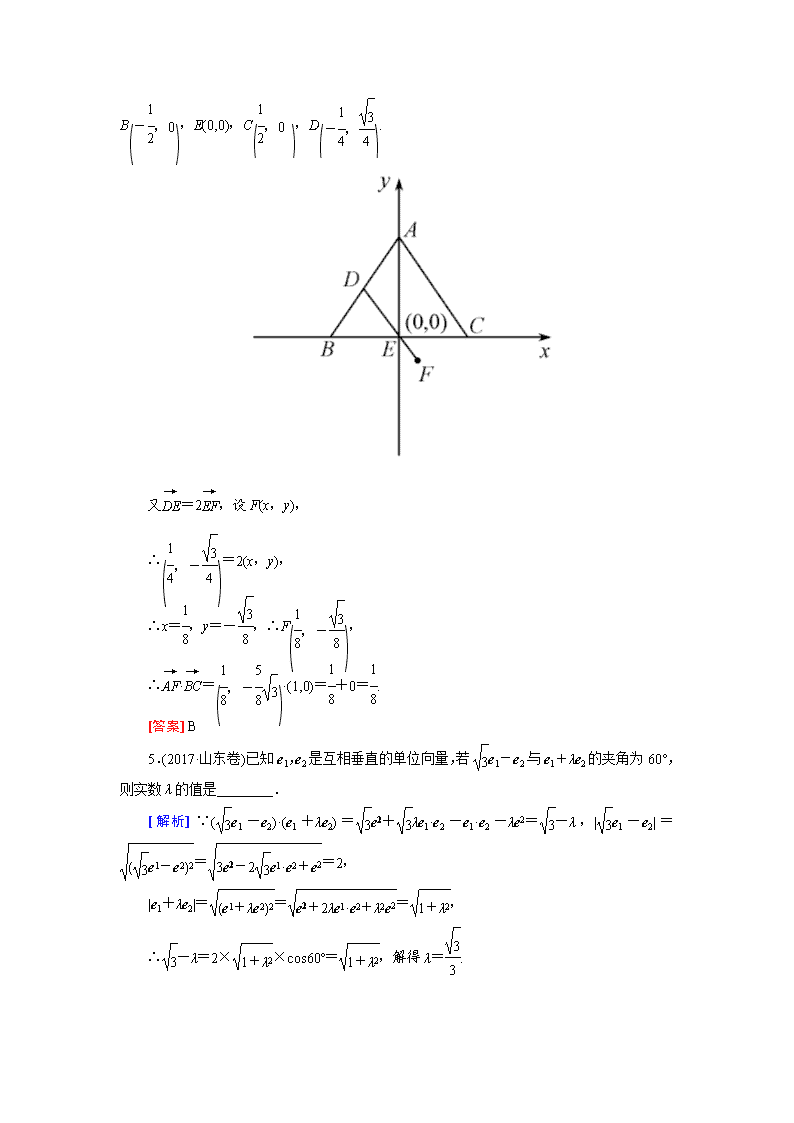【数学】2019届一轮复习北师大版 平面向量 学案 13页

专题二 三角函数、平面向量 第三讲 平面向量 高考导航 平面向量的基本定理及基本运算，即向量的有关概念，加、减法的几何意义，线性表示以及坐标运算等．‎ ‎2．平面向量的数量积的基本运算及其应用，这也是历年高考命题的热点．‎ ‎3．向量的工具性作用，在三角函数、不等式、解析几何解答题中用来描述题目的条件和结论.‎ ‎1．(2016·全国卷Ⅱ)已知向量a＝(1，m)，b＝(3，－2)，且(a＋b)⊥b，则m＝( )‎ A．－8 B．－6‎ C．6 D．8‎ ‎[解析] 由题可得a＋b＝(4，m－2)，又(a＋b)⊥b，∴4×3－2×(m－2)＝0，∴m＝8.故选D.‎ ‎[答案] D ‎2．(2015·山东卷)已知菱形ABCD的边长为a，∠ABC＝60°，则·＝( )‎ A．－a2 B．－a2‎ C.a2 D.a2‎ ‎[解析] ∵＝＋，且＝，‎ ‎∴·＝(＋)· ‎＝·＋2‎ ‎＝||||cos60°＋||2‎ ‎＝a2＋a2＝a2.故选D.‎ ‎[答案] D ‎3．(2017·福建龙岩二模)已知向量与的夹角为60°，且||＝3，||＝2，若＝m＋n，且⊥，则实数的值为( )‎ A. B. C．6 D．4‎ ‎[解析] 由题意知·＝3×2×cos60°＝3.又∵＝m＋n，⊥，∴·＝(m＋n)·(－)＝n2＋(m－n)·－m2＝0，又∵||＝3，||＝2，·＝3，∴4n＋3(m－n)－‎9m＝n－‎6m＝0，∴＝.故选A.‎ ‎[答案] A ‎4．(2016·天津卷)已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE＝2EF，则·的值为( )‎ A．－ B. C. D. ‎[解析] 解法一：∵＝－，‎ ＝＋＝＋＝＋，‎ ‎∴·＝(－) ‎＝×1×1×－＋－×1×1×＝－＋－＝，选B.‎ 解法二：以BC为x轴，E为坐标原点建立如图所示平面直角坐标系，易知A，B，E(0,0)，C，D.‎ 又＝2，设F(x，y)，‎ ‎∴＝2(x，y)，‎ ‎∴x＝，y＝－，∴F，‎ ‎∴·＝·(1,0)＝＋0＝.‎ ‎[答案] B ‎5．(2017·山东卷)已知e1，e2是互相垂直的单位向量，若e1－e2与e1＋λe2的夹角为60°，则实数λ的值是________．‎ ‎[解析] ∵(e1－e2)·(e1＋λe2)＝e＋λe1·e2－e1·e2－λe＝－λ，|e1－e2|＝＝＝2，‎ ‎|e1＋λe2|＝＝＝，‎ ‎∴－λ＝2××cos60°＝，解得λ＝.‎ ‎[答案] 考点一 平面向量的概念及线性运算 ‎1．在平面向量的化简或运算中，要根据平面向量基本定理选好基底，变形要有方向不能盲目转化．‎ ‎2．在用三角形加法法则时要保证“首尾相接”‎ ‎，结果向量是第一个向量的起点指向最后一个向量的终点所在的向量；在用三角形减法法则时要保证“同起点”，结果向量的方向是指向被减向量．‎ ‎[对点训练]‎ ‎1．(2017·唐山模拟)在等腰梯形ABCD中，＝－2，M为BC的中点，则＝( )‎ A.＋ B.＋ C.＋ D.＋ ‎[解析] 因为＝－2，所以＝2.又M是BC的中点，所以＝(＋)＝(＋＋)＝＝＋，故选B.‎ ‎[答案] B ‎2．(2017·河北三市联考)已知e1，e2是不共线向量，a＝me1＋2e2，b＝ne1－e2，且mn≠0，若a∥b，则等于( )‎ A．－ B. C．－2 D．2‎ ‎[解析] ∵a∥b，∴a＝λb，即me1＋2e2＝λ(ne1－e2)，则故＝－2.‎ ‎[答案] C ‎3．(2017·河南郑州质检)已知P为△ABC所在平面内一点，D为AB的中点，若2＋＝(λ＋1)＋，且 ‎△PBA与△PBC的面积相等，则实数λ的值为________．‎ ‎[解析] ∵D为AB的中点，∴2＝＋，‎ 又∵2＋＝(λ＋1)＋.‎ ‎∴＋＋＝(λ＋1)＋ ‎∴＝λ，又△PBA与△PBC的面积相等，‎ ‎∴P为AC的中点，∴λ＝－1.‎ ‎[答案] －1‎ ‎4．(2017·盐城一模)在△ABC中，∠A＝60°，∠A的平分线交BC于点D，若AB ‎＝4，且＝＋λ(λ∈R)，则AD的长为________．‎ ‎[解析] ‎ 因为B，D，C三点共线，所以＋λ＝1，解得λ＝，如图，过点D分别作AC，AB的平行线交AB，AC于点M，N，则＝，＝，经计算得AN＝AM＝3，AD＝3.‎ ‎[答案] 3 ‎ 平面向量线性运算的2种技巧 ‎(1)对于平面向量的线性运算问题，要尽可能转化到三角形或平行四边形中，灵活运用三角形法则、平行四边形法则，紧密结合图形的几何性质进行运算．‎ ‎(2)在证明两向量平行时，若已知两向量的坐标形式，常利用坐标运算来判断；若两向量不是以坐标形式呈现的，常利用共线向量定理(当b≠0时，a∥b⇔存在唯一实数λ，使得a＝λb)来判断．‎ 考点二 平面向量的数量积 ‎1．平面向量的数量积有两种运算形式 ‎(1)数量积的定义：a·b＝|a||b|cosθ(其中θ为向量a，b的夹角)．‎ ‎(2)坐标运算：a＝(x1，y1)，b＝(x2，y2)时，a·b＝x1x2＋y1y2.‎ ‎2．投影 向量a在向量b方向上的投影为＝|a|cosθ(θ为向量a，b的夹角)．‎ ‎[对点训练]‎ ‎1．(2017·重庆适应性测试)已知非零向量a，b的夹角为，且|b|＝1，|b－‎2a|＝1，则|a|＝( )‎ A. B．1 C. D．2‎ ‎[解析] 依题意得(b－‎2a)2＝1，即b2＋‎4a2－‎4a·b＝1,1＋4|a|2－2|a|＝1,4|a|2－2|a|＝0(|a|≠0)，因此|a|＝，选A.‎ ‎[答案] A ‎2．(2017·陕西省西安地区高三八校联考)已知点A(－1,1)，B(1,2)，C(－2，－1)，D(3,4)，则向量在方向上的投影是( )‎ A．－3 B．－ C．3 D. ‎[解析] 依题意得，＝(－2，－1)，＝(5,5)，·＝(－2，－1)·(5,5)＝－15，||＝，因此向量在方向上的投影是＝＝－3，选A.‎ ‎[答案] A ‎3．已知向量a，b满足|a|＝1，(a＋b)·(a－2b)＝0，则|b|的取值范围为( )‎ A．[1,2] B．[2,4]‎ C. D. ‎[解析] 由题意知b≠0，设向量a，b的夹角为θ，因为(a＋b)·(a－2b)＝a2－a·b－2b2＝0，又|a|＝1，所以1－|b|cosθ－2|b|2＝0，所以|b|cosθ＝1－2|b|2，因为－1≤cosθ≤1，所以－|b|≤1－2|b|2≤|b|，所以≤|b|≤1，所以|b|的取值范围是.‎ ‎[答案] D ‎4．在△ABC中，AD⊥AB，＝2 ，||＝1，则·＝________.‎ ‎[解析] 因为在△ABC中，＝2，所以·＝(＋)·＝(＋2)·，又＝－，所以·＝[(1－2)＋2 ]·＝(1－2)·＋2·＝(1－2)·＋22，因为AD⊥AB，所以·＝0，所以·＝(1－2)×0＋2×1＝2.‎ ‎[答案] 2 ‎ 平面向量数量积的两种运算方法 ‎(1)依据模和夹角计算，要注意确定这两个向量的夹角，如夹角不易求或者不可求，可通过选择易求夹角和模的基底进行转化．‎ ‎(2)利用坐标来计算，向量的平行和垂直都可以转化为坐标满足的等式，从而应用方程思想解决问题，化形为数，使向量问题数字化．‎ 考点三 平面向量的综合应用 ‎ 平面向量作为解决问题的工具，具有代数形式和几何形式的“双重型”，高考常在平面向量与三角函数、解三角形、解析几何等交汇处命题，通过向量运算作为题目条件．角度1：平面向量与解三角形 ‎[解析] 根据题意，由＝2＋，可得－＝＝2，则||＝2||＝4，由＝－，可得||2＝|－|2＝2－2·＋2＝4，故||＝2，由＝－＝(2＋)－＝＋，得||2＝|＋|2＝2＋2·＋2＝12，可得||＝2.在△ABC中，由||＝4，||＝2，||＝2，可得||2＝||2＋||2，则△ABC为直角三角形．故选C.‎ ‎[答案] C ‎[解析] ‎ 解法一：设BC的中点为D，AD的中点为E，则有＋＝2，‎ 则·(＋)＝2· ‎＝2(＋)·(－)＝2(2－2)．‎ 而2＝2＝，‎ 当P与E重合时，2有最小值0，故此时·(＋)取最小值，‎ 最小值为－22＝－2×＝－.‎ 解法二：‎ 以AB所在直线为x轴，AB的中点为原点建立平面直角坐标系，如图，‎ 则A(－1,0)，B(1,0)，C(0，)，设P(x，y)，取BC的中点D，则D.·(＋)＝2·＝2(－1－x，－y)·＝2＝2.‎ 因此，当x＝－，y＝时，·(＋)取得最小值，为2×＝－，故选B.‎ ‎[答案] B ‎ 解决平面向量综合问题的两种方法 ‎(1)基向量法：根据平面向量的基本定理，选好基向量，再把题目所给向量用基向量表示出来，最后翻译题目所给向量关系．‎ ‎(2)坐标法：在解决平面几何问题时，可通过建立平面直角坐标系将问题坐标化，然后利用平面向量的坐标运算求解有关问题，这样可以避免繁杂的逻辑推理，同时加强了数形结合思想在解题中的应用．‎ ‎ [对点训练]‎ ‎1．[角度1](2017·广州模拟)△ABC的三个内角A，B，C所对边长分别是a，b，c，设向量n＝(a＋c，sinB－sinA)，m＝(a＋b，sinC)，若m∥n，则角B的大小为( )‎ A. B. C. D. ‎[解析] 若m∥n，则 ‎(a＋b)(sinB－sinA)－(a＋c)sinC＝0，‎ 由正弦定理可得(a＋b)(b－a)－c(a＋c)＝0，化为a2＋c2－b2＝－ac，‎ ‎∴cosB＝＝－.‎ ‎∵B∈(0，π)，∴B＝.故选B.‎ ‎[答案] B ‎2．[角度2](2015·湖南卷)已知点A，B，C在圆x2＋y2＝1上运动，且AB⊥BC.若点P的坐标为(2,0)，则|＋＋|的最大值为( )‎ A．6 B．7 C．8 D．9‎ ‎[解析] 解法一：因为A，B，C均在单位圆上，AC为直径，故＋＝2＝(－4,0)，|＋＋|＝|2＋|≤2||＋||，又||≤||＋1＝3，所以|＋＋P|≤4＋3＝7，故其最大值为7，选B.‎ 解法二：因为A，B，C均在单位圆上，AC为直径，不妨设A(cosx，sinx)，B(cos(x＋α)，sin(x＋α))(α≠kπ，k∈ )，C(－cosx，－sinx)，＋＋＝(cos(x＋α)－6，sin(x＋α))，‎ ‎|＋＋|＝＝≤7，故选B.‎ ‎[答案] B 热点课题9 坐标法在平面向量中的应用 ‎ [感悟体验]‎ ‎1．(2017·福州二模)在等腰直角△ABC中，∠ABC＝90°，AB＝BC＝2，M，N为AC边上的两个动点(M，N不与A，C重合)，且满足||＝，则·的取值范围为( )‎ A. B. C. D. ‎[解析] ‎ 不妨设点M靠近点A，点N靠近点C，以等腰直角三角形ABC的直角边所在直线为坐标轴建立平面直角坐标系，如图所示，‎ 则B(0,0)，A(0,2)，C(2,0)，线段AC的方程为x＋y－2＝0(0≤x≤2)．设M(a,2－a)，N(a＋1,1－a)(由题意可知0