【数学】2019届一轮复习苏教版第4章三角函数解三角形第22讲学案 15页

第22讲　三角函数的图象和性质 考试要求　1.y＝sin x，y＝cos x，y＝tan x的图象及周期性(A级要求)；2正弦函数、余弦函数在区间[0，2π]上的性质(如单调性、最值及与x轴的交点等)(B级要求)；3.正切函数在区间内的单调性(B级要求).‎ 诊 断 自 测 ‎1.思考辨析(在括号内打“√”或“×”)‎ ‎(1)由sin＝sin 知，是正弦函数y＝sin x(x∈R)的一个周期.(　　)‎ ‎(2)余弦函数y＝cos x的对称轴是y轴.(　　)‎ ‎(3)正切函数y＝tan x在定义域内是增函数.(　　)‎ ‎(4)已知y＝ksin x＋1，x∈R，则y的最大值为k＋1.(　　)‎ ‎(5)y＝sin|x|是偶函数.(　　)‎ 解析　(1)函数y＝sin x的周期是2kπ(k∈ ).‎ ‎(2)余弦函数y＝cos x的对称轴有无穷多条，y轴只是其中的一条.‎ ‎(3)正切函数y＝tan x在每一个区间(k∈ )上都是增函数，但在定义域内不是单调函数，故不是增函数.‎ ‎(4)当k>0时，ymax＝k＋1；当k<0时，ymax＝－k＋1.‎ 答案　(1)×　(2)×　(3)×　(4)×　(5)√‎ ‎2.(2018·苏北四市一模)函数y＝cos的最小正周期为________.‎ 解析　函数y＝cos的最小正周期T＝＝4π.‎ 答案　4π ‎3.(必修4P33例4改编)函数y＝2tan的定义域为________.‎ 解析　∵x－≠kπ＋，k∈ ，∴x≠kπ＋，k∈ ，‎ 即函数的定义域为.‎ 答案　 ‎4.(2017·苏州一模)若函数f(x)＝sin(φ∈[0，2π])是偶函数，则φ＝________.‎ 解析　由已知f(x)＝sin是偶函数，可得＝kπ＋(k∈ )，即φ＝3kπ＋(k∈ )，又φ∈[0，2π]，‎ 所以φ＝.‎ 答案　 ‎5.函数f(x)＝sin在区间上的最小值为________.‎ 解析　由已知x∈，得2x－∈，所以sin∈，故函数f(x)＝sin在区间上的最小值为－.‎ 答案　－ 知 识 梳 理 ‎1.用五点法作正弦函数和余弦函数的简图 ‎(1)正弦函数y＝sin x，x∈[0，2π]的图象中，五个关键点是：(0，0)，，(π，0)，，(2π，0).‎ ‎(2)余弦函数y＝cos x，x∈[0，2π]的图象中，五个关键点是：(0，1)，，(π，－1)，，(2π，1).‎ ‎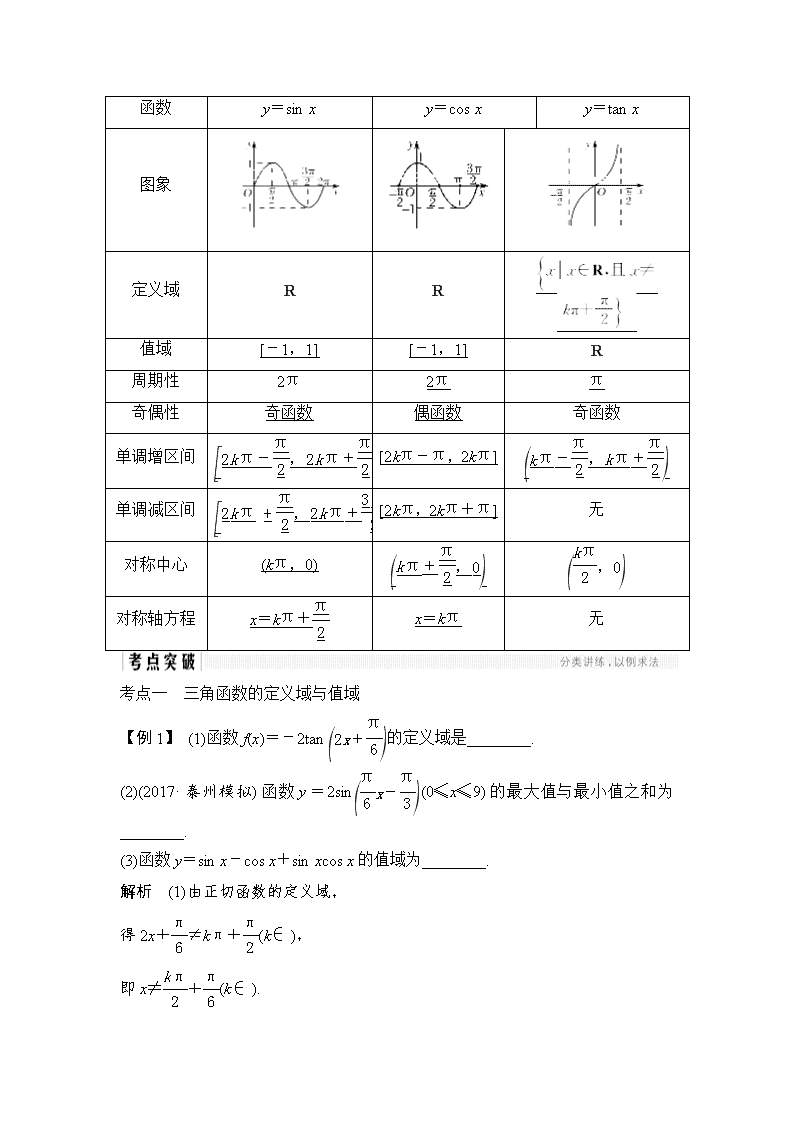2.正弦、余弦、正切函数的图象与性质(下表中k∈ )‎ 函数 y＝sin x y＝cos x y＝tan x 图象 定义域 R R 值域 ‎[－1，1]‎ ‎[－1，1]‎ R 周期性 ‎2π ‎2π π 奇偶性 奇函数 偶函数 奇函数 单调增区间 ‎[2kπ－π，2kπ]‎ 单调减区间 ‎[2kπ，2kπ＋π]‎ 无 对称中心 ‎(kπ，0)‎ 对称轴方程 x＝kπ＋ x＝kπ 无 考点一　三角函数的定义域与值域 ‎【例1】 (1)函数f(x)＝－2tan的定义域是________.‎ ‎(2)(2017·泰州模拟)函数y＝2sin(0≤x≤9)的最大值与最小值之和为________.‎ ‎(3)函数y＝sin x－cos x＋sin xcos x的值域为________.‎ 解析　(1)由正切函数的定义域，‎ 得2x＋≠kπ＋(k∈ )，‎ 即x≠＋(k∈ ).‎ ‎∴函数的定义域为.‎ ‎(2)因为0≤x≤9，所以－≤x－≤，‎ 所以sin∈.‎ 所以y∈[－，2]，所以ymax＋ymin＝2－.‎ ‎(3)设t＝sin x－cos x，‎ 则t2＝sin2x＋cos2x－2sin xcos x，‎ sin xcos x＝，且－≤t≤.‎ ‎∴y＝－＋t＋＝－(t－1)2＋1.‎ 当t＝1时，ymax＝1；‎ 当t＝－时，ymin＝－－.‎ ‎∴函数的值域为.‎ 答案　(1)　(2)2－ ‎(3) 规律方法　(1)三角函数定义域的求法，以正切函数为例，应用正切函数y＝tan x的定义域求函数y＝Atan(ωx＋φ)的定义域.‎ ‎(2)求解三角函数的值域(最值)常见到以下几种类型：‎ ‎①形如y＝asin x＋bcos x＋c的三角函数化为y＝Asin(ωx＋φ)＋c的形式，再求值域(最值)；‎ ‎②形如y＝asin2x＋bsin x＋c的三角函数，可先设sin x＝t，化为关于t的二次函数求值域(最值)；‎ ‎③形如y＝asin xcos x＋b(sin x±cos x)＋c的三角函数，可先设t＝sin x±cos x，化为关于t的二次函数求值域(最值).‎ ‎【训练1】 (1)函数y＝tan 2x的定义域是________.‎ ‎(2)(2016·全国Ⅱ卷改编)函数f(x)＝cos 2x＋6cos的最大值为________.‎ 解析　(1)由2x≠kπ＋，k∈ ，得x≠＋，k∈ ，‎ ‎∴y＝tan 2x的定义域为.‎ ‎(2)由f(x)＝cos 2x＋6cos＝1－2sin2x＋6sin x＝－2＋，所以当sin x＝1时函数的最大值为5.‎ 答案　(1)　(2)5‎ 考点二　三角函数的单调性 ‎【例2】 (1)函数f(x)＝sin的单调递减区间为________.‎ ‎(2)(一题多解)若f(x)＝2sin ωx＋1(ω>0)在区间上是增函数，则ω的取值范围是________.‎ 解析　(1)由已知可得函数为y＝－sin，欲求函数的单调减区间，只需求y＝sin的单调增区间.‎ 由2kπ－≤2x－≤2kπ＋，k∈ ，‎ 得kπ－≤x≤kπ＋，k∈ .‎ 故所求函数的单调递减区间为(k∈ ).‎ ‎(2)法一　由2kπ－≤ωx≤2kπ＋，k∈ ，‎ 得f(x)的增区间是(k∈ ).‎ 因为f(x)在上是增函数，‎ 所以⊆.‎ 所以－≥－且≤，所以ω∈.‎ 法二　因为x∈，ω>0.‎ 所以ωx∈，‎ 又f(x)在区间上是增函数，‎ 所以⊆，‎ 则又ω>0，‎ 得0<ω≤.‎ 法三　因为f(x)在区间上是增函数，故原点到－，的距离不超过，即得T≥，即≥，又ω>0，得0<ω≤.‎ 答案　(1)(k∈ )　(2) 规律方法　(1)求较为复杂的三角函数的单调区间时，首先化简成y＝Asin(ωx＋φ)形式，再求y＝Asin(ωx＋φ)的单调区间，只需把ωx＋φ看作一个整体代入y＝sin x的相应单调区间内即可，注意要先把ω化为正数.(2)对于已知函数的单调区间的某一部分确定参数ω的范围的问题，首先，明确已知的单调区间应为函数的单调区间的子集，其次，要确定已知函数的单调区间，从而利用它们之间的关系可求解.‎ ‎【训练2】 (1)函数f(x)＝tan的单调递增区间是________.‎ ‎(2)已知ω>0，函数f(x)＝sin在上单调递减，则ω的取值范围是________.‎ 解析　(1)由kπ－<2x－0，得 ＋<ωx＋<ωπ＋，‎ 又y＝sin x的单调递减区间为，k∈ ，‎ 所以 解得4k＋≤ω≤2k＋，k∈ .‎ 又由4k＋－≤0，k∈ 且2k＋>0，k∈ ，‎ 得k＝0，所以ω∈.‎ 答案　(1)(k∈ )　(2) 考点三　三角函数的奇偶性与对称性(多维探究)‎ 命题角度1　奇偶性 ‎【例3－1】 (1)(2017·常州期末)函数y＝2cos2－1是最小正周期为________的________函数(填“奇”或“偶”).‎ ‎(2)(2018·衡水中 金卷)设函数f(x)＝sin－cos的图象关于y轴对称，则θ＝________.‎ 解析　(1)y＝2cos2－1‎ ‎＝cos2＝cos＝cos＝sin 2x，‎ 则函数为最小正周期为π的奇函数.‎ ‎(2)f(x)＝sin－cos＝‎ ‎2sin，由题意可得f(0)＝2sin＝±2，即sin＝±1，∴θ－＝＋kπ(k∈ )，∴θ＝＋kπ(k∈ )，∵|θ|<，∴k＝－1时，θ＝－.‎ 答案　(1)π　奇　(2)－ 命题角度2　轴对称 ‎【例3－2】 (1)(2017·苏、锡、常、镇四市调研)若函数f(x)＝2sin(4x＋φ)(φ<0)的图象关于直线x＝对称，则φ的最大值为________.‎ ‎(2)(2016·全国Ⅰ卷改编)已知函数f(x)＝sin(ωx＋φ)，x＝－为f(x)的零点，x＝为y＝f(x)图象的对称轴，且f(x)在上单调，则ω的最大值为________.‎ 解析　(1)由题可得，4×＋φ＝＋kπ，k∈ ，∴＝＋kπ，k∈ ，∵φ<0，∴φmax＝－.‎ ‎(2)因为x＝－为f(x)的零点，x＝为f(x)的图象的对称轴，－＝＋，即＝＝·，解得ω＝2k＋1(k∈N)，又因为f(x)在上单调，所以－＝≤＝，即ω≤12，令ω＝11，∵x＝是y＝f(x)的对称轴，∴＋φ＝＋kπ(k∈N).又由|φ|≤，解得φ＝－，此时f(x)＝sin，f(x)在上递增，在上递减，不满足f(x)在上单调；同理令ω＝9，则φ＝，此时f(x)＝sin，满足f(x)在上单减，综上，ω的最大值为9.‎ 答案　(1)－　(2)9‎ 命题角度3　中心对称 ‎【例3－3】 (1)已知函数y＝2sin的图象关于点P(x0，0)对称，若x0∈，则x0＝________.‎ ‎(2)若函数y＝cos(ω∈N*)图象的一个对称中心是，则ω的最小值为________.‎ 解析　(1)由题意可知2x0＋＝kπ，k∈ ，‎ 故x0＝－，k∈ ，‎ 又x0∈，∴－≤k≤，k∈ ，‎ ‎∴k＝0，则x0＝－.‎ ‎(2)由题意知π＋＝kπ＋(k∈ )，‎ ‎∴ω＝6k＋2(k∈ )，又ω∈N*，∴ωmin＝2.‎ 答案　(1)－　(2)2‎ 规律方法　(1)若f(x)＝Asin(ωx＋φ)(A，ω≠0)，则 ② f(x)为偶函数的充要条件是φ＝＋kπ(k∈ )；‎ ‎②f(x)为奇函数的充要条件是φ＝kπ(k∈ ).‎ ‎(2)对于可化为f(x)＝Asin(ωx＋φ)形式的函数，如果求f(x)的对称轴，只需令ωx＋φ＝＋kπ(k∈ )，求x即可；如果求f(x)的对称中心的横坐标，只需令ωx＋φ＝kπ(k∈ )，求x即可.‎ ‎(3)对于可化为f(x)＝Acos(ωx＋φ)形式的函数，如果求f(x)的对称轴，只需令ωx＋φ＝kπ(k∈ )，求x即可；如果求f(x)的对称中心的横坐标，只需令ωx＋φ＝＋kπ(k∈ )，求x即可.‎ ‎【训练3】 (1)(2017·无锡期末)若函数f(x)＝cos的图象关于点(x0，0‎ ‎)成中心对称，x0∈，则x0＝______.‎ ‎(2)(2018·盐城模拟)当x＝时，函数f(x)＝sin(x＋φ)取得最小值，则下列关于函数y＝f的说法正确的是________(填序号).‎ ‎①是奇函数且图象关于点对称；‎ ‎②是偶函数且图象关于点(π，0)对称；‎ ‎③且奇函数且图象关于直线x＝对称；‎ ‎④是偶函数且图象关于直线x＝π对称.‎ 解析　(1)因为f(x)＝cos＝cos＝－sin 2x，由2x0＝kπ，k∈ 得x0＝，k∈ .‎ 由x0∈，故k＝0，1时，x0＝0，.‎ ‎(2)∵当x＝时，函数f(x)取得最小值，‎ ‎∴sin＝－1，∴φ＝2kπ－(k∈ )，‎ ‎∴f(x)＝sin＝sin，‎ ‎∴y＝f ＝sin(－x)＝－sin x，‎ ‎∴y＝f 是奇函数，且图象关于直线x＝对称.‎ 答案　(1)0或　(2)③‎ 一、必做题 ‎1.(2017·江苏押题卷)已知函数f(x)＝2sin(ω>0)的最小正周期为T＝π，则ω＝________.‎ 解析　因为T＝，所以＝π，故ω＝3.‎ 答案　3‎ ‎2.(2017·南京模拟)若函数f(x)＝sin(ω>0)的最小正周期为π，则f的值是________.‎ 解析　由题意得＝π，所以ω＝2，f(x)＝sin.因此f＝sin＝sin ＝.‎ 答案　 ‎3.(2018·南京模拟)函数f(x)＝tan的单调递增区间是________.‎ 解析　当kπ－＜2x－＜kπ＋(k∈ )时，函数y＝tan单调递增，解得－＜x＜＋(k∈ )，所以函数y＝tan的单调递增区间是(k∈ ).‎ 答案　(k∈ )‎ ‎4.(2018·南通、扬州、泰州、淮安调研)设函数y＝sin(00，且·ω≤π.所以0<ω≤.当x＝时，2cosπ＝1，cosπ＝.‎ 所以ω＝.‎ 答案　 ‎12.(2018·南通调研)已知函数f(x)＝a＋b.‎ ‎(1)若a＝－1，求函数f(x)的单调增区间；‎ ‎(2)若x∈[0，π]时，函数f(x)的值域是[5，8]，求a，b的值.‎ 解　f(x)＝a(1＋cos x＋sin x)＋b＝asin＋a＋b.‎ ‎(1)当a＝－1时，f(x)＝－sin＋b－1，‎ 由2kπ＋≤x＋≤2kπ＋(k∈ )，‎ 得2kπ＋≤x≤2kπ＋(k∈ )，‎ ‎∴f(x)的单调增区间为(k∈ ).‎ ‎(2)∵0≤x≤π，∴≤x＋≤，‎ ‎∴－≤sin≤1，依题意知a≠0.‎ ‎(ⅰ)当a>0时，∴a＝3－3，b＝5.‎ ‎(ⅱ)当a<0时，∴a＝3－3，b＝8.‎ 综上所述，a＝3－3，b＝5或a＝3－3，b＝8‎