【数学】2018届一轮复习苏教版函数教案 3页

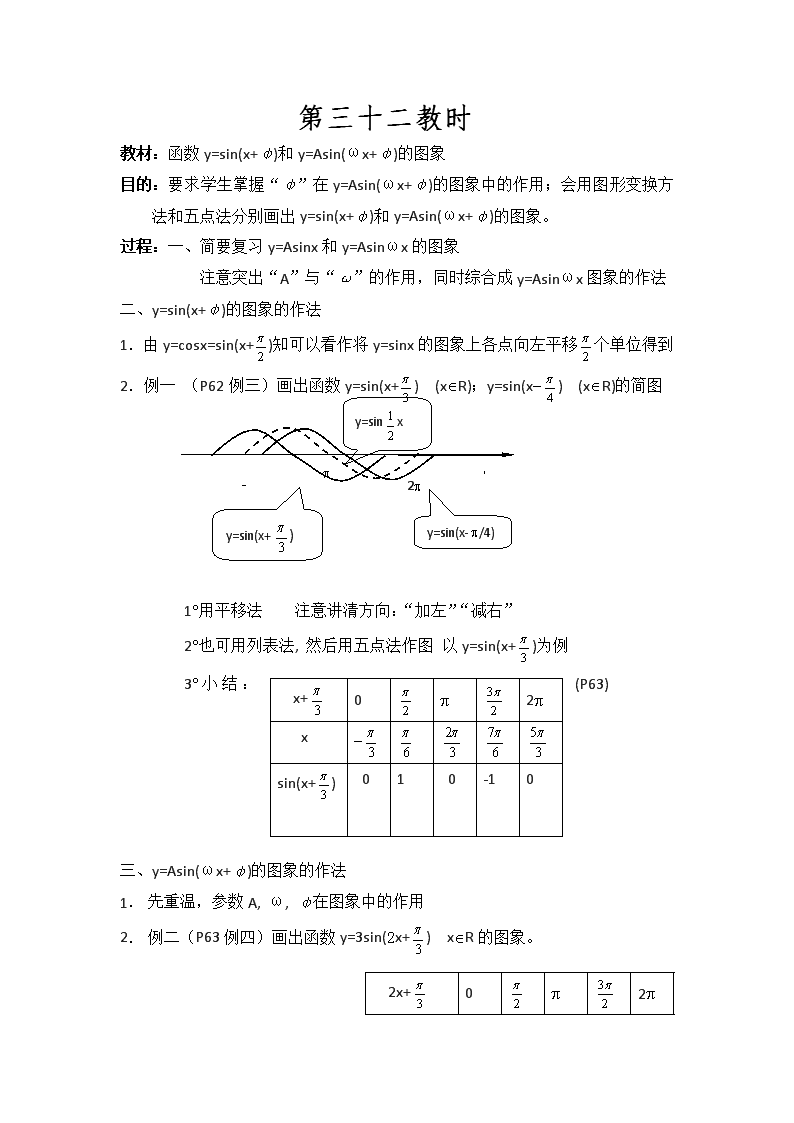
第三十二教时 教材：函数y=sin(x+φ)和y=Asin(ωx+φ)的图象 目的：要求学生掌握“φ”在y=Asin(ωx+φ)的图象中的作用；会用图形变换方法和五点法分别画出y=sin(x+φ)和y=Asin(ωx+φ)的图象。‎ 过程：一、简要复习y=Asinx和y=Asinωx的图象 注意突出“A”与“ω”的作用，同时综合成y=Asinωx图象的作法 二、y=sin(x+φ)的图象的作法 ‎1．由y=cosx=sin(x+)知可以看作将y=sinx的图象上各点向左平移个单位得到 y=sinx y ‎2．例一 （P62例三）画出函数y=sin(x+) (xÎR)；y=sin(x-) (xÎR)的简图 ‎1‎ p ‎4p ‎3p ‎2p -1‎ p O x y=sin(x-p/4)‎ y=sin(x+)‎ ‎1°用平移法 注意讲清方向：“加左”“减右”‎ ‎2°也可用列表法, 然后用五点法作图 以y=sin(x+)为例 x+‎ ‎0‎ p ‎2p ‎ x - sin(x+)[来源:Z,xx,k.Com]‎ ‎ 0‎ ‎1‎ ‎ 0‎ ‎-1‎ ‎0‎ ‎3°小结：(P63)‎ ‎ http://wx.jtyjy.com/‎ 三、y=Asin(ωx+φ)的图象的作法 1． 先重温，参数A, ω, φ在图象中的作用 2． 例二（P63例四）画出函数y=3sin(2x+) xÎR的图象。‎ ‎2x+‎ ‎0‎ p ‎2p ‎ x - ‎3sin(2x+)‎ ‎ 0‎ ‎3‎ ‎ 0‎ ‎-3‎ ‎0‎ 解：周期T=p（五点法）‎ 令X=2x+则x=‎ y=sin(2x+)‎ y=sin(x+)‎ ‎1‎ y p ‎4p ‎3p p O x -1‎ 1． 用平移法作y=3sin(2x+)的图象 2． 小结平移法过程（步骤）P64-65略 作y=sinx（长度为2p的某闭区间）‎ 得y=sin(x+φ)‎ 得y=sinωx 得y=sin(ωx+φ)‎ 得y=sin(ωx+φ)‎ 得y=Asin(ωx+φ)的图象，先在一个周期闭区间上再扩充到R上。‎ 沿x轴平 移|φ|个单位 横坐标 伸长或缩短 横坐标伸 长或缩短 沿x轴平 移||个单位 纵坐标伸 长或缩短 纵坐标伸 长或缩短 ‎[来源: http://wx.jtyjy.com/]‎ 两种方法殊途同归 四、小结：1．突出A, ω, φ的作用[来源:金太阳新课标资源网]‎ ‎2．强调y=Asin(ωx+φ)图象的平移步骤及五点法 五、作业：P8习题4.9 2中 ③④ 及3‎ ‎ ‎ ‎ ‎