【数学】2018届一轮复习北师大版第十章计数原理概率随机变量及其分布第一节两个计数原理教案 11页

第一节　两个计数原理 ‎☆☆☆2017考纲考题考情☆☆☆‎ 考纲要求 真题举例 命题角度 ‎1.理解分类加法计数原理和分步乘法计数原理，能正确区分“类”和“步”； ‎ ‎2.能利用两个原理解决一些简单的实际问题。‎ ‎2016，全国卷Ⅱ，5,5分(乘法计数原理)‎ ‎2016，全国卷Ⅲ，12,5分(加法计数原理)‎ ‎2014，福建卷，10,5分(乘法计数原理)‎ ‎　　1.两个计数原理一般不单独命题，常与排列、组合交汇考查；‎ ‎2.题型以选择题、填空题为主，要求相对较低。‎ 微知识　小题练 自|主|排|查 两个计数原理：‎ 完成一件事的策略 完成这件事共有的方法 分类加法计数原理 有n类不同方案，在第1类方案中有m1种不同的方法，在第2类方案中有m2种不同的方法…在n类中有mn种不同方法 N＝m1＋m2＋…＋mn种不同的方法 分步乘法计数原理 需要n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法…做第n步有mn种不同方法 N＝m1·m2·…·mn种不同的方法 微点提醒 ‎1．分类加法计数原理与分类有关，各种方法相互独立，用其中的任意一种方法都可以完成这件事。‎ ‎2．分步乘法计数原理与分步有关，各个步骤相互依存，只有各个步骤都完成了，这件事才能完成。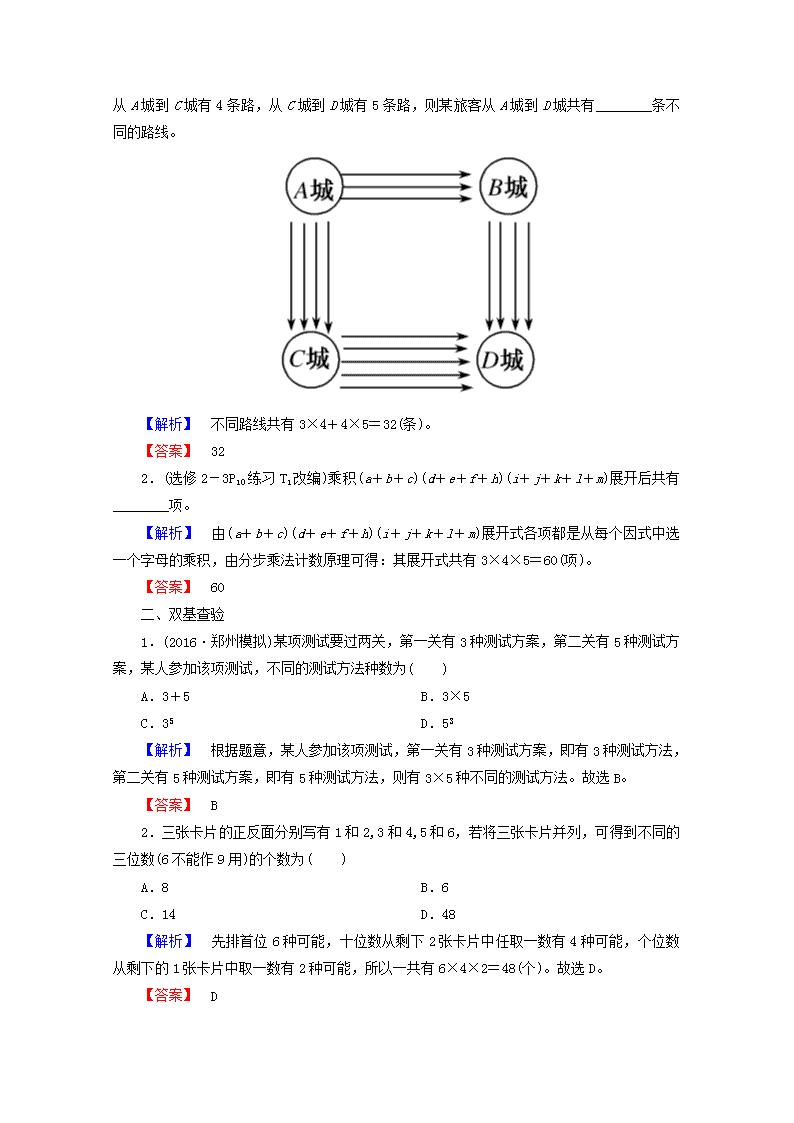‎ 小|题|快|练 一 、走进教材 ‎1．(选修2－3P‎12A组T2改编)如图，从A城到B城有3条路；从B城到D 城有4条路；从A城到C城有4条路，从C城到D城有5条路，则某旅客从A城到D城共有________条不同的路线。‎ ‎【解析】　不同路线共有3×4＋4×5＝32(条)。‎ ‎【答案】　32‎ ‎2．(选修2－3P10练习T1改编)乘积(a＋b＋c)(d＋e＋f＋h)(i＋j＋k＋l＋m)展开后共有________项。‎ ‎【解析】　由(a＋b＋c)(d＋e＋f＋h)(i＋j＋k＋l＋m)展开式各项都是从每个因式中选一个字母的乘积，由分步乘法计数原理可得：其展开式共有3×4×5＝60(项)。‎ ‎【答案】　60‎ 二、双基查验 ‎1．(2016·郑州模拟)某项测试要过两关，第一关有3种测试方案，第二关有5种测试方案，某人参加该项测试，不同的测试方法种数为(　　)‎ A．3＋5 B．3×5‎ C．35 D．53‎ ‎【解析】　根据题意，某人参加该项测试，第一关有3种测试方案，即有3种测试方法，第二关有5种测试方案，即有5种测试方法，则有3×5种不同的测试方法。故选B。‎ ‎【答案】　B ‎2．三张卡片的正反面分别写有1和2,3和4,5和6，若将三张卡片并列，可得到不同的三位数(6不能作9用)的个数为(　　)‎ A．8 B．6‎ C．14 D．48‎ ‎【解析】　先排首位6种可能，十位数从剩下2张卡片中任取一数有4种可能，个位数从剩下的1张卡片中取一数有2种可能，所以一共有6×4×2＝48(个)。故选D。‎ ‎【答案】　D ‎3．已知两条异面直线a，b上分别有5个点和8个点，则这13个点可以确定不同的平面个数为(　　)‎ A．40 B．16‎ C．13 D．10‎ ‎【解析】　分两类情况讨论：‎ 第1类，直线a分别与直线b上的8个点可以确定8个不同的平面；第2类，直线b分别与直线a上的5个点可以确定5个不同的平面。根据分类加法计数原理知，共可以确定8＋5＝13个不同的平面。故选C。‎ ‎【答案】　C ‎4．(2017·洛阳模拟)某位同学逛书店，发现有三本喜欢的书，决定至少买其中一本，则购买的方案有________种。‎ ‎【解析】　至少买其中一本的实质是买一本或买两本或买三本，故分三类完成。第一类：买一本有3种；第二类：买两本有3种；第三类：买三本有1种。共有3＋3＋1＝7(种)买法。‎ ‎【答案】　7‎ ‎5．(2016·广州模拟)在三位正整数中，若十位数字小于个位和百位数字，则称该数为“驼峰数”。比如“‎102”‎，“‎546”‎为“驼峰数”，由数字1,2,3,4可构成无重复数字的“驼峰数”有________个。‎ ‎【解析】　十位上的数为1时，有213,214,312,314,412,413，共6个，十位上的数为2时，有324,423，共2个，所以共有6＋2＝8(个)。‎ ‎【答案】　8‎ 微考点　大课堂 考点一 ‎ 分类加法计数原理 ‎【典例1】　(1)(2016·太原模拟)在所有的两位数中，个位数字大于十位数字的两位数的个数为________。‎ ‎(2)我们把各位数字之和为6的四位数称为“六合数”(如2 013是“六合数”)，则首位为2的“六合数”共有(　　)‎ A．18个　　B．15个　　C．12个　　D．9个 ‎【解析】　(1)根据题意，将十位上的数字按1,2,3,4,5,6,7,8的情况分成8类，在每一类中满足题目条件的两位数分别是8个，7个，6个，5个，4个，3个，2个，1个。‎ 由分类加法计数原理知，符合条件的两位数共有8＋7＋6＋5＋4＋3＋2＋1＝36(个)。‎ 故共有36个。‎ ‎(2)设满足题意的“六合数”为2 000＋‎100a＋10b＋c，则a＋b＋c＝4，满足条件的a，‎ b，c可分以下四种情况：(1)一个为4，两个为0，共有3个；(2)一个为3，一个为1，一个为0，共有6个；(3)两个为2，一个为0，共有3个；(4)一个为2，两个为1，共有3个。则首位为2的“六合数”共有15个。故选B。‎ ‎【答案】　(1)36　(2)B 反思归纳　使用分类加法计数原理遵循的原则 有时分类的划分标准有多个，但不论是以哪一个为标准，都应遵循“标准要明确，不重不漏”的原则。‎ ‎【变式训练】　从集合{1,2,3，…，10}中任意选出三个不同的数，使这三个数成等比数列，这样的等比数列的个数为(　　)‎ A．3 B．4 ‎ C．6 D．8‎ ‎【解析】　当公比为2时，等比数列可为1,2,4或2,4,8；当公比为3时，等比数列可为1,3,9；当公比为时，等比数列可为4,6,9。故选D。‎ ‎【答案】　D 考点二 ‎ 分步乘法计数原理 ‎【典例2】　(1)(2016·全国卷Ⅱ)如图，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为(　　)‎ A．24 B．18 ‎ C．12 D．9‎ ‎(2)(2016·四川高考)用数字1,2,3,4,5组成没有重复数字的五位数，其中奇数的个数为(　　)‎ A．24 B．48 ‎ C．60 D．72‎ ‎【解析】　(1)由题意可知E→F共有6种走法，F→G 共有3种走法，由乘法计数原理知，共有6×3＝18种走法，故选B。‎ ‎(2)由题意，可知个位可以从1,3,5中任选一个，有A种方法，其他数位上的数可以从剩下的4个数字中任选，进行全排列，有A种方法，所以奇数的个数为AA＝3×4×3×2×1＝72，故选D。‎ ‎【答案】　(1)B　(2)D 反思归纳　分步乘法计数原理的注意点 ‎1．明确题目中所指的“完成一件事”是什么事，必须要经过几步才能完成这件事。‎ ‎2．解决分步问题时要合理设计步骤、顺序，使各步互不干扰，还要注意元素是否可以重复选取。‎ ‎【变式训练】　(1)(2016·锦州模拟)5名应届毕业生报考三所高校，每人报且仅报一所院校，则不同的报名方法的种数是(　　)‎ A．35 B．53 ‎ C．A D．C ‎(2)(2016·哈尔滨模拟)用0,1，…，9十个数字，可以组成有重复数字的三位数的个数为(　　)‎ A．243 B．252 ‎ C．261 D．279‎ ‎(3)设集合A＝{－1,0,1}，集合B＝{0,1,2,3}，定义A*B＝{(x，y)|x∈A∩B，y∈A∪B}，则A*B中元素的个数是(　　)‎ A．7 B．10 ‎ C．25 D．52‎ ‎【解析】　(1)根据分步乘法计数原理知，每个学生都有3个可能报名的学校，故应该是3×3×3×3×3＝35(种)方法。故选A。‎ ‎(2)由分步乘法计数原理得，能够组成的三位数的个数是9×10×10＝900，能够组成无重复数字的三位数的个数是9×9×8＝648，故能够组成有重复数字的三位数的个数是900－648＝252。故选B。‎ ‎(3)由题意知本题是一个分步乘法计数原理，因为集合A＝{－1,0,1}，集合B＝{0,1,2,3}，所以A∩B＝{0,1}，A∪B＝{－1,0,1,2,3}，所以x有2种取法，y有5种取法，所以根据分步乘法计数原理得2×5＝10。故选B。‎ ‎【答案】　(1)A　(2)B　(3)B 考点三 ‎ 两个计数原理的综合应用多维探究 角度一：排数与排队问题 ‎【典例3】　(1)(2015·四川高考)用数字0,1,2,3,4,5组成没有重复数字的五位数，其中比40 000大的偶数共有(　　)‎ A．144个 B．120个 ‎ C．96个 D．72个 ‎(2)(2017·长春模拟)现从甲、乙、丙等6名工人中安排4人分别照看一道工序，第一道工序只能从甲、乙两工人中安排1人，第四道工序只能从甲、丙两工人中安排1人，则不同的安排方案共有(　　)‎ A．24种 B．36种 ‎ C．48种 D．72种 ‎【解析】　(1)①首位为5，末位为0：4×3×2＝24(个)；‎ ‎②首位为5，末位为2：4×3×2＝24(个)；‎ ‎③首位为5，末位为4：4×3×2＝24(个)；‎ ‎④首位为4，末位为0：4×3×2＝24(个)；‎ ‎⑤首位为4，末位为2：4×3×2＝24(个)。‎ 由分类加法计数原理，得共有24＋24＋24＋24＋24＝120(个)。故选B。‎ ‎(2)分两类：‎ ‎①第一道工序安排甲时有1×1×4×3＝12(种)。‎ ‎②第一道工序不安排甲时有1×2×4×3＝24(种)。‎ 所以共有12＋24＝36(种)。故选B。‎ ‎【答案】　(1)B　(2)B 角度二：涂色问题 ‎【典例4】　(2016·珠海模拟)如图，用6种不同的颜色把图中A，B，C，D四块区域分开，若相邻区域不能涂同一种颜色，则不同的涂法共有(　　)‎ A．400种 B．460种 ‎ C．480种 D．496种 ‎【解析】　完成此事可能使用4种颜色，也可能使用3种颜色。当使用4种颜色时：从A开始，有6种方法，B有5种，C有4种，D有3种，完成此事共有6×5×4×3＝360(种)方法；当使用3种颜色时：A，D使用同一种颜色，从A，D开始，有6种方法，B有5种，C 有4种，完成此事共有6×5×4＝120(种)方法。由分类加法计数原理可知：不同涂法有360＋120＝480(种)。故选C。‎ ‎【答案】　C 反思归纳　1.(1)注意在综合应用两个原理解决问题时，一般是先分类再分步。在分步时可能又用到分类加法计数原理。(2)注意对于较复杂的两个原理综合应用的问题，可恰当地列出示意图或列出表格，使问题形象化、直观化。‎ ‎2．解决涂色问题，可按颜色的种数分类，也可按不同的区域分步完成。‎ 微考场　新提升 ‎1．(2016·滨州模拟)甲、乙两人从4门课程中各选修2门，则甲、乙所选的课程中恰有1门相同的选法有(　　)‎ A．6种　　　　　　　　 B．12种 C．24种 D．30种 解析　可分步完成此事：‎ 第一步：甲乙选相同的1门共有4种方法；第二步：甲再选1门有3种方法；第三步：乙再选一门有2种选法，由分步乘法计数原理知：甲、乙所选的课程中恰有1门相同的选法有4×3×2＝24(种)。故选C。‎ 答案　C ‎2．(2017·成都模拟)某城市有3个演习点同时进行消防演习，现将4名消防队分配到这3个演习点，若每个演习点至少安排1名消防队，则不同的分配方案种数为(　　)‎ A．12 B．36‎ C．72 D．108‎ 解析　先从4个消防队中选出2个作为一个整体，有C种选法；再将三个整体进行全排列，有A种方法；根据分步乘法计数原理得不同的分配方案种数为C·A＝36。故选B。‎ 答案　B ‎3．(2016·银川模拟)集合P＝{x,1}，Q＝{y,1,2}，其中x，y∈{1,2,3，…，9}，且P⊆Q。把满足上述条件的一个有序整数对(x，y)作为一个点的坐标，则这样的点的个数是(　　)‎ A．9 B．14‎ C．15 D．21‎ 解析　当x＝2时，x≠y，点的个数为1×7＝7(个)；当x≠2时，x＝y，点的个数为7×1＝7(个)，则共有14个点。故选B。‎ 答案　B ‎4．(2016·长春模拟)直线Ax＋By＝0，若从集合E＝{0,1,3,5,7,8}中每次取出两个不同的数作为A，B的值，则可表示________条不同的直线。‎ 解析　若A或B中有一个为零时，有2条；若AB≠0时，有5×4＝20条，由分类加法计数原理可知：共有2＋20＝22条不同的直线。‎ 答案　22‎ ‎5．(2016·郑州模拟)用数字2,3组成四位数，且数字2,3至少都出现一次，这样的四位数共有________个。(用数字作答)‎ 解析　数字2,3至少都出现一次，包括以下情况：‎ ‎“‎2”‎出现1次，共有4种方法，“‎3”‎出现3次，共有1种方法，共可组成4×1＝4(个)四位数。‎ ‎“‎2”‎出现2次，共有C＝6种方法，“‎3”‎出现2次，共有1种方法，共可组成6×1＝6(个)四位数。‎ ‎“‎2”‎出现3次，共有C＝4种方法，“‎3”‎出现1次，共有1种方法，共可组成4×1＝4(个)四位数。‎ 综上所述，共可组成4＋6＋4＝14个四位数。‎ 答案　14‎ 微专题　巧突破 利用两个计数原理解决的两大题型 ‎1．几何问题 将两个基本计数原理与立体几何知识结合起来考查，既考查了同学们的逻辑推理能力，又考查了同学们的空间想象能力，具有较强的综合性。‎ ‎【典例1】　　如果一条直线与一个平面垂直，那么称此直线与平面构成一个“正交线面对”。在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是(　　)‎ A．48 B．18‎ C．24 D．36‎ ‎【思路分析】　‎ ‎【解析】　分情况讨论：‎ 第1类，对于每一条棱，都可以与两个侧面构成“正交线面对”，这样的“正交线面对”有2×12＝24(个)；‎ 第2类，对于每一条面对角线，都可以与一个对角面构成“正交线面对”，这样的“正交线面对”有12个。‎ 所以正方体中“正交线面对”共有24＋12＝36(个)。‎ ‎【答案】　D ‎【变式训练1】　从正方体六个面的对角线中任取两条作为一对，其中所成的角为60°的共有(　　)‎ A．24对 B．30对 C．48对 D．60对 ‎【解析】　正方体中共有12条面对角线，任取两条作为一对共有C＝66对，12条对角线中的两条所构成的关系有平行、垂直、成60°角。相对两面上的4条对角线组成的C＝6对组合中，平行有2对，垂直有4对，所以所有的平行和垂直共有‎3C＝18对。所以成60°角的有C－‎3C＝66－18＝48(对)。故选C。‎ ‎【答案】　C ‎2．集合问题 解决集合问题时，常以有特殊要求的集合为标准进行分类，常用的结论有{a1，a2，a3，…，an}的子集有2n个，真子集有2n－1个。‎ ‎【典例2】　　设集合I＝{1,2,3,4,5}，选择I的两个非空子集A和B，要使B 中最小的数大于A中最大的数，则不同的选择方法共有(　　)‎ A．50种 B．49种 C．48种 D．47种 ‎【思路分析】　‎ ‎【解析】　根据题意，B中最小的数大于A中最大的数，则集合A，B中没有相同的元素，且都不是空集。按A中元素分情况讨论，分别计算其选法种数，进而相加即可。‎ 第1类，当A中最大的数是1时，A是{1}，B可以是{2,3,4,5}的非空子集，即有24－1＝15(种)选法；‎ 第2类，当A中最大的数是2时，A可以是{2}或{1,2}，B可以是{3,4,5}的非空子集，即有2×(23－1)＝14(种)选法；‎ 第3类，当A中最大的数是3时，A可以是{3}，{1,3}，{2,3}，{1,2,3}，B可以是{4,5}的非空子集，即有4×(22－1)＝12(种)选法；‎ 第4类，当A中最大的数是4时，A可以是{4}，{1,4}，{2,4}，{3,4}，{1,2,4}，{1,3,4}，{2,3,4}，{1,2,3,4}，B是{5}，即有8×1＝8(种)选法。‎ 综上可知，共有15＋14＋12＋8＝49(种)不同的选择方法。‎ ‎【答案】　B ‎【方法探究】　本题也可以按如下方法求解：集合A，B中没有相同的元素，且都不是空集，也就是要求至少从集合I中选取2个元素才能构造出满足要求的集合，因此只要从集合I中选出元素，把这些元素按照从小到大排列后，将其分为两部分即可。‎ ‎【变式训练2】　(2016·衡水调研)设集合S＝{1,2,3,4,5,6,7,8,9}，集合A＝{a1，a2，a3}，A⊆S，a1，a2，a3满足a1