四川省蓉城名校联盟2020-2021学年高二(高中2019级)第一学期期中联考理科数学试卷 8页

蓉城名校联盟2020～2021学年度上期高中2019级期中联考 理科数学 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．若直线a⊥平面α，直线b⊥平面α，则直线a与直线b的位置关系为 A．异面 B．相交 C．平行 D．平行或异面 ‎2．已知直线l经过点A（1，-1），B（2，m），若直线l的斜率为1，则m的值为 A．0 B．1 C．-1 D．2‎ ‎3．某校高一、高二、高三共有2800名学生，为了解暑假学生在家的每天学习情况，计划用分层抽样的方法抽取一个容量为56人的样本，已知从高二学生中抽取的人数为19人，则该校高二学生人数为 A．900 B．950 C．1000 D．1050‎ ‎4．已知点A（1，0），直线l：x-y＋1＝0，则点A到直线l的距离为 A．1 B．2 C． D．‎ ‎5．若直线2x-y＋a＝0始终平分圆x2＋y2-4x＋4y＝0的周长，则a的值为 A．4 B．6 C．-6 D．-2‎ ‎6．设α、β是互不重合的平面，l、m、n是互不重合的直线，下列命题正确的是 A．若mα，nα，l⊥m，，l⊥n，则l⊥α B．若l⊥n，m⊥n，则l∥m C．若m∥α，n∥β，α⊥β，则m⊥n D．若l⊥α，l∥β，则α⊥β ‎7．若实数x，y满足约束条件，则z＝3x-y的最小值为 A．-6 B．-5 C．-4 D．-2‎ ‎8．如图，在以下四个正方体中，直线MN与平面ABC平行的是 A． B．‎ C． D．‎ ‎9．直线2y-x＋1＝0关于y-x＋3＝0对称的直线方程是 A．2x-y-8＝0 B．2x-y-10＝0 C．2x＋y-12＝0 D．2x＋y-10＝0‎ ‎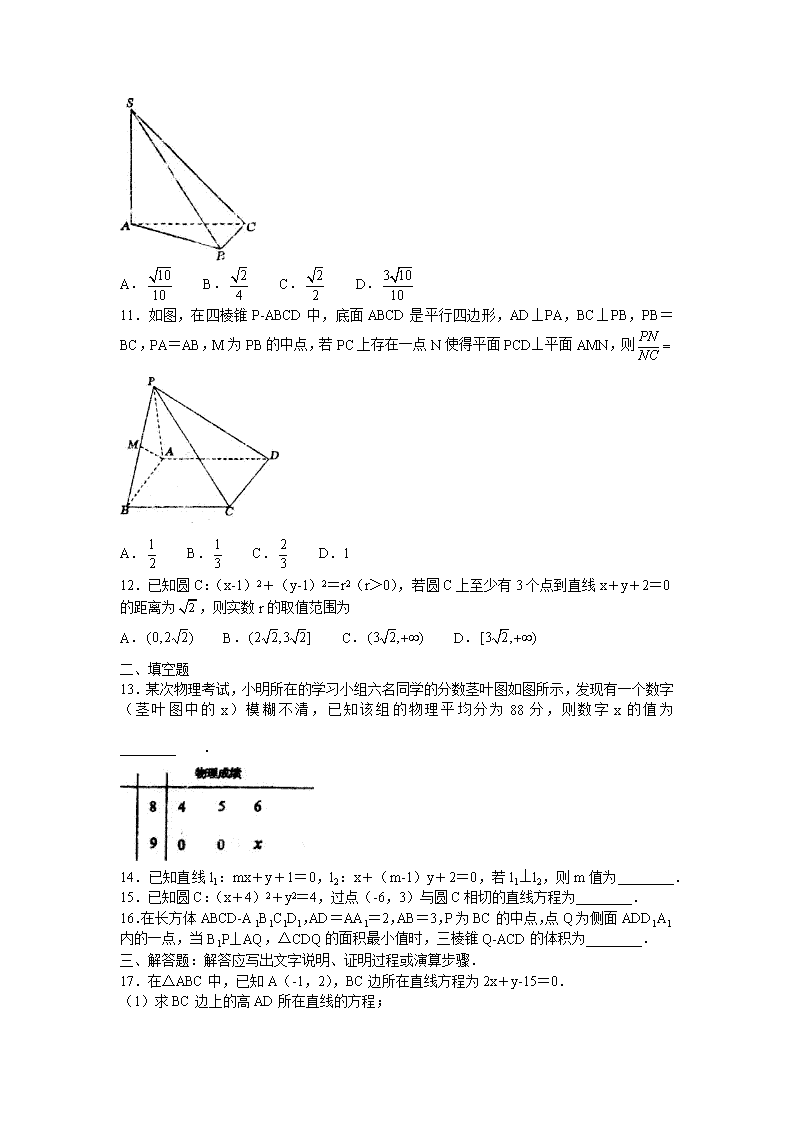10．如图，在三棱锥S-ABC中，SA⊥平面ABC，SA＝2，AC＝2．BC＝1，∠ACB＝90°，则直线SC与平面SAB所成角的正弦值为 A． B． C． D．‎ ‎11．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，AD⊥PA，BC⊥PB，PB＝BC，PA＝AB，M为PB的中点，若PC上存在一点N使得平面PCD⊥平面AMN，则 A． B． C． D．1‎ ‎12．已知圆C：（x-1）2＋（y-1）2＝r2（r＞0），若圆C上至少有3个点到直线x＋y＋2＝0的距离为，则实数r的取值范围为 A． B． C． D．‎ 二、填空题 ‎13．某次物理考试，小明所在的学习小组六名同学的分数茎叶图如图所示，发现有一个数字（茎叶图中的x）模糊不清，已知该组的物理平均分为88分，则数字x的值为________．‎ ‎14．已知直线l1：mx＋y＋1＝0，l2：x＋（m-1）y＋2＝0，若l1⊥l2，则m值为________．‎ ‎15．已知圆C：（x＋4）2＋y2＝4，过点（-6，3）与圆C相切的直线方程为________．‎ ‎16．在长方体ABCD-A1B1C1D1，AD＝AA1＝2，AB＝3，P为BC的中点，点Q为侧面ADD1A1内的一点，当B1P⊥AQ，△CDQ的面积最小值时，三棱锥Q-ACD的体积为________．‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17．在△ABC中，已知A（-1，2），BC边所在直线方程为2x＋y-15＝0．‎ ‎（1）求BC边上的高AD所在直线的方程；‎ ‎（2）若AB，AC边的中点分别为E，F，求直线EF的方程．‎ ‎18．已知圆C经过点A（1，0）和B（-1，-2），且圆心C在直线3x-4y-11＝0上．‎ ‎（1）求圆C的方程；‎ ‎（2）若圆C与圆M：x2＋y2＋4x-2ay＋a2-5＝0相交，求实数a的取值范围．‎ ‎19．如图，四面体ABCD中，点E，F分别为线段AC，AD的中点，平面EFNM∩平面BCD＝MN，∠CDA＝∠CDB＝90°，DH⊥AB，垂足为H．‎ ‎（1）求证：EF∥MN；‎ ‎（2）求证：平面CDH⊥平面ABC．‎ ‎20．成都是全国闻名的旅游城市，有许多很有特色的旅游景区．某景区为了提升服务品质，对过去100天每天的游客数进行了统计分析，发现这100天每天的游客数都没有超出八千人，统计结果见下面的频率分布直方图：‎ ‎（1）估计该景区每天游客数的中位数和平均数；‎ ‎（2）为了研究每天的游客数是否和当天的最高气温有关，从这一百天中随机抽取了5天，统计出这5天的游客数（千人）分别为0.8、3.7、5.1、5.6、6.8，已知这5天的最高气温（℃）依次为8、18、22、24、28．‎ ‎（ⅰ）根据以上数据，求游客数y关于当天最高气温x的线性回归方程（系数保留一位小数）；‎ ‎（ⅱ）根据（ⅰ）中的回归方程，估计该景区这100天中最高气温在20 ℃～26 ℃内的天数（保留整数）．‎ 参考公式：由最小二乘法所得回归直线的方程是；其中，‎ ‎，．本题参考数据：‎ ‎，．‎ ‎21．如图，六面体ABCDEFGH中，平面ABCD∥平面EFGH，EF＝2AB．‎ ‎（1）若AE⊥EF，平面ABFE⊥平面EFGH，二面角F-AE-H的大小为120°，AB＝AE＝1，EH＝2，求三棱锥A-EFH的体积；‎ ‎（2）若A，E，G，C四点共面，求证：直线FB与HD相交．‎ ‎22．已知圆C：（x＋3）2＋（y-4）2＝16，直线l：（2m＋1）x＋（m-2）y-3m-4＝0（m∈R）．‎ ‎（1）若圆C截直线l所得弦AB的长为，求m的值；‎ ‎（2）若m＞0，直线l与圆C相离，在直线l上有一动点P，过P作圆C的两条切线PM，PN，切点分别为M，N，且cos∠MPN的最小值为．求m的值，并证明直线MN经过定点．‎