【数学】2018届一轮复习北师大版第四章平面向量数系的扩充与复数的引入第一节平面向量的概念及其线性运算教案 10页

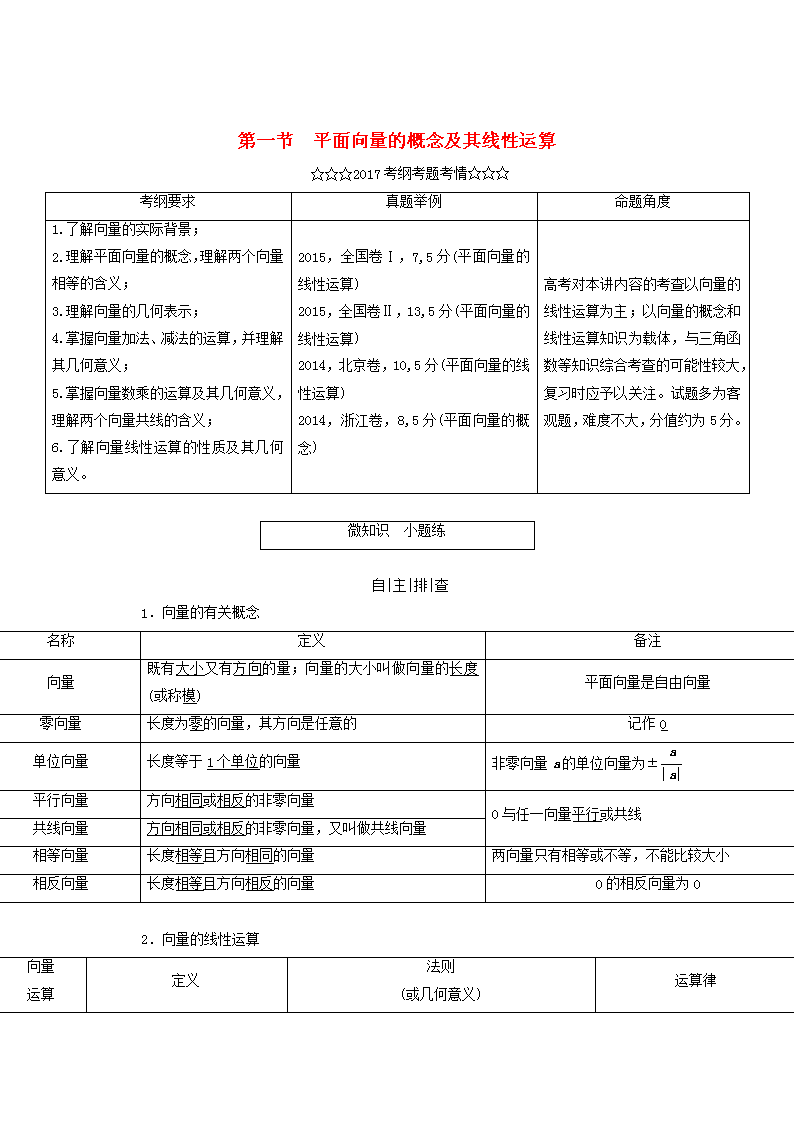
第一节　平面向量的概念及其线性运算 ‎☆☆☆2017考纲考题考情☆☆☆‎ 考纲要求 真题举例 命题角度 ‎1.了解向量的实际背景；‎ ‎2.理解平面向量的概念，理解两个向量相等的含义；‎ ‎3.理解向量的几何表示；‎ ‎4.掌握向量加法、减法的运算，并理解其几何意义；‎ ‎5.掌握向量数乘的运算及其几何意义，理解两个向量共线的含义；‎ ‎6.了解向量线性运算的性质及其几何意义。‎ ‎2015，全国卷Ⅰ，7,5分(平面向量的线性运算)‎ ‎2015，全国卷Ⅱ，13,5分(平面向量的线性运算)‎ ‎2014，北京卷，10,5分(平面向量的线性运算)‎ ‎2014，浙江卷，8,5分(平面向量的概念)‎ 高考对本讲内容的考查以向量的线性运算为主；以向量的概念和线性运算知识为载体，与三角函数等知识综合考查的可能性较大，复习时应予以关注。试题多为客观题，难度不大，分值约为5分。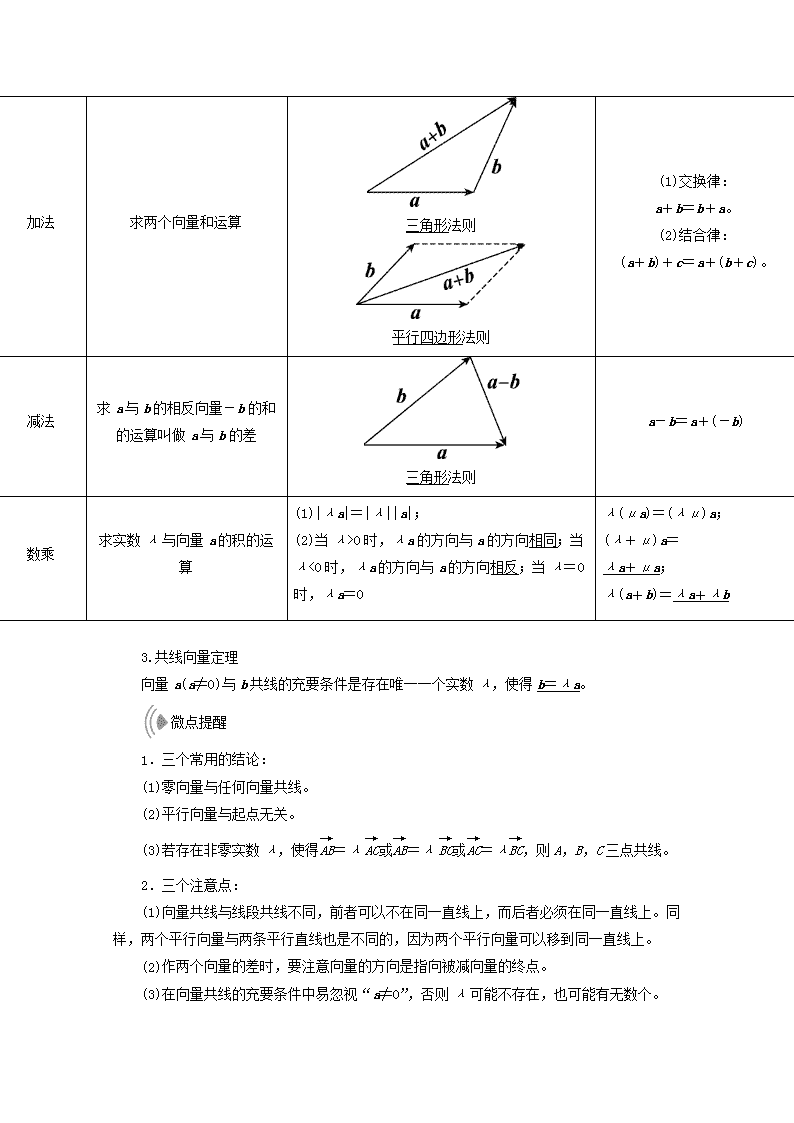‎ 微知识　小题练 自|主|排|查 ‎1．向量的有关概念 名称 定义 备注 向量 既有大小又有方向的量；向量的大小叫做向量的长度(或称模)‎ 平面向量是自由向量 零向量 长度为零的向量，其方向是任意的 记作0‎ 单位向量 长度等于1个单位的向量 非零向量a的单位向量为± 平行向量 方向相同或相反的非零向量 ‎0与任一向量平行或共线 共线向量 方向相同或相反的非零向量，又叫做共线向量 相等向量 长度相等且方向相同的向量 两向量只有相等或不等，不能比较大小 相反向量 长度相等且方向相反的向量 ‎0的相反向量为0‎ ‎2．向量的线性运算 向量 运算 定义 法则 ‎(或几何意义)‎ 运算律 加法 求两个向量和运算 三角形法则 平行四边形法则 ‎(1)交换律：‎ a＋b＝b＋a。‎ ‎(2)结合律：‎ ‎(a＋b)＋c＝a＋(b＋c)。‎ 减法 求a与b的相反向量－b的和的运算叫做a与b的差 三角形法则 a－b＝a＋(－b)‎ 数乘 求实数λ与向量a的积的运算 ‎(1)|λa|＝|λ||a|；‎ ‎(2)当λ>0时，λa的方向与a的方向相同；当λ<0时，λa的方向与a的方向相反；当λ＝0时，λa＝0‎ λ(μa)＝(λμ)a；‎ ‎(λ＋μ)a＝‎ λa＋μa；‎ λ(a＋b)＝λa＋λb ‎3.共线向量定理 向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ，使得b＝λa。‎ 微点提醒 ‎1．三个常用的结论：‎ ‎(1)零向量与任何向量共线。‎ ‎(2)平行向量与起点无关。‎ ‎(3)若存在非零实数λ，使得＝λ或＝λ或＝λ，则A，B，C三点共线。‎ ‎2．三个注意点：‎ ‎(1)向量共线与线段共线不同，前者可以不在同一直线上，而后者必须在同一直线上。同样，两个平行向量与两条平行直线也是不同的，因为两个平行向量可以移到同一直线上。‎ ‎(2)作两个向量的差时，要注意向量的方向是指向被减向量的终点。‎ ‎(3)在向量共线的充要条件中易忽视“a≠‎0”‎，否则λ可能不存在，也可能有无数个。‎ 小|题|快|练 一 、走进教材 ‎1．(必修4P‎78A组T5改编)已知三角形ABC，用与表示BC边上的中线向量，则＝________。‎ ‎【解析】　＝＋＝＋ ‎＝＋(－)＝＋。‎ ‎【答案】　＋ ‎2．(必修4P‎92A组T11改编)在四边形ABCD中，＝a＋2b，＝－‎4a－b，＝－‎5a－3b，其中a，b不共线，则四边形ABCD为(　　)‎ A．平行四边形 B．矩形 C．梯形 D．菱形 ‎【解析】　因为＝＋＋＝－‎8a－2b＝2，所以∥，且||≠||，所以四边形ABCD为梯形。故选C。‎ ‎【答案】　C 二、双基查验 ‎1．若向量a与b不相等，则a与b一定(　　)‎ A．有不相等的模 B．不共线 C．不可能都是零向量 D．不可能都是单位向量 ‎【解析】　因为所有的零向量都是相等的向量，故选C。‎ ‎【答案】　C ‎2．若m∥n，n∥k，则向量m与向量k(　　)‎ A．共线 B．不共线 C．共线且同向 D．不一定共线 ‎【解析】　若m∥0,0∥k，则k与m不一定共线，故选D。‎ ‎【答案】　D ‎3．若向量a，b满足|a|＝3，|b|＝8，则|a＋b|的最小值为(　　)‎ A．11 B．2‎ C．4 D．5‎ ‎【解析】　当a与b共线且反向时，|a＋b|的最小值为5。故选D。‎ ‎【答案】　D ‎4．已知a，b是非零向量，若|a＋b|＝|a－b|，则以a，b为邻边构成的四边形的形状为________。‎ ‎【解析】　如图，在以a与b为邻边的四边形中，|a＋b|与|a－b|分别为四边形的两条对角线，故由对角线长相等的平行四边形是矩形可知，以a，b为邻边的四边形是矩形。‎ ‎【答案】　矩形 ‎5．已知a与b是两个不共线向量，且向量a＋λb与－(b－‎3a)共线，则λ＝________。‎ ‎【解析】　由已知得a＋λb＝－k(b－‎3a)，‎ ‎∴解得 ‎【答案】　－ 微考点　大课堂 考点一 ‎ 平面向量的有关概念 ‎【典例1】　给出下列四个命题：‎ ‎①若|a|＝|b|，则a＝b或a＝－b；‎ ‎②若＝，则四边形ABCD为平行四边形；‎ ‎③若a与b同向，且|a|＞|b|，则a＞b；‎ ‎④λ，μ为实数，若λa＝μb，则a与b共线。‎ 其中假命题的个数为(　　)‎ A．1　　　　 B．‎2　‎　　　‎ C．3　　　　 D．4‎ ‎【解析】　①不正确。|a|＝|b|但a，b的方向不确定，故a，b不一定相等；②不正确。因为＝，A，B，C，D可能在同一直线上，所以ABCD不一定是四边形；③不正确。两向量不能比较大小；④不正确。当λ＝μ＝0时，a与b可以为任意向量，满足λa＝μb，但a与b不一定共线。故选D。‎ ‎【答案】　D 反思归纳　(1)正确理解向量的相关概念及其含义是解题的关键。‎ ‎(2)相等向量具有传递性，非零向量的平行也具有传递性。‎ ‎(3)共线向量即平行向量，它们均与起点无关。‎ ‎(4)向量可以平移，平移后的向量与原向量是相等向量。解题时，不要把它与函数图象平移混为一谈。‎ ‎(5)非零向量a与的关系：是a方向上的单位向量。‎ ‎【变式训练】　下列命题中正确的是(　　)‎ A．a与b共线，b与c共线，则a与c也共线 B．任意两个相等的非零向量的始点与终点是一个平行四边形的四个顶点 C．向量a与b不共线，则a与b都是非零向量 D．有相同起点的两个非零向量不平行 ‎【解析】　由于零向量与任一向量都共线，所以A不正确；由于数学中研究的向量是自由向量，所以两个相等的非零向量可以在同一直线上，而此时就构不成四边形，所以B不正确；向量的平行只要求方向相同或相反，与起点是否相同无关，所以D不正确；对于C，其条件以否定形式给出，所以可从其逆否命题入手来考虑，假设a与b不都是非零向量，即a与b中至少有一个是零向量，而由零向量与任一向量都共线，可知a与b共线，符合已知条件，所以有向量a与b不共线，则a与b都是非零向量，故选C。‎ ‎【答案】　C 考点二 ‎ 平面向量的线性运算…………母题发散 ‎【典例2】　(1)(2015·全国卷Ⅰ)设D为△ABC所在平面内一点，＝3，则(　　)‎ A.＝－＋ B.＝－ C.＝＋ D.＝－ ‎(2)设D，E分别是△ABC的边AB，BC上的点，AD＝AB，BE＝BC。若＝λ1＋λ2(λ1，λ2为实数)，则λ1＋λ2的值为________。‎ ‎【解析】　(1)＝＋＝＋＝＋(－)＝－＝－＋。故选A。‎ ‎(2)＝＋＝＋＝＋(＋)＝－＋，所以λ1＝－，λ2＝，即λ1＋λ2＝。‎ ‎【答案】　(1)A　(2) ‎【母题变式】　若将本典例(2)的条件改为“＝2，＝＋λ”，则λ＝________。‎ ‎【解析】　∵＝＋，＝＋，‎ ‎∴2＝＋＋＋。‎ 又∵＝2，‎ ‎∴2＝＋＋ ‎＝＋＋(－)‎ ‎＝＋。‎ ‎∴＝＋，即λ＝。‎ ‎【答案】　 反思归纳　平面向量线性运算问题的常见类型及解题策略 ‎(1)向量加法或减法的几何意义。向量加法和减法均适合三角形法则。‎ ‎(2)求已知向量的和。一般共起点的向量求和用平行四边形法则；求差用三角形法则；求首尾相连向量的和用三角形法则。‎ ‎(3)求参数问题可以通过研究向量间的关系，通过向量的运算将向量表示出来，进行比较求参数的值。‎ ‎【拓展变式】　(2017·惠州模拟)已知点O，A，B不在同一条直线上，点P为该平面上一点，且＝，则(　　)‎ A．点P在线段AB上 B．点P在线段AB的反向延长线上 C．点P在线段AB的延长线上 D．点P不在直线AB上 ‎【解析】　＝＝－＝＋(－)＝＋，即－＝＝，所以点P在线段AB的反向延长线上。故选B。‎ ‎【答案】　B 考点三 ‎ 共线定理的应用…………多维探究 角度一：共线定理的简单运用 ‎【典例3】　设两个非零向量e1和e2不共线。‎ ‎(1)如果＝e1－e2，＝3e1＋2e2，＝－8e1－2e2，求证：A，C，D三点共线；‎ ‎(2)如果＝e1＋e2，＝2e1－3e2，＝3e1－ke2，且A，C，F三点共线，求k的值。‎ ‎【解析】　(1)证明：＝e1－e2，＝3e1＋2e2，‎ ‎∴＝＋＝4e1＋e2，又＝－8e1－2e2，‎ ‎∴＝－2，∴与共线。‎ 又∵与有公共点C，∴A，C，D三点共线。‎ ‎(2)∵＝e1＋e2，＝2e1－3e2，‎ ‎∴＝＋＝3e1－2e2。‎ ‎∵A，C，F三点共线，‎ ‎∴∥，从而存在实数λ，使得＝λ。‎ ‎∴3e1－2e2＝3λe1－λke2。‎ 又e1，e2是不共线的非零向量，‎ ‎∴因此k＝2。∴实数k的值为2。‎ ‎【答案】　(1)见解析　(2)2‎ 角度二：利用共线定理解决几何问题 ‎【典例4】　(2016·江西九校联考)已知P是△ABC内一点，且＝＋，△PBC的面积是2 015，则△PAB的面积是________。‎ ‎【解析】　设S△ABC＝S，S△BPC＝S1＝2 015，S△APB＝S2。‎ ‎(恰当切入，从“三点共线”突破)如图，延长AP交BC于D，由平面几何知识，得＝。‎ 由A，P，D三点共线，可得＝μ＝μ＋μ(μ∈R)。①‎ 由B，D，C三点共线，可得＝λ＋(1－λ)(λ∈R)。②‎ 联立①和②，有解得 则＝μ＝，＝－＝，‎ 那么＝，于是S＝S1。‎ 同理，延长CP交AB于E，计算可得＝，‎ 所以S2＝S。‎ 于是S2＝S＝×S1＝S1＝×2 015＝2 821。‎ ‎【答案】　2 821‎ 反思归纳　利用共线向量定理解题的方法 ‎(1)证明向量共线，对于向量a，b(b≠0)，若存在实数λ，使a＝λb，则a与b共线。‎ ‎(2)证明三点共线，若存在实数λ，使＝λ，则A，B，C三点共线。‎ ‎(3)利用共线定理解决几何问题要注意两直线相交必然存在两组三点共线，通过列方程组往往能把问题解决。‎ 微考场　新提升 ‎1．(2016·开封一模)在△ABC中，M为边BC上任意一点，N为AM的中点，＝λ＋μ，则λ＋μ的值为(　　)‎ A. B. C. D．1‎ 解析　依题意＝＝λ＋μ，因为M，B，C三点共线，所以λ＋μ＝。故选A。‎ 答案　A ‎2．下列各式不能化简为的是(　　)‎ A．(＋)＋ ‎ B．(＋)＋(＋)‎ C.＋－ ‎ D.－＋ 解析　对于A，(＋)＋＝(＋)＋＝＋＝；对于B，(＋)＋(＋)＝＋(＋＋)＝；对于C，＋－＝＋2；对于D，－＋＝＋＝。故选C。‎ 答案　C ‎3．设P为锐角△ABC的外心(三角形外接圆的圆心)，＝k(＋)(k∈R)，若cos∠BAC＝，则k＝(　　)‎ A. B. C. D. 解析　取BC的中点D，连接PD，AD，则PD⊥BC，＋＝2，∵＝k(＋)(k∈R)，∴＝2k，‎ ‎∴A，P，D三点共线，‎ ‎∴AB＝AC，‎ ‎∴cos∠BAC＝cos∠DPC＝＝＝，‎ ‎∴AP＝AD，∴2k＝，解得k＝。故选A。‎ 答案　A ‎4．已知a，b是两个不共线的非零向量，且a与b起点相同。若a，tb，(a＋b)三向量的终点在同一直线上，则t＝________。‎ 解析　∵a，tb，(a＋b)三向量的终点在同一条直线上，且a与b起点相同。‎ ‎∴a－tb与a－(a＋b)共线，‎ 即a－tb与a－b共线，‎ ‎∴存在实数λ，使a－tb＝λ，‎ ‎∴解得λ＝，t＝，‎ 即t＝时，a，tb，(a＋b)三向量的终点在同一条直线上。‎ 答案　 ‎5.如图所示，在△ABC中，点O是BC的中点，过点O的直线分别交直线AB，AC于不同的两点M，N，若＝m，＝n，则m＋n的值为________。‎ 解析　＝(＋)＝＋。‎ ‎∵M，O，N三点共线，∴＋＝1。‎ ‎∴m＋n＝2。‎ 答案　2‎