【数学】2018届一轮复习北师大版第五章数列第一节数列的概念与简单表示法教案 10页

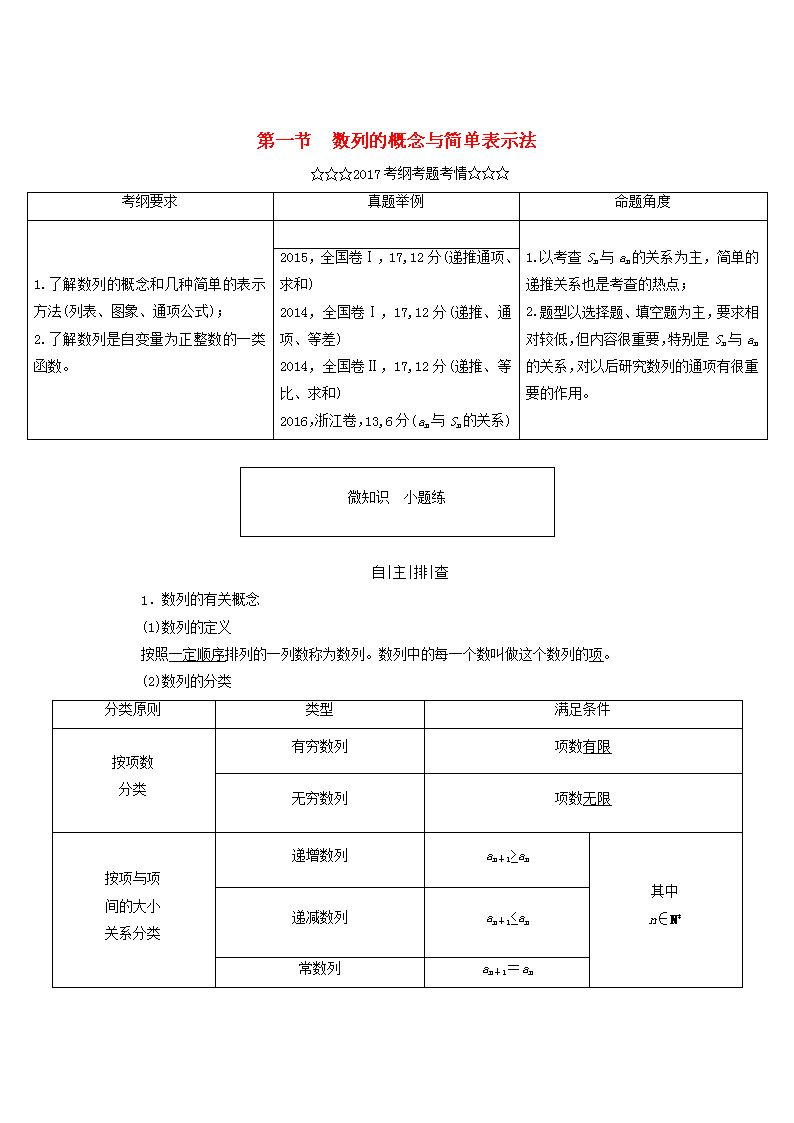
第一节　数列的概念与简单表示法 ‎☆☆☆2017考纲考题考情☆☆☆‎ 考纲要求 真题举例 命题角度 ‎1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式)；‎ ‎2.了解数列是自变量为正整数的一类函数。‎ ‎1.以考查Sn与an的关系为主，简单的递推关系也是考查的热点；‎ ‎2.题型以选择题、填空题为主，要求相对较低，但内容很重要，特别是Sn与an的关系，对以后研究数列的通项有很重要的作用。‎ ‎2015，全国卷Ⅰ，17,12分(递推通项、求和)‎ ‎2014，全国卷Ⅰ，17,12分(递推、通项、等差)‎ ‎2014，全国卷Ⅱ，17,12分(递推、等比、求和)‎ ‎2016，浙江卷，13,6分(an与Sn的关系)‎ 微知识　小题练 自|主|排|查 ‎1．数列的有关概念 ‎(1)数列的定义 按照一定顺序排列的一列数称为数列。数列中的每一个数叫做这个数列的项。‎ ‎(2)数列的分类 分类原则 类型 满足条件 按项数 分类 有穷数列 项数有限 无穷数列 项数无限 按项与项 间的大小 关系分类 递增数列 an＋1>an 其中 n∈N*‎ 递减数列 an＋10，即an＋1>an；‎ 当n＝9时，an＋1－an＝0，即an＋1＝an；‎ 当n>9时，an＋1－an<0，即an＋1a11>a12>…，‎ ‎∴数列{an}有最大项a9或a10，其值为10·9，其项数为9或10。‎ ‎【答案】　数列{an}中有最大项a9或a10，其值为10·9，其项数为9或10。‎ 反思归纳　1.解决数列的单调性问题可用以下两种方法 ‎(1)作差比较法：根据an＋1－an的符号判断数列{an}是递增数列、递减数列或是常数列。 ‎ ‎(2)作商比较法：根据(an>0或an<0)与1的大小关系进行判断。‎ ‎2．解决数列周期性问题的方法 先根据已知条件求出数列的前几项，确定数列的周期，再根据周期性求值。‎ 微考场　新提升 ‎1．若数列an＝＋＋…＋，则a5－a4＝(　　)‎ A.　　　 B．－　　　‎ C.　　　 D. 解析　∵a5＝＋＋＋＋，‎ a4＝＋＋＋，‎ ‎∴a5－a4＝＋－＝。故选C。‎ 答案　C ‎2．已知数列{an}的前n项和Sn＝，则a3＋a4等于(　　)‎ A. B. ‎ C. D. 解析　a3＋a4＝S4－S2＝－＝。故选D。‎ 答案　D ‎3．已知数列{an}的通项公式为an＝n2－2λn(n∈N*)，则“λ<‎1”‎是“数列{an}为递增数列”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 解析　若数列{an}为递增数列，则有an＋1－an>0，即2n＋1>2λ对任意的n∈N*都成立，于是有3>2λ，λ<。由λ<1可推得λ<，但反过来，由λ<不能得到λ<1，因此“λ<1”是“数列{an}为递增数列”的充分不必要条件，故选A。‎ 答案　A ‎4．数列{an}中，已知a1＝1，a2＝2，an＋1＝an＋an＋2(n∈N*)，则a7＝________。‎ 解析　由已知an＋1＝an＋an＋2，a1＝1，a2＝2，‎ 能够计算出a3＝1，a4＝－1，a5＝－2，a6＝－1，‎ a7＝1。‎ 答案　1‎ ‎5．已知数列{an}的前n项和为Sn，Sn＝2an－n，则an＝________。‎ 解析　当n＝1时，S1＝a1＝‎2a1－1，得a1＝1，当n≥2时，an＝Sn－Sn－1＝2an－n－2an－1＋(n－1)，‎ 即an＝2an－1＋1，∴an＋1＝2(an－1＋1)，‎ ‎∴数列{an＋1}是首项为a1＋1＝2，公比为2的等比数列，‎ ‎∴an＋1＝2·2n－1＝2n，∴an＝2n－1。‎ 答案　2n－1‎