山东省潍坊高密市2020届高三模拟数学试题二 Word版含解析 26页

- 1 - 数学模拟试题二 第 I 卷 选择题部分（共 60 分） 一、选择题：本大题共 8 小题，每小题 5 分，共 40 分.在每小题给出的四个选项中， 只有一项是符合题目要求的. 1.设全集为 R ，集合  2| 4M x x  ，  0,1,2N  ，则 M N  （ ） A.  0,1,2 B. (0,2) C. ( 2,2) D.  0,1 【答案】D 【解析】 【分析】 可解出 M，然后进行交集的运算即可． 【详解】解：M＝{x|﹣2＜x＜2}，N＝{0，1，2}； ∴M∩N＝{0，1}． 故选 D． 【点睛】本题考查描述法、列举法的定义，以及交集的运算，属于基础题． 2.已知复数 1 1 iz   ，则 z i 在复平面内对应的点位于（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】A 【解析】 【分析】 直接利用复数代数形式的除法运算化简，计算得到复数 z i 对应的点，则答案可求． 【详解】∵ 1 1 1 2 iz i   ， ∴ 1 1=2 2 i iz i i    . ∴ z i 在复平面内对应的点为 1 1,2 2      ， ∴ z i 在复平面内对应的点位于第一象限. 故选：A. 【点睛】本题考查复数的代数表示法及其几何意义，属于简单题. - 2 - 3.近年来，随着“一带一路”倡议的推进，中国与沿线国家旅游合作越来越密切，中国到“一带 一路”沿线国家的游客人也越来越多，如图是 2013－2018 年中国到“一带一路”沿线国家的游客 人次情况，则下列说法正确的是（ ） ①2013－2018 年中国到“一带一路”沿线国家的游客人次逐年增加 ②2013－2018 年这 6 年中，2014 年中国到“一带一路”沿线国家的游客人次增幅最小 ③2016－2018 年这 3 年中，中国到“一带一路”沿线国家的游客人次每年的增幅基本持平 A. ①②③ B. ②③ C. ①② D. ③ 【答案】A 【解析】 【分析】 根据折线图，分析图中的数据逐一判断即可. 【详解】由图中折线逐渐上升，即每年游客人次逐渐增多，故①正确； 由图在 2014 年中折线比较平缓，即 2014 年中游客人次增幅最小，故②正确； 根据图像在 2016－2018 年这 3 年中，折线的斜率基本相同， 故每年的增幅基本持平，故③正确； 故选：A 【点睛】本题考查了折线图，考查了统计与推理，属于基础题. 4.平面向量 a 与b 的夹角为 60，且 3a  ， b 为单位向量，则 2a b   （ ） A. 3 B. 19 C. 19 D. 2 3 【答案】B 【解析】 【分析】 - 3 - 计算 2 2 19a b   ，得到答案. 【详解】  22 2 2 2 2 = 4 4 9 6 4 19a b a b a a b b                 ，故 2 19a b   . 故选： B . 【点睛】本题考查了向量模的计算，意在考查学生的计算能力. 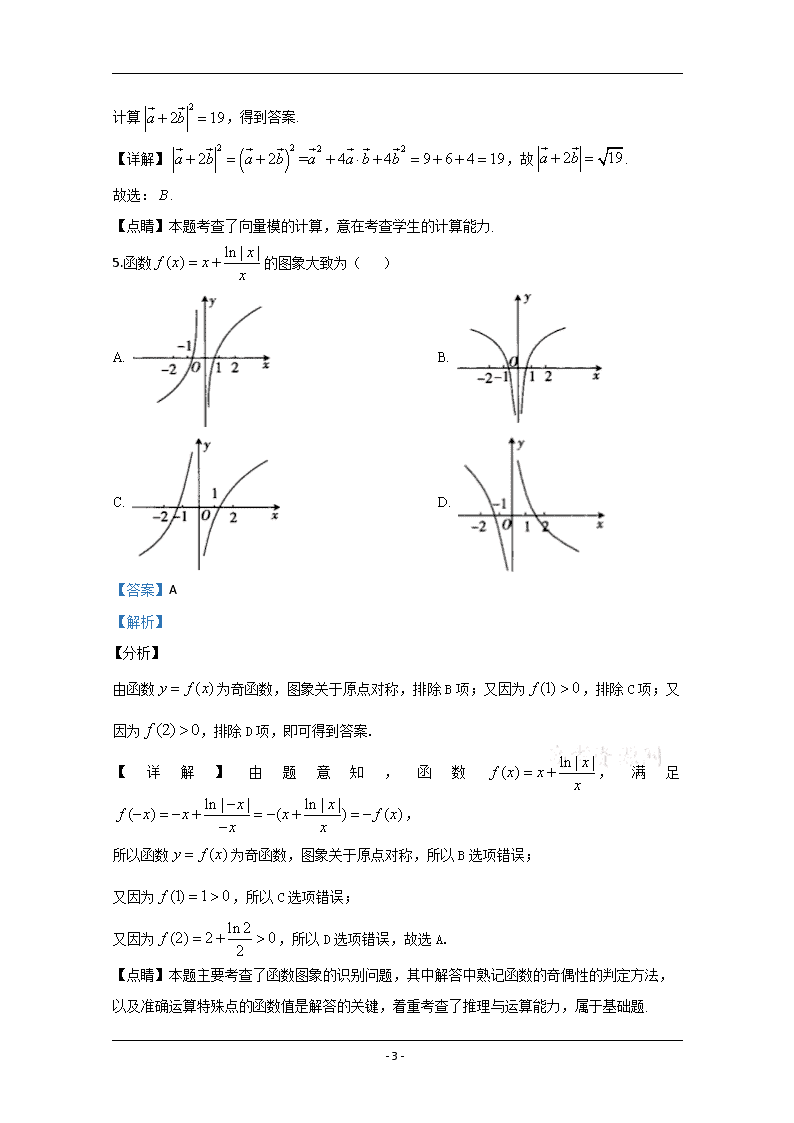5.函数 ln | |( ) xf x x x   的图象大致为（ ） A. B. C. D. 【答案】A 【解析】 【分析】 由函数 ( )y f x 为奇函数，图象关于原点对称，排除 B 项；又因为 (1) 0f  ，排除 C 项；又 因为 (2) 0f  ，排除 D 项，即可得到答案. 【 详 解 】 由 题 意 知 ， 函 数 ln | |( ) xf x x x   ， 满 足 ln | | ln | |( ) ( ) ( )x xf x x x f xx x          ， 所以函数 ( )y f x 为奇函数，图象关于原点对称，所以 B 选项错误； 又因为 (1) 1 0f   ，所以 C 选项错误； 又因为 ln 2(2) 2 02f    ，所以 D 选项错误，故选 A. 【点睛】本题主要考查了函数图象的识别问题，其中解答中熟记函数的奇偶性的判定方法， 以及准确运算特殊点的函数值是解答的关键，着重考查了推理与运算能力，属于基础题. - 4 - 6.已知角 的终边经过点  3, 4P  ，则 tan2  （ ） A. 12 7 B. 12 7  C. 24 7 D. 24 7  【答案】C 【解析】 【分析】 利用任意角的三角函数的定义先求出 tan ，由二倍角的公式可求出 tan 2 的值． 【详解】解：角 的终边经过点  3, 4P  ， 由任意角的三角函数的定义得： 4tan 3    ， 故有 2 2tan 24tan 2 1 tan 7    . 故选：C． 【点睛】本题考查任意角的三角函数的定义，二倍角公式的应用，考查计算能力． 7.已知双曲线 2 2 2 12 x y a   的一条渐近线的倾斜角为 6  ，则双曲线的离心率为（ ） A. 2 3 3 B. 2 6 3 C. 3 D. 2 【答案】A 【解析】 【分析】 求出双曲线的渐进线方程，可得到 a 值，再由 , ,a b c 的关系和离心率公式，即可得到答案． 【详解】双曲线 2 2 2 12 x y a   的一条渐近线的倾斜角为 6  ， 则 3tan 6 3   ， 所以该条渐近线方程为 3 3y x ； 所以 2 3 3a  ， - 5 - 解得 6a  ； 所以 2 2 6 2 2 2c a b     ， 所以双曲线的离心率为 2 2 2 3 36 ce a    ． 故选 A． 【点睛】本题考查双曲线的方程与性质，考查离心率的求法，考查学生基本的运算能力，属 于基础题， 8.已知椭圆 2 2 2 2: 1( 0)x yG a ba b     的右焦点为 F(3,0)，过点 F 的直线交椭圆于 A,B 两点.若 AB 的中点坐标为（1，-1），则 G 的方程为（ ） A. 2 2 145 36 x y  B. 2 2 136 27 x y  C. 2 2 127 18 x y  D. 2 2 118 9 x y  【答案】D 【解析】 【分析】 设出 ,A B 两点的坐标，利用点差法求得 ,a b 的关系式，结合 2 2 2a b c  求得 2 2,a b ，进而求 得椭圆 E 的方程. 【详解】设    1 1 2 2, , ,A x y B x y ，则 2 2 1 1 2 2 2 2 2 2 2 2 1 1 x y a b x y a b       ，两式相减并化简得 2 1 2 1 2 2 1 2 1 2 y y y yb a x x x x      ， 即  2 2 2 2 2 2 0 11 1 1 21 3 1 2 2 b b a ba a           , 由于 2 2 2a b c  且 3c  ，由此可解得 2 218, 9a b  ， 故椭圆 E 的方程为 2 2 118 9 x y  . - 6 - 故选：D. 【点睛】本小题主要考查点差法解决椭圆中的中点弦问题，属于基础题. 二、多项选择题：本大题共 4 小题，每小题 5 分，共 20 分.在每小题给出的四个选 项中，有多项符合题目要求.全部选对得 5 分，部分选对得 3 分，有选错的得 0 分. 9.若函数   1xf x e  与  g x ax 的图象恰有一个公共点，则实数 a 可能取值为（ ） A. 2 B. 0 C. 1 D. 1 【答案】BCD 【解析】 【分析】 作出   1xf x e  的图像，利用数形结合可判断 0a  满足恰有一个公共点；当 0a  时，需 直线与曲线相切即可. 【详解】 由   1xf x e  与  g x ax 恒过 0,0 ，如图， 当 0a  时，两函数图象恰有一个公共点， 当 0a  时，函数   1xf x e  与  g x ax 的图象恰有一个公共点， 则  g x ax 为   1xf x e  的切线，且切点为 0,0 ， 由   xf x e  ，所以   00 1a f e   ， 综上所述， 0, 1a   或1. 故选：BCD 【点睛】本题考查了指数函数图像、导数的几何意义，考查了数形结合在解题中的应用，属 于基础题. - 7 - 10.设正项等差数列 na 满足 2 1 10 2 92 20a a a a   ，则（ ） A. 2 9a a 的最大值为10 B. 2 9a a 的最大值为 2 10 C. 2 2 2 9 1 1 a a  的最大值为 1 5 D. 4 4 2 9a a 的最小值为 200 【答案】ABD 【解析】 【分析】 根据等差数列的性质，求得 2 9,a a 的关系式，由此结合基本不等式，判断出正确选项. 【详解】因为正项等差数列 na 满足 2 1 10 2 92 20a a a a   ， 所以 2 2 9 2 92 20a a a a   ， 即 2 2 2 9 20a a  . ① 2 2 2 9 2 9 20 102 2 a aa a    ，当且仅当 2 9 10a a  时成立，故 A 选项正确. ②由于 2 2 2 2 9 2 9 102 2 a a a a       ，所以 2 9 2 910, 2 102 a a a a    ，当且仅当 2 9 10a a  时成立，故 B 选项正确. ③ 2 2 2 9 22 2 2 2 2 2 22 22 9 2 9 2 9 2 9 1 1 20 20 20 1 10 5 2 a a a a a a a a a a             ，当且仅当 2 9 10a a  时成立， 所以 2 2 2 9 1 1 a a  的最小值为 1 5 ，故 C 选项错误. ④结合①的结论，有  24 4 2 2 2 2 2 2 2 2 9 2 9 2 9 2 92 400 2 400 2 10 200a a a a a a a a            ， 当且仅当 2 9 10a a  时成立，故 D 选项正确. 故选：ABD 【点睛】本小题主要考查等差数列的性质，考查基本不等式求最值，属于中档题. 11.过抛物线 2: 8C y x 的焦点 F 且斜率为 3 的直线l 与抛物线交于 ,P Q 两点（ P 在第一象 - 8 - 限），以 ,PF QF 为直径的圆分别与 y 轴相切于 ,A B 两点，则下列结论正确的是（ ） A. 抛物线 2: 8C y x 的焦点 F 坐标为 (2,0) B. 32| | 3PQ  C. M 为抛物线C 上的动点， (2,1)N ，则 min(| | | |) 6MF MN  D. 8 3| | 3AB  【答案】ABD 【解析】 【分析】 A，由抛物线方程可得焦点坐标；B，由题意可得直线 PQ 的方程与抛物线联立求出 P，Q 的 坐标，进而可得 PQ 的长度；C，由抛物线的性质到焦点的距离等于到准线的距离距离可得 |MF|+|MN|的最小值；D，由题意可得 A，B 的坐标，进而求出 AB 的值；然后判断所给命题的 真假． 【详解】A，由题意可得抛物线的焦点 F（2，0），所以 A 正确； B，由题意设直线 PQ 的方程为：y 3 （x﹣2）， 与抛物线联立整理可得：3x2﹣20x+12＝0，解得：x 2 3  或 6， 代入直线 PQ 方程可得 y 分别为： 4 3 3  ，4 3 ， 由题意可得 P（6，4 3 ），Q（ 2 3 ， 4 3 3  ）； 所以|PQ|＝6 2 3   4 32 3  ，所以 B 正确； C，如图 M 在抛物线上，ME 垂直于准线交于 E，可得|MF|＝ME|， 所以|MF|+|MN|＝|ME|+|MN|≥NE＝2+2＝4，当 N，M，E 三点共线时，|MF|+|MN|最小，且最小 值为 4，所以 C 不正确； D，因为 P（6，4 3 ），Q（ 2 3 ， 4 3 3  ），所以 PF，QF 的中点分别为：（3，2 3 ），（ 1 3 ， 2 3 3  ）， 所以由题意可得 A（0，2 3 ），B（0， 2 3 3  ）， - 9 - 所以|AB|＝2 2 3 8 33 3 3   ，所以 D 正确； 故选：ABD． 【点睛】本题主要考查抛物线的性质，考查直线和抛物线的位置关系，考查抛物线的最值的 解答，意在考查学生对这些知识的理解掌握水平，属于中档题． 12.在边长为 2 的等边三角形 ABC 中，点 ,D E 分别是边 ,AC AB 上的点，满足 //DE BC 且 AD AC  ，（  01  ， ），将 ADE 沿直线 DE 折到 A DE△ 的位置.在翻折过程中，下列结论 不成立的是（ ） A. 在边 A E 上存在点 F ，使得在翻折过程中，满足 //BF 平面 A CD B. 存在 10 2       , ，使得在翻折过程中的某个位置，满足平面 A BC  平面 BCDE C. 若 1 2   ，当二面角 A DE B  为直二面角时，| | 10 4A B  D. 在翻折过程中，四棱锥 A BCDE 体积的最大值记为  f  ，  f  的最大值为 2 3 9 【答案】ABC 【解析】 【分析】 对于 A.在边 A E 上点 F，在 A D 上取一点 N，使得 / /FN ED ，在 ED 上取一点 H，使得 / /NH EF ，作 / /HG BE 交 BC 于点 G，即可判断出结论. 对于 B， 10 2       , ，在翻折过程中，点 A在底面 BCDE 的射影不可能在交线 BC 上，即可 判断出结论. - 10 - 对于C， 1 2   ，当二面角 A DE B  为直二面角时，取ED的中点M，可得 AM  平面 BCDE . 可得 2 2A B AM BM   ，结合余弦定理即可得出. 对于 D.在翻折过程中，取平面 AED  平面 BCDE ，四棱锥 A BCDE 体积   31 33 BCDEf S        ，  01  ， ，利用导数研究函数的单调性即可得出. 【详解】对于 A.在边 A E 上点 F，在 A D 上取一点 N，使得 / /FN ED ，在 ED 上取一点 H， 使得 / /NH EF ，作 / /HG BE 交 BC 于点 G，如图所示， 则可得 FN 平行且等于 BG ，即四边形 BGNF 为平行四边形， ∴ / /NG BE ，而 GN 始终与平面 ACD 相交， 因此在边 A E 上不存在点 F，使得在翻折过程中，满足 //BF 平面 A CD ，A 不正确. 对于 B， 10 2       , ，在翻折过程中，点 A在底面 BCDE 的射影不可能在交线 BC 上，因此 不满足平面 A BC  平面 BCDE ，因此 B 不正确. 对于 C. 1 2   ，当二面角 A DE B  为直二面角时，取 ED 的中点 M，如图所示： 可得 AM  平面 BCDE ， 则 2 2 2 23 1 1 10 10( ) 1 ( ) 2 1 cos1202 2 2 2 4A B AM BM             ，因此 C - 11 - 不正确； 对于 D.在翻折过程中，取平面 AED⊥平面 BCDE，四棱锥 A BCDE 体积   31 33 BCDEf S        ，  01  ， ，   21 3f     ，可得 3 3   时，函数  f  取得最大值   3 1 2 313 3 9f        ，因此 D 正确. 综上所述，不成立的为 ABC. 故选：ABC. 【点睛】本题考查了利用运动的观点理解空间线面面面位置关系、四棱锥的体积计算公式、 余弦定理、利用导数研究函数的单调性极值与最值，考查了推理能力空间想象能力与计算能 力，属于难题. 第 II 卷 非选择题部分（共 90 分） 三、填空题：本大题共 4 小题，每小题 5 分，共 20 分. 13.若直线 2y x b  是曲线 2 lny a x 的切线，且 0a  ，则实数 b 的最小值是______. 【答案】 2 【解析】 【分析】 求出 2 lny a x 的导数，设切线为 ( , )m n ，由切点处的导数值为切线斜率求出 m a ，再由 切点坐标可把b 表示为 a 的函数，再利用导数可求得b 的最小值． 【详解】 2 lny a x 的导数为 2ay x   ，由于直线 2y x b  是曲线 2 lny a x 的切线，设 切点为 ,m n ，则 2 2a m  ， ∴ m a ，又 2 2 lnm b a m  ，∴ 2 ln 2b a a a  （ 0a  ），  2 ln 1 2 2lnb a a     ， 当 1a  时， 0b  ，函数 b 递增，当 0 1a  时， 0b  ，函数 b 递减， ∴ 1a  为极小值点，也为最小值点，∴b 的最小值为 2ln1 2 2   . 故答案为： 2 ． 【点睛】本题考查导数的几何意义，考查用导数求函数的最值．在求切线方程时要注意“在” 某点处的切线与“过”某点的切线．如果是过某点的切线可设切点坐标为 0 0( , )x y ，利用导数 - 12 - 几何意义求出切点坐标． 14.已知函数 1( ) cos2 2 sin cos2 2 2 4 x x af x x a   （ 0 2x   ）的最大值为 3 2 4 a  ，则实数 a 的取值范围是______________. 【答案】 2a  【解析】 【分析】 通过换元法将  f x 的最值问题转化为 2 1( ) ,0 14 2 ag t t at t       的最值，利用二次函 数的性质列不等式求解即可． 【详解】解：由已知  2 21 1( ) 1 2sin sin sin sin2 4 4 2 a af x x a x x a x         令  sin 0,1t x  ， 则 2 1( ) ,0 14 2 ag t t at t       ， 因为 1 3 2(1) 1 4 2 4 a ag a       ， 则 ( )g t 在区间 0,1 的右端点取最大值， 故 12 a  ，则 2a  ． 故答案为： 2a  ． 【点睛】本题考查二次型三角函数的最值问题，通过换元法可将问题简单化，是一道基础题． 15.点 ,A B 是抛物线 2: 2 ( 0)C y px p  上的两点，F 是抛物线C 的焦点，若 120AFB   ， AB 中点 D 到抛物线C 的准线的距离为 d ，则 | | d AB 的最大值为_______. 【答案】 3 3 【解析】 【分析】 过 , ,A B D 作 准 线 的 垂 线 ， 垂 足 分 别 为 , ,N P M ， 则 1 1( ) ( )2 2d MD AN BP AF BF     ，在 ABF 中寻找它们的关系，求出比值的最 - 13 - 大值。 【详解】 如图，过 , ,A B D 作准线的垂线，垂足分别为 , ,N P M ，则 1 1( ) ( )2 2d MD AN BP AF BF     ， ABF 中， 2 2 2 2 cos120AB AF BF AF BF    2 2AF BF AF BF   2 2 2 23( ) ( ) ( ) ( )2 4 AF BFAF BF AF BF AF BF AF BF         ，当且仅当 AF BF 时取等号。 ∴ 4 2 3 3 3 AF BF AB    ， | | d AB 1 3 2 3 AF BF AB    ，即 d AB 的最大值为 3 3 。 故答案为： 3 3 。 【点睛】本题考查抛物线的定义，在抛物线中涉及到抛物线上的点到焦点的距离或弦中点到 准线的距离，可作出抛物线上点到准线的距离，让它们进行转化，象本题，弦中点到准线距 离最终转化为弦的两顶点到焦点的距离之和，然后在三角形中由余弦定理建立联系。 16.在四棱锥 P ABCD 中，PA  平面 ABCD ， 2AP  ，点 M 是矩形 ABCD 内（含边界） 的动点，且 1AB  ， 3AD  ，直线 PM 与平面 ABCD 所成的角为 4  .记点 M 的轨迹长度为  ，则 tan  ______；当三棱锥 P ABM 的体积最小时，三棱锥 P ABM 的外接球的表 面积为______. - 14 - 【答案】 (1). 3 (2). 8 【解析】 【分析】 先根据已知条件判断出点 M 的轨迹为圆弧，再求此时的 ，即可求出 tan 3  ；判断三棱 锥 P ABM 的体积最小时即点 M 位于 F 时，此时三棱锥 P ABM 的外接球球心为 PF 的 中点，所以半径为 PF 的一半，从而可得外接球的表面积. 【详解】如图，因为 PA  平面 ABCD ，垂足为 A ， 则 PMA 为直线 PM 与平面 ABCD 所成的角， 所以 4PMA   .因为 2AP  ，所以 2AM  ， 所以点 M 位于底面矩形 ABCD 内的以点 A 为圆心， 2 为半径的圆上， 记点 M 的轨迹为圆弧 EF .连接 AF ，则 2AF  . 因为 1AB  ， 3AD  ，所以 6AFB FAE     ， 则弧 EF 的长度 26 3      ，所以 tan 3  . 当点 M 位于 F 时，三棱锥 P ABM 的体积最小， 又 2PAF PBF     ， ∴三棱锥 P ABM 的外接球球心为 PF 的中点. 因为 2 22 2 2 2PF    ， 所以三棱锥 P ABM 的外接球的表面积  2 4 2 8S    . 故答案为： 3 ；8 【点睛】本题考查了由线面垂直得到线面角，判断出动点轨迹，外接球的半径及表面积的计 - 15 - 算，属于较难题. 四、解答题：本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步 骤. 17.已知递增等差数列 na 满足 1 5 10a a  ， 2 4 21a a  ，数列 nb 满足 22log 1, *n nb a n N   . （1）求 nb 的前 n 项和 nS ； （2）若 1 2( 1)n nT nb n b b    ，求数列 nT 的通项公式. 【答案】（1） 2 1n nS   （2） 12 2n nT n+ - -= 【解析】 【分析】 （1）根据等差数列公式计算得到 2 1na n  ， 12n nb  ，得到答案. （2）化简得到 1 2n nT S S S    ，代入数据计算得到答案. 【详解】（1）设数列{ }na 公差为 ( 0)d d  ，由 1 1 1 2 4 10 ( )( 3 ) 21 a d a d a d       ， 解得： 1 11 9 2 2 a a d d         或 （舍去），所以 2 1na n  ， 1 2log 1, 2n n nb n b    . 2 1 2 12 1 n n nS    . （2） 1 2( 1) ...n nT nb n b b     ， 1 1 2 1 2 3 1 2( ) ( ) ( )n nT b b b b b b b b b            2 1 2 (2 1) (2 1) + 2 1)n nS S S           （ 2 12(2 1)(2 2 +2 2 22 1 n n nn n n         ） . 【点睛】本题考查了等差数列通项公式，等比数列求和，分组求和法，意在考查学生对于数 列公式方法的综合应用. 18.已知在 ABC 中， sin sina A c C ，且 2 2 2sin sin sinB A C  . - 16 - （1）判断 ABC 的形状； （2）若 D 为 BC 的中点，BE  AD，垂足为 E，延长 BE 交 AC 于 F，求证： ADB FDC   . 【答案】（1）等腰直角三角形；（2）证明见解析 【解析】 【分析】 （1）由正弦定理得 2 2 2 2 2,a c b a c   ，进而可得 ABC 的形状； （2）以 B 为坐标原点，BC、BA 所在直线分别为 x 轴、 y 轴建立平面直角坐标系，利用向量 夹角的坐标运算得出 cos FDC ， cos ADB ，可得相等. 【详解】解：（1）由正弦定理得：sin ,sin ,2 2 a bA BR R   sin 2 cC R  ，其中 R 为 ABC 外 接圆的半径. ∵ sin sina A c C ，且 2 2 2sin sin sinB A C  ， ∴ 2 2 a ca cR R    ， 2 2 2( ) ( ) ( )2 2 2 b a c R R R   ， ∴ 2 2 2 2 2,a c b a c   ， ∴ 0, 90a c B  ， ∴ ABC 为等腰直角三角形； (2)以 B 为坐标原点，BC、BA 所在直线分别为 x 轴、 y 轴建立平面直角坐标系. 设 A（0，2），C（2，0），则 D（1，0）， (2, 2)AC   . 设 AF AC   ，则 (0 2) (2 , 2 ) 2 2 2BF BA AF             ， （ ， ）， 又因为  1,2DA   ， BF DA   ， 所以 0BF DA    ， 所以 -2 2 2 2 0   （ ） ， 解得 2 3   ， 所以 4 2( , )3 3BF  ， 所以 1 2( , )3 3DF BF BD     ，又因为 (1 0)DC  ， ， - 17 - 所以 5cos 5 DF DCFDC DF DC         ， 又因为 5cos 5 BDADB AD    ，且 ADB ， (0, )FDC   ， 所以 ADB FDC   . 【点睛】本题考查正弦定理边角互化的应用，考查向量坐标运算研究三角形中的角，是中档 题. 19.如图，在四棱锥 A DBCE 中，底面 DBCE 是等腰梯形， 2BC DE ， BD DE CE  ， ADE 是等边三角形，点 F 在 AC 上，且 3AC AF ． （1）证明： AD //平面 BEF ． （2）若平面 ADE  平面 BCED ，求二面角 F BE C  的余弦值． 【答案】（1）证明见解析；（2） 13 13 【解析】 【分析】 （1）连接 DC 交 BE 于点 G ，通过证明 DA // FG ，即可推证线面平行； （2）取 DE 中点为O ，以O 为坐标原点建立空间直角坐标系，求得对应平面的法向量，利用 向量法求二面角的余弦值即可. 【详解】（1）连接 DC 交 BE 于点 G ，连接 FG ． - 18 - ∵在等腰梯形 DBCE 中， BD DE CE  ， 2BC DE ， BC // DE ，∴ 2CG BC DG DE   ，∵ 3AC AF ，∴ 2CF AF  ， ∴ CF CG AF DG  ，∴ AD // FG ， 又 AD  平面 BEF ， FG  平面 BEF ， ∴ AD //平面 BEF ． （2）取 DE 的中点O ， BC 的中点 H ，连接 AO ，OH ，显然 AO DE ． 又平面 ADE  平面 BCED ，平面 ADE  平面 BCED DE ， 所以 AO  平面 BCED ． 因为O 、 H 分別为 DE 、 BC 的中点，且在等腰梯形 DBCE 中， 2BC DE ， 所以OH DE ．以O 为原点建立如所示的空间直角坐标系 O xyz ， 设  2 0BC a a  ，则 3, ,02B a a       ， 3, ,02C a a      ， ,0,02 aE    ， 30,0, 2A a       ， ∴ 3 3, ,02 2 aBE a         ， ∴ 2 3BF BC CF BC CA        - 19 -   2 3 3 4 3 32 ,0,0 , , , ,3 2 2 3 3 3a a a a a a a                    易得  0,0,1u  为平面 BEC 的一个法向量， 设平面 FBE 的一个法向量为  1 1 1, ,v x y z ， 可得 0 0 v BE v BF        ，故 1 1 1 1 1 3 3 02 2 4 3 3 03 3 3 a x ay ax ay az        ， 令 1 3y  ，可得 1 3x   ， 1 1z   ，则  3,3, 1v    ． 设二面角 F BE C  的平面角为 ，则 1 13cos 131 13 u v u v           ， 即二面角 F BE C  的余弦值为 13 13 ． 【点睛】本题考查由线线平行推证线面平行，利用向量法求二面角的大小，属综合中档题. 20.已知椭圆C 的中心在原点O ，焦点在 x 轴上，  0,2D 为椭圆C 短轴的一个端点， 1F 、 2F 为椭圆的左、右焦点，线段 2DF 的延长线与椭圆C 相交于点 E ，且 2 23DF EF . （1）求椭圆C 的方程； （2）如图，点 A 为椭圆上一动点（非长轴端点）， 2AF 的延长线与椭圆交于 B 点， AO 的延 长线与椭圆交于C 点，求 ABC 面积的最大值. 【答案】（1） 2 2 18 4 x y  ；（2） 4 2 . 【解析】 【分析】 - 20 - （1）根据椭圆短轴顶点求得b ；结合 2 23DF EF ，求得点 E 的坐标，根据点 E 的坐标满 足椭圆方程，结合 2 2 2a b c  ，求得 ,a c ，则椭圆方程即可求解； （2）根据直线斜率是否存在，进行分类讨论；当直线 AB 斜率存在时，设出直线方程，联立 椭圆方程，利用韦达定理，求得弦长 AB ，求得 O 到直线 AB 的距离，即可求得C 到直线 AB 的距离，利用面积公式，结合均值不等式，即可容易求得面积的最值. 【详解】（1）设椭圆C 的方程为   2 2 2 2 1 0x y a ba b     ，右焦点  2 ,0F c ， 因为  0,2D 为椭圆短轴的一个端点，则 2b  . 因为 2 23DF EF ， 故可得 23DF F E  ，设点 E 坐标为 ,x y ， 即   , 2 3 ,c x c y   ，解得 4 2,3 3 cx y   . 则点 4 2,3 3 cE     . 因为点 E 在椭圆上，则 2 2 16 1 19 9 c a   ，即 2 22a c . 又 2 2 4c a  ，则  2 22 4a a  ，得 2 8a  ， 所以椭圆C 的标准方程是 2 2 18 4 x y  . （2）①当直线 AB 的斜率不存在时，不 妨取  2, 2A ，  2, 2B  ，  2, 2C   ， 故 1 2 2 4 4 22ABCS     ； ②当直线 AB 的斜率存在时，设直线 AB 的方程为  2y k x  ，  1 1,A x y ，  2 2,B x y ， 联立方程   2 2 2 18 4 y k x x y      ，化简得  2 2 2 22 1 8 8 8 0k x k x k     ， - 21 - 则     2 2 2 264 4 2 1 8 8 32 1 0k k k k        ， 2 1 2 2 8 2 1 kx x k    ， 2 1 2 2 8 8 2 1 kx x k    ，    22 1 2 1 21 4A k x x xB x          22 2 2 2 2 8 8 81 42 1 2 1 k kk k k               2 2 14 2 2 1 k k    ， 点O 到直线  2y k x  的距离 2 2 2 2 1 1 k kd k k     ， 因为O 是线段 AC 的中点，所以点C 到直线 AB 的距离为 2 42 1 kd k   ， ∴ 2 2 2 41 1 12 4 22 2 2 1 1ABC kkS AB d k k                2 2 22 1 8 2 2 1 k k k     ， ∵             2 2 2 2 2 2 2 2 2 22 2 2 1 1 1 1 44 12 1 1 k k k k k k k kk k k            ，又 2 2 1k k  ，所以等号不成立. ∴     2 2 22 1 8 2 4 2 2 1 ABC k k S k       ， 综上可得， ABCS 面积的最大值为 4 2 . 【点睛】本题考查椭圆方程的求解，以及椭圆中面积的范围问题，属综合中档题. 21.2019 年 7 月 1 日到 3 日，世界新能源汽车大会在海南博鳌召开，大会着眼于全球汽车产业 的转型升级和生态环境的持续改善．某汽车公司顺应时代潮流，最新研发了一款新能源汽车， 并在出厂前对 100 辆汽车进行了单次最大续航里程（理论上是指新能源汽车所装载的燃料或 电池所能够提供给车行驶的最远里程）的测试．现对测试数据进行分析，得到如图的频率分 布直方图． - 22 - （1）估计这 100 辆汽车的单次最大续航里程的平均值 x （同一组中的数据用该组区间的中点 值代表）； （2）根据大量的汽车测试数据，可以认为这款汽车的单次最大续航量程 X 近似地服从正态分 布  2,N   ，经计算第（1）问中样本标准差 s 的近似值为 50．用样本平均数 x 作为  的近 似值，用样本标准差 s 作为 的估计值，现任取一辆汽车，求它的单次最大续航里程恰在 250 千米到 400 千米之间的概率； （3）某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动， 客户可根据抛掷硬币的结果，操控微型遥控车在方格图上行进，若遥控车最终停在“胜利大本 营”，则可获得购车优惠券．已知硬币出现正，反面的概率都是 1 2 ，方格图上标有第 0 格、第 1 格、第 2 格……第 50 格．遥控车开始在第 0 格，客户每掷一次硬币，遥控车向前移动一次， 若掷出正面，遥控车向前移动一格（从 k 到 1k  ），若掷出反面，遥控车向前移动两格（从 k 到 2k  ），直到遥控车移到第 49 格（胜利大本营）或第 50 格（失败大本营）时，游戏结束．设 遥控车移到第 n 格的概率为 nP ，试证明  * 1 1 49, Nn nP P n n    是等比数列，并解释 此方案能否成功吸引顾客购买该款新能源汽车． 参考数据：若随机变量 服从正态分布  2,N   ，则   0.6827P        ≤ ，  2 2 0.9545P        ≤ ，  3 3 0.9973P          ． 【答案】（1）300；（2） 0.8186 ；（3）见解析. 【解析】 【分析】 （1）利用频率分布直方图的平均数的计算方法即可得出 x ． （2）由  2300,50X N ．利用正态分布的对称性可得  250 400XP   ． - 23 - （3）遥控车移到第  2 49n n  格的情况是下面两种，而且只有两种：①遥控车先到第 2n  格，又掷出反面，其概率为 2 1 2 nP  ．②遥控车先到第 1n  格，又掷出正面，其概率为 1 1 2 nP  ．可 得： 2 1 1 1 2 2n nnP P P   ，即可得证数列 1n nP P  是等比数列，并计算获胜与失败的概率. 【详解】（1） 0.002 50 205 0.004 50 255 0.009 50 305 0.004 50 355x              0.001 50 405 300   （千米）． （2）由  2300,50X N ． ∴   0.9545 0.6827250 400 0.9545 0.81862XP      ． （3）遥控车开始在第 0 格为必然事件， 0 1P  ． 第一次掷硬币出现正面，遥控车移到第一格，其概率为 1 2 ，即 1 1 2P  ． 遥控车移到第  2 49n n  格的情况是下面两种，而且只有两种： ①遥控车先到第 2n  格，又掷出反面，其概率为 2 1 2 nP  ． ②遥控车先到第 1n  格，又掷出正面，其概率为 1 1 2 nP  ． ∴ 2 1 1 1 2 2n nnP P P   ． ∴  1 1 2 1 2n n n nP P P P     ． ∴1 49n  时，数列 1n nP P  是等比数列， 首项为 1 0 1 2P P   ，公比为 1 2  的等比数列． ∴ 1 11 2P    ， 1 2 2 1 2P P       ， 3 3 2 1 2P P       ，……， 1 1 2 n n nP P        ． ∴      1 1 2 1 0 0n n n n nP P P P P P P P          11 1 1 12 2 2 n n                 - 24 - 1 1 11 2 12 11 3 21 2 n n                        ．  0,1, ,49n   ． ∴获胜的概率 50 49 2 113 2P           ， 失败的概率 49 49 50 48 1 1 2 1 1 11 12 2 3 2 3 2P P                             ． ∴ 50 49 48 49 50 2 1 1 1 1 11 1 1 03 2 3 2 3 2P P                                             ． ∴获胜的概率大． ∴此方案能成功吸引顾客购买该款新能源汽车． 【点睛】此题考查统计与概率相关知识，根据频率分布直方图求解平均数，利用正态分布求 解概率，利用递推数列关系建立等式解决概率相关问题，综合性强. 22.已知函数   2 lng x xx   ，   2 lnmf x mx xx    ， m R ． （1）求函数  g x 的极值； （2）若    f x g x 在 1, 上为单调函数，求 m 的取值范围； （3）设   2eh x x  ，若在 1,e 上至少存在一个 0x ，使得      0 0 0f x g x h x  成立，求 m 的取值范围． 【答案】（1）   1 ln2g x  极小值 ，无极大值；（2）   ,0 1,   ；（3） 2[ 4 , )1 e e  . 【解析】 【分析】 （1）求得   2 2xg x x   ，即可判断 2x  为函数  g x 的极小值点，问题得解． （2）“    f x g x 在 1, 上为单调函数”可转化为：     ' f x g x   恒大于等于 0 或 者恒小于等于 0，即可转化为： 2 2 0mx x m   或 2 2 0mx x m   在 1, 上恒成立，再 转化为 2 2 1 xm x   在 1, 恒成立或 2 2 1 xm x   在 1, 恒成立，求得  2 2 0,11 x x  ，问题 得解． - 25 - （3）构造函数        F x f x g x h x   ，对 m 的取值分类，当 0m  时，可判断   0F x  恒成立，即 0m  不满足题意，当 0m  时，利用导数可判断  F x 在 1,e 单调递增，结合  min 0F x  ，由题意可得：  max 4 0mF x me e     ，问题得解 【详解】（1）因为   2 2 2 1 2xg x x x x     .由   2 2 2 1 2 0xg x x x x      得: 2x  ， 当 2x  时，   0g x  ，当 0 2x  时，   0g x  所以 2x  为函数  g x 的极小值点    2 1 ln2g x g  极小值 . （2）     2lnmf x g x mx xx     ，     2' 2 2mx x mf x g x x       . 因为    f x g x 在 1, 上为单调函数， 所以 2 2 0mx x m   或 2 2 0mx x m   在 1, 上恒成立， 2 2 0mx x m   等价于 2 2 1 xm x   在 1, 恒成立， 又 2 2 2 2 111 12 x x x xx x      ．当且仅当 1x  时，等号成立 1m  2 2 0mx x m    等价于  21 2m x x  ， 即 2 2 1 xm x   在 1, 恒成立，而  2 2 0,1 , 01 x mx    ． 综上，m 的取值范围是   ,0 1,   ． （3）构造函数         22lnm eF x f x g x h x mx xx x        ， 当 0m  时，   21, , 0, 2ln 0m ex e mx xx x       ， 所以在 1,e 不存在 0x ，使得      0 0 0f x g x h x  当 0m  时，   2 2 2 2 2 2 2 2m e mx x m eF x m x x x x        因为   21, , 2 2 0, 0x e e x mx m      ，所以   0F x  在 1,e 恒成立， - 26 - 故  F x 在 1,e 单调递增， 所以  max 4mF x me e    ，又    min 1 2 0F x F e   所以只需 4 0mme e    ，解之得 2 4 1 em e   ， 故 m 的取值范围是 2[ 4 , )1 e e  . 【点睛】本题主要考查了利用导数求函数的极值，还考查了导数与函数单调性的关系，考查 了构造思想及利用基本不等式求最值，考查了转化思想及计算能力，属于难题．