吉林省长春市普通高中2018届高三质量检测（三）数学（文）试卷+扫描版含答案 9页

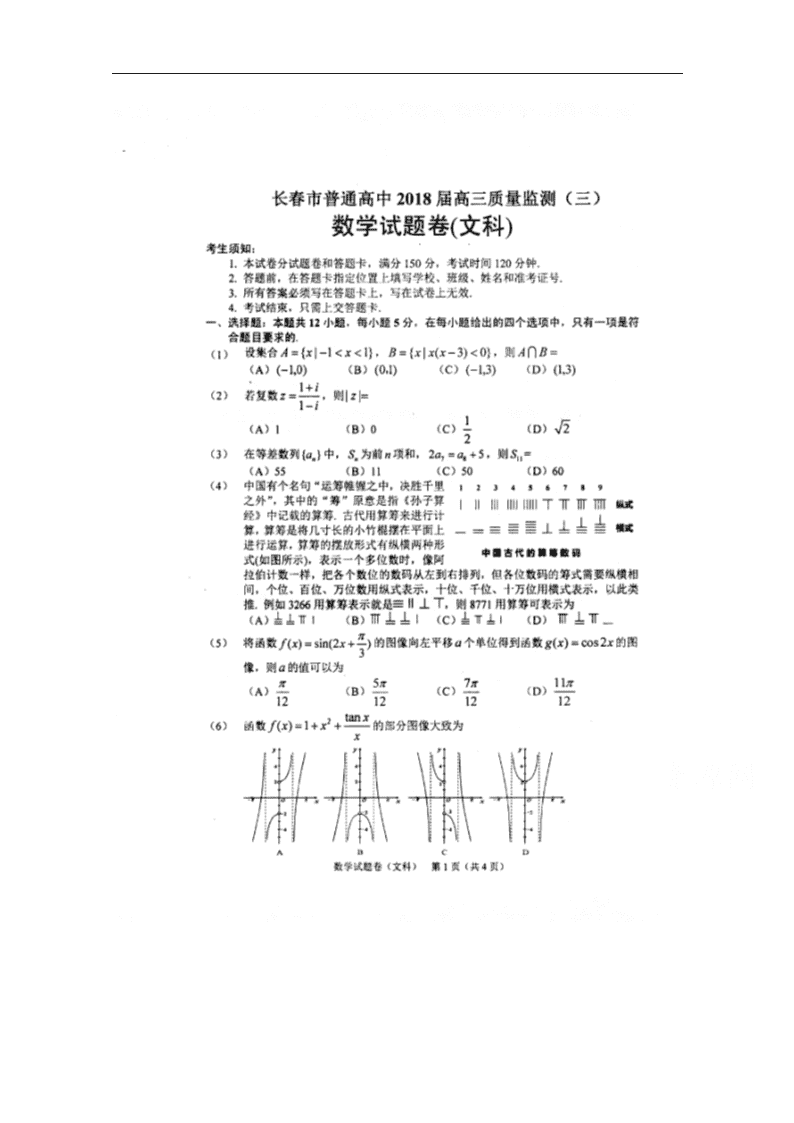
www.ks5u.com www.ks5u.com 长春市普通高中2018届高三质量监测（三）‎ 数学（文科）试题参考答案及评分标准 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1. B 2. A 3. A 4. C 5.A 6. D ‎7. D 8. A 9. B 10. B 11. C 12. B 简答与提示：‎ 1. ‎【命题意图】本题考查集合的运算. ‎ ‎【试题解析】B .故选B. ‎ 2. ‎【命题意图】本题考查复数. ‎ ‎【试题解析】A .故选A. ‎ 3. ‎【命题意图】本题考查等差数列的相关知识. .‎ ‎【试题解析】A　由. 故选A.‎ 4. ‎【命题意图】本题考查中华传统文化中的数学问题.‎ ‎【试题解析】C　由算筹含义. 故选C. ‎ 5. ‎【命题意图】本题考查三角函数的相关知识.‎ ‎【试题解析】A　由题意知，.故选A.‎ 6. 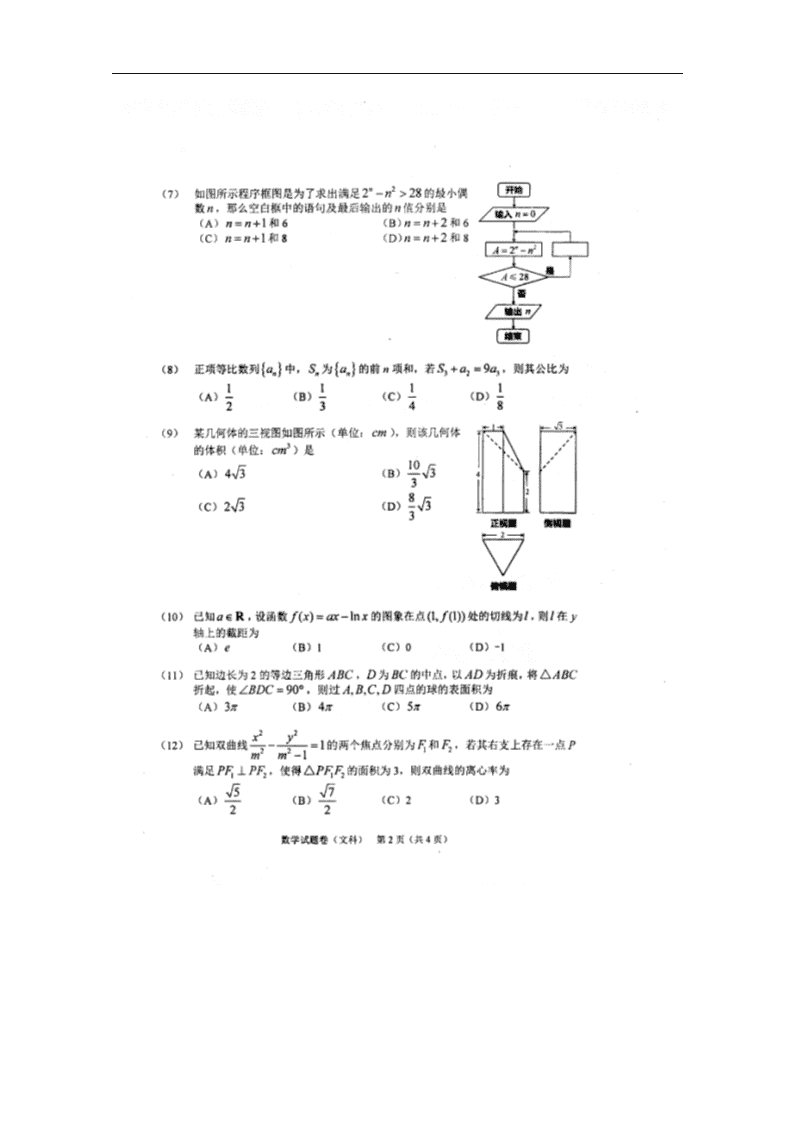‎【命题意图】本题主要考查函数的图象及性质.‎ ‎【试题解析】D 由函数是偶函数，排除A，C，当，.故选D.‎ 7. ‎【命题意图】本题主要考查算法的相关知识. ‎ ‎【试题解析】D　根据程序框图.故选 D.‎ 8. ‎【命题意图】本题考查等比数列的相关知识. ‎ ‎【试题解析】A　由题意可得.故选A. ‎ 9. ‎【命题意图】本题主要考查三视图问题. ‎ ‎【试题解析】B　由题意可知该几何体为正三棱柱去掉一个小三棱锥，.故选B.‎ 10. ‎【命题意图】本题主要考查导数的几何意义. ‎ ‎【试题解析】B 由题意可知，令.故选B. ‎ 11. ‎【命题意图】本题主要考查球的相关问题. ‎ ‎【试题解析】C 折后的图形可放到一个长方体中，其体对角线长为， 故其外接球的半径为，其表面积为.故选C.‎ 12. ‎【命题意图】本题考查双曲线的相关知识. ‎ ‎【试题解析】B　由双曲线可知，从而.故选B.‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13. 14. 15. 16. ‎ 简答与提示：‎ 13. ‎【命题意图】本题考查线性规划问题.‎ ‎【试题解析】由可行域可确定目标函数在处取最大值.‎ 14. ‎【命题意图】本题考查回归方程的相关知识. ‎ ‎【试题解析】将代入回归方程为可得，则，‎ 解得，即精确到0.1后的值约. ‎ 1. ‎【命题意图】本题考查分段函数的相关知识.‎ ‎【试题解析】当，当，故. ‎ 2. ‎【命题意图】本题考查平面向量的相关知识.‎ ‎【试题解析】由题意可知，故. ‎ 三、解答题 17. ‎(本小题满分12分)‎ ‎【命题意图】本题考查解三角形的相关知识. ‎ ‎ 【试题解析】解：（1）由可得 故 ‎ （2）由，由余弦定理可得，‎ ‎ 由基本不等式可得，当且仅当时，“=”成立 从而，故面积的最大值为.‎ 18. ‎(本小题满分12分)‎ ‎ 【命题意图】本小题主要考查学生对频率分布直方图的理解以及分布列的相关知识. ‎ ‎ 【试题解析】解：（1）由，得.‎ ‎ （2）平均数为；岁；‎ 设中位数为，则岁.‎ ‎（3）第1,2,3组的人数分别为20人,30人，从第1,2组中用分层抽样的方法抽取5人，则第1,2组抽取的人数分别为2人,3人，分别记为. ‎ 设从5人中随机抽取3人，为，共10个基本事件，从而第2组中抽到2人的概率.‎ 19. ‎ (本小题满分12分)‎ ‎【命题意图】本小题以四棱锥为载体，考查立体几何的基础知识. 本题考查学生的空间想象能力、推理论证能力和运算求解能力.‎ ‎ 【试题解析】答案：（1）取中点，连接 ‎ 分别是中点, ,‎ ‎ 为中点，为正方形，,‎ ‎ ,四边形为平行四边形 ‎ 平面，平面，平面 ‎ （2）平面,到平面的距离等于到平面的距离,‎ ‎ 平面，, ,在中，‎ ‎ 平面，, , , 平面 ‎ ，,则为直角三角形， ‎ ‎ ,设到平面的距离为，‎ ‎ 则 到平面的距离.‎ 17. ‎(本小题满分12分)‎ ‎【命题意图】本小题考查椭圆的标准方程及直线与椭圆的位置关系，考查学生的逻 辑思维能力和运算求解能力.‎ ‎ 【试题解析】解：（1）设动圆的半径为，由题意知 从而有，故轨迹为以为焦点，长轴长为4的椭圆，并去 除点，从而轨迹的方程为.‎ ‎（2）设的方程为，联立，‎ 消去得，设点，‎ 有有，‎ 点到直线的距离为，点到直线的距离为，‎ 从而四边形的面积 令，有，由函数在单调递增 有，故，四边形面积的最大值为.‎ 18. ‎ (本小题满分12分)‎ ‎【命题意图】本小题主要考查函数与导数的相关知识，以导数为工具研究函数的方法，考查学生解决问题的综合能力.‎ ‎ 【试题解析】解：（1）令，有，当时，，当时，，所以在上单调递减，在上单调递增，在处取得最大值，为，若恒成立，则即.‎ ‎（2）由（1）可知，若函数 有两个零点，则，‎ 要证，只需证，由于在上单调递减，从而只需证，由，，‎ 即证 令，，‎ 有在上单调递增，，所以.‎ 17. ‎ (本小题满分10分)‎ ‎【命题意图】本小题主要考查极坐标系与参数方程的相关知识，本小题考查考生的方程思想与数形结合思想，对运算求解能力有一定要求.‎ ‎ 【试题解析】 （1）联立，，，， 交点坐标 ‎ （2）设,且.，由已知得 ，点的极坐标方程为 18. ‎(本小题满分10分)‎ ‎【命题意图】本小题主要考查不等式的相关知识，具体涉及到绝对值不等式解法等内容. 本小题重点考查化归与转化思想.‎ ‎【试题解析】（1）当m=-2时，‎ ‎ 当解得当恒成立 ‎ 当解得，此不等式的解集为 ‎ ‎ ‎ 当(- ∞，0)时 ‎ 当时，，‎ ‎ 当单调递减，∴f(x)的最小值为3+m ‎ ‎ 设 ‎ 当，当且仅当时，取等号 ‎ 即时，g(x)取得最大值 ‎ ‎ 要使恒成立，只需，即