2020高中数学 第2章 数列 2 4页

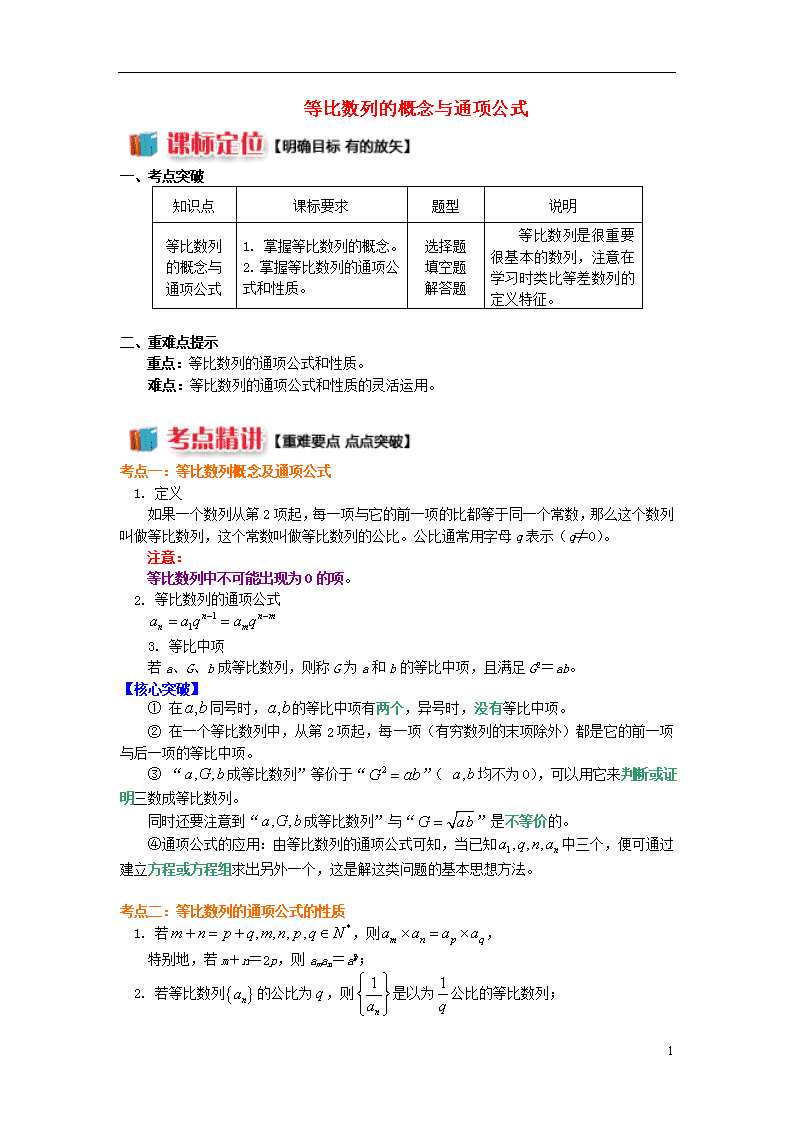
等比数列的概念与通项公式 一、考点突破 知识点 课标要求 题型 说明 等比数列的概念与通项公式 ‎1. 掌握等比数列的概念。‎ ‎2. 掌握等比数列的通项公式和性质。‎ 选择题 填空题 解答题 等比数列是很重要很基本的数列，注意在学习时类比等差数列的定义特征。‎ 二、重难点提示 重点：等比数列的通项公式和性质。‎ 难点：等比数列的通项公式和性质的灵活运用。‎ 考点一：等比数列概念及通项公式 ‎1. 定义 如果一个数列从第2项起，每一项与它的前一项的比都等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比。公比通常用字母q表示（q≠0）。‎ 注意：‎ 等比数列中不可能出现为0的项。‎ ‎2. 等比数列的通项公式 ‎3. 等比中项 若a、G、b成等比数列，则称G为a和b的等比中项，且满足G2＝ab。‎ ‎【核心突破】‎ ‎① 在同号时，的等比中项有两个，异号时，没有等比中项。‎ ‎② 在一个等比数列中，从第2项起，每一项（有穷数列的末项除外）都是它的前一项与后一项的等比中项。‎ ‎③ “成等比数列”等价于“”（ 均不为0），可以用它来判断或证明三数成等比数列。‎ 同时还要注意到“成等比数列”与“”是不等价的。‎ ‎④ 通项公式的应用：由等比数列的通项公式可知，当已知中三个，便可通过建立方程或方程组求出另外一个，这是解这类问题的基本思想方法。‎ 考点二：等比数列的通项公式的性质 ‎1. 若，则，‎ 特别地，若m＋n＝2p，则aman＝a；‎ ‎2. 若等比数列的公比为，则是以为公比的等比数列；‎ 4‎ ‎3. 一组等比数列中，下标成等差数列的项构成等比数列；‎ ‎4. 若与均为等比数列，则也为等比数列；‎ ‎5. 从数列的分类来说：‎ 当，或时，数列为递增数列；‎ 当，或时，数列为递减数列；‎ 当时，数列为常数列；‎ 当时，数列为摆动数列。‎ ‎【要点诠释】‎ 其中性质（1）用得最多，因此我们必须熟记并能灵活运用它，而且它还可以推广。如：若，且，则，也可推广为等式两边含有4项、5项的情形，但不能推广为。‎ 例题1 （等比数列的证明）‎ 已知数列{an}的前n项和Sn＝2n＋1－2，求证{an}是等比数列。‎ 思路分析：由Sn＝2n＋1－2→求an→证明为常数 答案：由Sn＝2n＋1－2，得a1＝S1＝22－2＝2，‎ 当n≥2时，an＝Sn－Sn－1＝2n＋1－2－2n＋2＝2n，‎ 当n＝1时，a1＝2也符合an＝2n，‎ ‎∴an＝2n（n∈N*），‎ ‎∴==2‎ ‎∴{an}是以2为首项，2为公比的等比数列。‎ 技巧点拨：‎ ‎1. 本题已知Sn求an，要利用：‎ 求解。‎ ‎2. 已知通项an证明数列为等比数列的步骤：‎ ‎（1）验证首项a1≠0；‎ ‎（2）证明＝q（q≠0，q为常数）。‎ 例题2 等比数列通项公式的应用）‎ 在等比数列{an}中，‎ ‎（1）若a4＝27，q＝－3，求a7；‎ ‎（2）若a2＝18，a4＝8，求a1与q；‎ ‎（3）若a5－a1＝15，a4－a2＝6，求a3。‎ 思路分析：本题可根据通项公式，列方程或方程组，求出基本量a1和q，再求其他量. ‎ 4‎ 答案：（1）由a4＝a1·q3得a1·（－3）3＝27，‎ ‎∴a1＝－1，‎ ‎∴a7＝a1·q6＝（－1）·（－3）6＝－729。‎ ‎（2）由已知得解得或 ‎（3）由已知得 由得，∴q＝或q＝2。‎ 当q＝时，a1＝－16，a3＝a1q2＝－4；‎ 当q＝2时，a1＝1，a3＝a1q2＝4。‎ 技巧点拨：a1，q是等比数列的基本量，只要求出这两个基本量，其他量便可迎刃而解。求a1，q除上述方法外，也可以充分利用各项之间的关系，先求各项，然后再求q与a1。‎ ‎【综合拓展】‎ 等比数列的综合问题 ‎【满分训练】已知为各项不为1的正项等比数列，满足且，设。‎ ‎（1）数列的前多少项和最大？最大值是多少？‎ ‎（2）是否存在正整数，使当时，恒成立？若存在，求的取值范围；若不存在，则说明理由。‎ 思路分析：（1）根据数列信息，求出数列通项公式，从而解决第一问；‎ ‎（2）由于含参数，注意分类讨论。‎ 答案：（1），且为等比数列，‎ 为等差数列。又 ‎，由，知 故的前12项和最大，其最大值为144。‎ ‎（2）当时，，又，故此时不存在正整数，使。‎ 当时，，又，知，此时只要，则当时，恒有成立。‎ 综上所述，当时，不存在这样的；当时，存在这样的，只要即可。‎ 技巧点拨：对于存在类问题，一般先假设其存在 4‎ ‎，根据题意进行求解或证明，由结果得出结论。另外，在解等差数列与等比数列问题时，关键是抓住它们的相关概念、公式，进行分析、推理、变形。‎ 4‎