【数学】2018届一轮复习北师大版第十章计数原理概率随机变量及其分布第六节离散型随机变量及其分布列教案 11页

第六节　离散型随机变量及其分布列 ‎☆☆☆2017考纲考题考情☆☆☆‎ 考纲要求 真题举例 命题角度 ‎1.理解取有限个值的离散型随机变量及其分布列的概念，了解分布列对于刻画随机现象的重要性；‎ ‎2.理解超几何分布及其导出过程，并能进行简单的应用。‎ ‎2016，天津卷，16,13分(古典概型、分布列、数学期望)‎ ‎2015，重庆卷，18,13分(古典概型、分布列、数学期望)‎ ‎2015，山东卷，18,12分(古典概型、分布列、数学期望)‎ ‎2013，全国卷Ⅰ，19,12分(相互独立事件概率、分布列)‎ ‎　　1.以考查离散型随机变量的分布列及分布列性质的应用为主，常与期望、方差一起考查，另外超几何分布也是考查的热点；‎ ‎2.题型主要是解答题，解题时要求有较强的分析问题、解决问题的能力，要求会依据题设确定离散型随机变量的值及其相应概率。‎ 微知识　小题练 自|主|排|查 ‎1．随机变量的有关概念 如果随机试验的结果可以用一个变量来表示，那么这样的变量叫做随机变量；若变量的所有值可以一一列出，这样的随机变量叫做离散型随机变量。‎ ‎2．离散型随机变量的分布列 ‎(1)概念 若离散型随机变量X可能取的不同值为x1，x2，…，xi，…，xn，X取每一个值xi(i＝1,2,3，…，n)的概率P(X＝xi)＝pi，则称表 X x1‎ x2‎ ‎…‎ xi ‎…‎ xn P p1‎ p2‎ ‎…‎ pi ‎…‎ pn 为离散型随机变量X的概率分布列，简称为X的分布列，有时也用等式P(X＝xi)＝pi，i＝1,2，…，n表示X的分布列。‎ ‎(2)性质 ‎①pi≥0，i＝1,2,3，…，n；‎ ‎②i＝1。‎ ‎3．常见离散型随机变量的分布列 ‎(1)两点分布 X ‎0‎ ‎1‎ P ‎1－p p 若随机变量X的分布列具有上表的形式，就称X服从两点分布，并称p＝P(X＝1)为成功概率。‎ ‎(2)超几何分布 在含有M件次品的N件产品中，任取n件，其中恰有X件次品，则P(X＝k)＝，k＝0,1,2，…，m，其中m＝min{M，n}，且n≤N，M≤N，n，M，N∈N*。‎ X ‎0‎ ‎1‎ ‎…‎ m P ‎…‎ 如果随机变量X的分布列具有上表的形式，则称随机变量X服从超几何分布。‎ 微点提醒 ‎1．某一变量为离散型随机变量满足的条件：(1)随着试验结果变化而变化；(2)所有取值可以一一列出。‎ ‎2．离散型随机变量的分布列指出了随机变量X的取值范围以及取各个值的概率。在求离散型随机变量的分布列时，可以用它的两条性质检验分布列的正误：一是pi≥0(i＝1,2，…)；二是p1＋p2＋…＋pn＝1。‎ 小|题|快|练 一 、走进教材 ‎1．(选修2－3P‎68A组T2改编)设随机变量X的概率分布列为 X ‎1‎ ‎2‎ ‎3‎ ‎4‎ P m 则P(|X－3|＝1)＝(　　)‎ A. B. C. D. 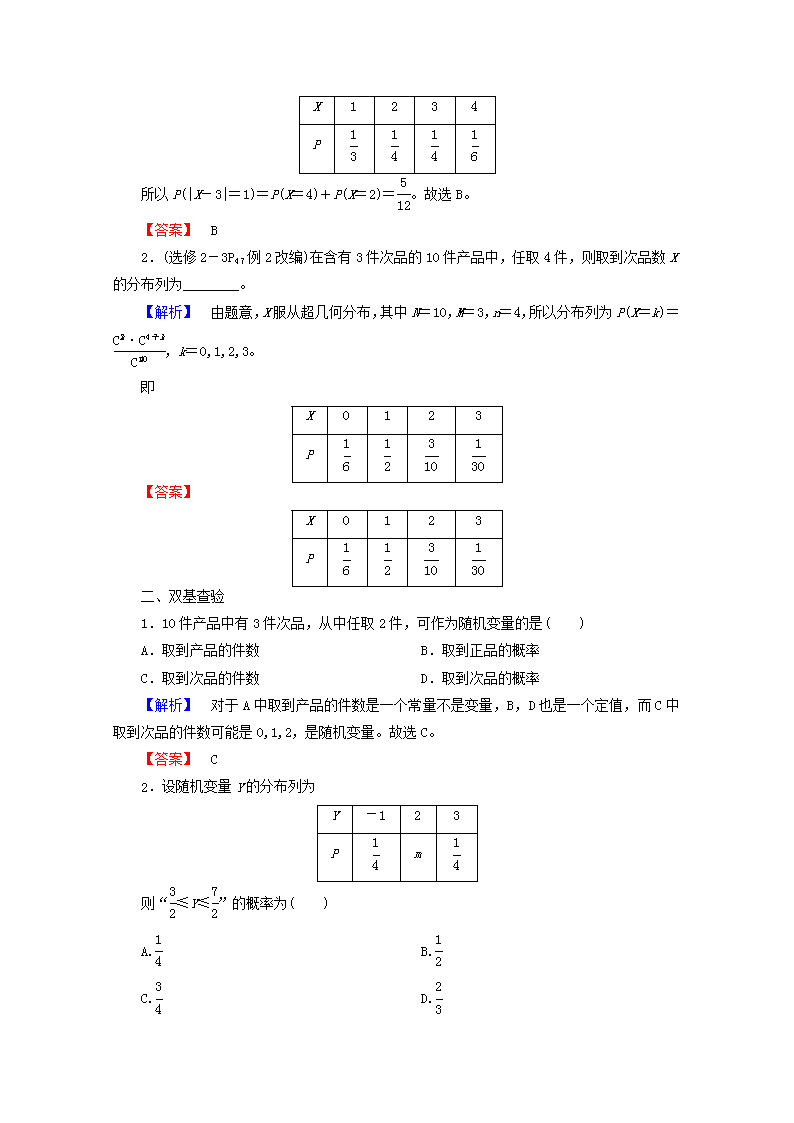‎【解析】　根据概率分布的定义得出：＋m＋＋＝1，得m＝，随机变量X的概率分布列为 X ‎1‎ ‎2‎ ‎3‎ ‎4‎ P 所以P(|X－3|＝1)＝P(X＝4)＋P(X＝2)＝。故选B。‎ ‎【答案】　B ‎2．(选修2－3P47例2改编)在含有3件次品的10件产品中，任取4件，则取到次品数X的分布列为________。‎ ‎【解析】　由题意，X服从超几何分布，其中N＝10，M＝3，n＝4，所以分布列为P(X＝k)＝，k＝0,1,2,3。‎ 即 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎【答案】　‎ X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 二、双基查验 ‎1．10件产品中有3件次品，从中任取2件，可作为随机变量的是(　　)‎ A．取到产品的件数　　　 B．取到正品的概率 C．取到次品的件数 D．取到次品的概率 ‎【解析】　对于A中取到产品的件数是一个常量不是变量，B，D也是一个定值，而C中取到次品的件数可能是0,1,2，是随机变量。故选C。‎ ‎【答案】　C ‎2．设随机变量Y的分布列为 Y ‎－1‎ ‎2‎ ‎3‎ P m 则“≤Y≤”的概率为(　　)‎ A. B. C. D. ‎【解析】　因为＋m＋＝1，所以m＝，‎ 所以P＝P(2)＋P(3)＝。‎ ‎【答案】　C ‎3．从1,2,3,4四个数字中任取两个数，两数之和为X，则P(X＝5)＝________。‎ ‎【解析】　从1,2,3,4四个数字中任取两个数，共有6种选法，基本事件空间Ω＝{(1,2)，(1,3)，(1,4)，(2,3)，(2,4)，(3,4)}，‎ X＝3,4,5,6,7，‎ 所以P(X＝5)＝＝。‎ ‎【答案】　 ‎4．从装有3个红球，2个白球的袋中随机取出2个球，设其中有X个红球，则随机变量X的概率分布为 X ‎0‎ ‎1‎ ‎2‎ P ‎【解析】　P(X＝0)＝＝0.1，P(X＝1)＝＝0.6，P(X＝2)＝＝0.3。‎ ‎【答案】　0.1　0.6　0.3‎ 微考点　大课堂 考点一 ‎ 随机变量的概念 ‎【典例1】　写出下列随机变量可能的取值，并说明随机变量所表示的意义。‎ ‎(1)一个袋中装有2个白球和5个黑球，从中任取3个，其中所含白球的个数X；‎ ‎(2)投掷两枚骰子，所得点数之和为X，所得点数的最大值为Y。‎ ‎【解析】　(1)X可取0,1,2。‎ X＝0表示所取的三个球没有白球；‎ X＝1表示所取的三个球是1个白球，2个黑球；‎ X＝2表示所取的三个球是2个白球，1个黑球。‎ ‎(2)X的可能取值有2,3，…，12，Y的可能取值为1,2,3，…，6。若以(i，j)表示先后投掷的两枚骰子出现的点数，则 X＝2表示(1,1)；‎ X＝3表示(1,2)，(2,1)；‎ X＝4表示(1,3)，(2,2)，(3,1)；‎ ‎…‎ X＝12表示(6,6)。‎ Y＝1表示(1,1)；‎ Y＝2表示(1,2)，(2,1)，(2,2)；‎ Y＝3表示(1,3)，(2,3)，(3,3)，(3,1)，(3,2)；‎ ‎…‎ Y＝6表示(1,6)，(2,6)，(3,6)，…，(6,6)，(6,5)，…，(6,1)。‎ 反思归纳　所谓的随机变量就是试验结果和实数之间的一个对应关系，随机变量是将试验的结果数量化，变量的取值对应随机试验的某一个随机事件。写随机变量表示的结果，要看三个特征：①可用数来表示；②试验之前可以判断其可能出现的所有值；③在试验之前不能确定值。‎ ‎【变式训练】　某校为学生定做校服，规定凡身高不超过‎160 cm的学生交校服费80元。凡身高超过‎160 cm的学生，身高每超过‎1 cm多交3元钱(不足‎1 cm时按‎1 cm计)。若学生应交的校服费为η，学生身高用ξ表示，则η和ξ是否为离散型随机变量？‎ ‎【解析】　由于该校的每一个学生对应着唯一的身高，并且ξ取整数值(不足‎1 cm按‎1 cm计)，因此ξ是一个离散型随机变量。而η＝ 所以η也是一个离散型随机变量。‎ ‎【答案】　是离散型随机变量 考点二 ‎ 随机变量的性质 ‎【典例2】　(1)设X是一个离散型随机变量，其分布列为：‎ X ‎－1‎ ‎0‎ ‎1‎ P ‎1－2q q2‎ 则q等于(　　)‎ A．1　　　　　　　　　 B．1± C．1－ D．1＋ ‎(2)设离散型随机变量X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎0.2‎ ‎0.1‎ ‎0.1‎ ‎0.3‎ m 求|X－1|的分布列。‎ ‎【解析】　(1)由分布列的性质知 所以q＝1－。‎ ‎(2)由分布列的性质，‎ 知0.2＋0.1＋0.1＋0.3＋m＝1，∴m＝0.3。‎ 列表 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ η＝|X－1|‎ ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎∴P(η＝1)＝P(X＝0)＋P(X＝2)＝0.2＋0.1＝0.3，‎ P(η＝0)＝P(X＝1)＝0.1，P(η＝2)＝P(X＝3)＝0.3，P(η＝3)＝P(X＝4)＝0.3。‎ 因此η＝|X－1|的分布列为：‎ η ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎0.1‎ ‎0.3‎ ‎0.3‎ ‎0.3‎ ‎【答案】　(1)C　(2)见解析 反思归纳　利用分布列中各概率之和为1可求参数的值，此时要注意检验，以保证每个概率值均为非负数。‎ ‎【变式训练】　随机变量X的分布列如下：‎ X ‎－1‎ ‎0‎ ‎1‎ P a b c 其中a，b，c成等差数列，则P(|X|＝1)＝______。‎ ‎【解析】　由题意知 则2b＝1－b，则b＝，a＋c＝，‎ 所以P(|X|＝1)＝P(X＝－1)＋P(X＝1)＝a＋c＝。‎ ‎【答案】　 考点三 ‎ 求离散型随机变量的分布列 ‎【典例3】　(2016·天津高考)某小组共10人，利用假期参加义工活动。已知参加义工活动次数为1,2,3的人数分别为3,3,4。现从这10人中随机选出2人作为该组代表参加座谈会。‎ ‎(1)设A为事件“选出的2人参加义工活动次数之和为‎4”‎，求事件A发生的概率；‎ ‎(2)设X为选出的2人参加义工活动次数之差的绝对值，求随机变量X的分布列和数学期望。‎ ‎【解析】　(1)由已知，有P(A)＝＝。‎ 所以，事件A发生的概率为。‎ ‎(2)随机变量X的所有可能取值为0,1,2。‎ P(X＝0)＝＝，‎ P(X＝1)＝＝，‎ P(X＝2)＝＝。‎ 所以，随机变量X的分布列为 X ‎0‎ ‎1‎ ‎2‎ P 随机变量X的数学期望E(X)＝0×＋1×＋2×＝1。‎ ‎【答案】　(1)　(2)见解析 反思归纳　求离散型随机变量X的分布列的步骤：①理解X的意义，写出X可能取的全部值；②求X取每个值的概率；③写出X的分布列。‎ 求离散型随机变量的分布列的关键是求随机变量所取值对应的概率，在求解时，要注意应用计数原理、古典概型等知识。‎ ‎【变式训练】　(2016·广西质检)某技术公司新开发了A，B两种新产品，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品，现随机抽取这两种产品各100件进行检测，检测结果统计如下：‎ 测试指标 ‎[70,76)‎ ‎[76,82)‎ ‎[82,88)‎ ‎[88,94)‎ ‎[94,100]‎ 产品A ‎8‎ ‎12‎ ‎40‎ ‎32‎ ‎8‎ 产品B ‎7‎ ‎18‎ ‎40‎ ‎29‎ ‎6‎ ‎(1)试分别估计产品A、产品B为正品的概率；‎ ‎(2)生产一件产品A，若是正品可盈利80元，次品则亏损10元；生产一件产品B，若是正品可盈利100元，次品则亏损20元，在(1)的前提下，记X为生产一件产品A和一件产品B所得的总利润，求随机变量X的分布列。‎ ‎【解析】　(1)产品A为正品的概率约为＝。‎ 产品B为正品的概率约为＝。‎ ‎(2)随机变量X的所有取值为180,90,60，－30。‎ P(X＝180)＝×＝；‎ P(X＝90)＝×＝；‎ P(X＝60)＝×＝；‎ P(X＝－30)＝×＝。‎ 所以随机变量X的分布列为：‎ X ‎180‎ ‎90‎ ‎60‎ ‎－30‎ P ‎【答案】　(1)产品A、B为正品概率分别为， ‎(2)见解析 考点四 ‎ 超几何分布母题发散 ‎【典例4】　(2015·重庆高考改编)端午节吃粽子是我国的传统习俗。设一盘中装有10个粽子，其中豆沙粽2个，肉粽3个，白粽5个，这三种粽子的外观完全相同。从中任意选取3个。‎ ‎(1)求三种粽子各取到1个的概率；‎ ‎(2)设X表示取到的豆沙粽个数，求X的分布列。‎ ‎【解析】　(1)令A表示事件“三种粽子各取到1个”，则由古典概型的概率计算公式有P(A)＝＝。‎ ‎(2)X的所有可能值为0,1,2，且 P(X＝0)＝＝，P(X＝1)＝＝，‎ P(X＝2)＝＝。‎ 综上知，X的分布列为 X ‎0‎ ‎1‎ ‎2‎ P ‎【答案】　(1)　(2)见解析 ‎【母题变式】　若本典例中的X表示取到的粽子的种类，求X的分布列。‎ ‎【解析】　由题意知X的所有可能值为1,2,3，且 P(X＝1)＝＝＝，‎ P(X＝3)＝＝＝，‎ P(X＝2)＝1－P(X＝1)－P(X＝3)＝1－－＝。‎ 综上可知，X的分布列为 X ‎1‎ ‎2‎ ‎3‎ P 反思归纳　超几何分布描述的是不放回抽样问题，随机变量为抽到的某类个体的个数。超几何分布的特征是：(1)考察对象分两类；(2)已知各类对象的个数；(3)从中抽取若干个个体，考查某类个体数X的概率分布。超几何分布主要用于抽检产品、摸不同类别的小球等概率模型，其实质是古典概型。‎ ‎【拓展变式】　(2017·衡水模拟)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的可入肺颗粒物。根据现行国家标准，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标。‎ 从某自然保护区某年全年每天的PM2.5监测数据中随机地抽取10天的数据作为样本，监测值频数如下表所示：‎ PM2.5日均值(微克/立方米)‎ ‎[25,35)‎ ‎[35,45)‎ ‎[45,55)‎ ‎[55,65)‎ ‎[65,75)‎ ‎[75,85]‎ 频数 ‎3‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎3‎ ‎(1)从这10天的PM2.5日均值监测数据中，随机抽取3天，求恰有一天空气质量达到一级的概率。‎ ‎(2)从这10天的数据中任取3天数据，记ξ表示抽到PM2.5监测数据超标的天数，求ξ的分布列。‎ ‎【解析】　(1)记“10天的PM2.5日均值监测数据中，随机抽出3天，恰有一天空气质量达到一级”为事件A，则P(A)＝＝。‎ ‎(2)依据条件，ξ服从超几何分布，其中N＝10，M＝3，n＝3，且随机变量ξ可能取值为0,1,2,3。‎ P(ξ＝k)＝(k＝0,1,2,3)，‎ 所以P(ξ＝0)＝＝，P(ξ＝1)＝＝，‎ P(ξ＝2)＝＝，P(ξ＝3)＝＝。‎ 因此ξ的分布列为 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎【答案】　(1)　(2)见解析 微考场　新提升 ‎1．(2017·郑州模拟)已知随机变量X的分布列为P(X＝i)＝(i＝1,2,3,4)，则P(2＜X≤4)等于(　　)‎ A. B. C. D. 解析　由分布列的性质得＋＋＋＝1，则a＝5。所以，P(2＜X≤4)＝P(X＝3)＋P(X＝4)＝＋＝。‎ 答案　B ‎2．某射手射击所得环数X的分布列为 X ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ P ‎0.02‎ ‎0.04‎ ‎0.06‎ ‎0.09‎ ‎0.28‎ ‎0.29‎ ‎0.22‎ 则此射手“射击一次命中环数大于‎7”‎的概率为(　　)‎ A．0.28 B．0.88‎ C．0.79 D．0.51‎ 解析　P(X＞7)＝P(X＝8)＋P(X＝9)＋P(X＝10)＝0.28＋0.29＋0.22＝0.79。‎ 答案　C ‎3．(2016·邢台模拟)袋中装有编号为1的球5个，编号为2的球3个，这些球的大小完全一样。‎ ‎(1)从中任意取出四个，求剩下的四个球都是1号球的概率。‎ ‎(2)从中任意取出三个，记ξ为这三个球的编号之和，求随机变量ξ的分布列。‎ 解析　(1)记“任意取出四个，剩下的四个球都是1号球”为事件A，则P(A)＝＝。‎ ‎(2)ξ的可能取值为3,4,5,6，则P(ξ＝3)＝＝＝，P(ξ＝4)＝＝＝。‎ P(ξ＝5)＝＝，P(ξ＝6)＝＝。‎ 概率分布列如下：‎ ξ ‎3‎ ‎4‎ ‎5‎ ‎6‎ P 答案　　(2)见解析 ‎4．某超市在节日期间进行有奖促销，凡在该超市购物满300元的顾客，将获得一次摸奖机会，规则如下：‎ 奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球。顾客不放回地每次摸出1个球，若摸到黑球则停止摸奖，否则就要将奖盒中的球全部摸出才停止。规定摸到红球奖励10元，摸到白球或黄球奖励5元，摸到黑球不奖励。‎ ‎(1)求1名顾客摸球3次停止摸奖的概率；‎ ‎(2)记X为1名顾客摸奖获得的奖金数额，求随机变量X的分布列。‎ 解析　(1)设“1名顾客摸球3次停止摸奖”为事件A，‎ 则P(A)＝＝，‎ 故1名顾客摸球3次停止摸球的概率为。‎ ‎(2)随机变量X的所有取值为0,5,10,15,20。‎ P(X＝0)＝，P(X＝5)＝＝，‎ P(X＝10)＝＋＝，‎ P(X＝15)＝＝，‎ P(X＝20)＝＝。‎ 所以，随机变量X的分布列为 X ‎0‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ P 答案　(1)　(2)见解析