2020届河南省郑州市高三上学期第一次质量预测数学（理）试题 11页

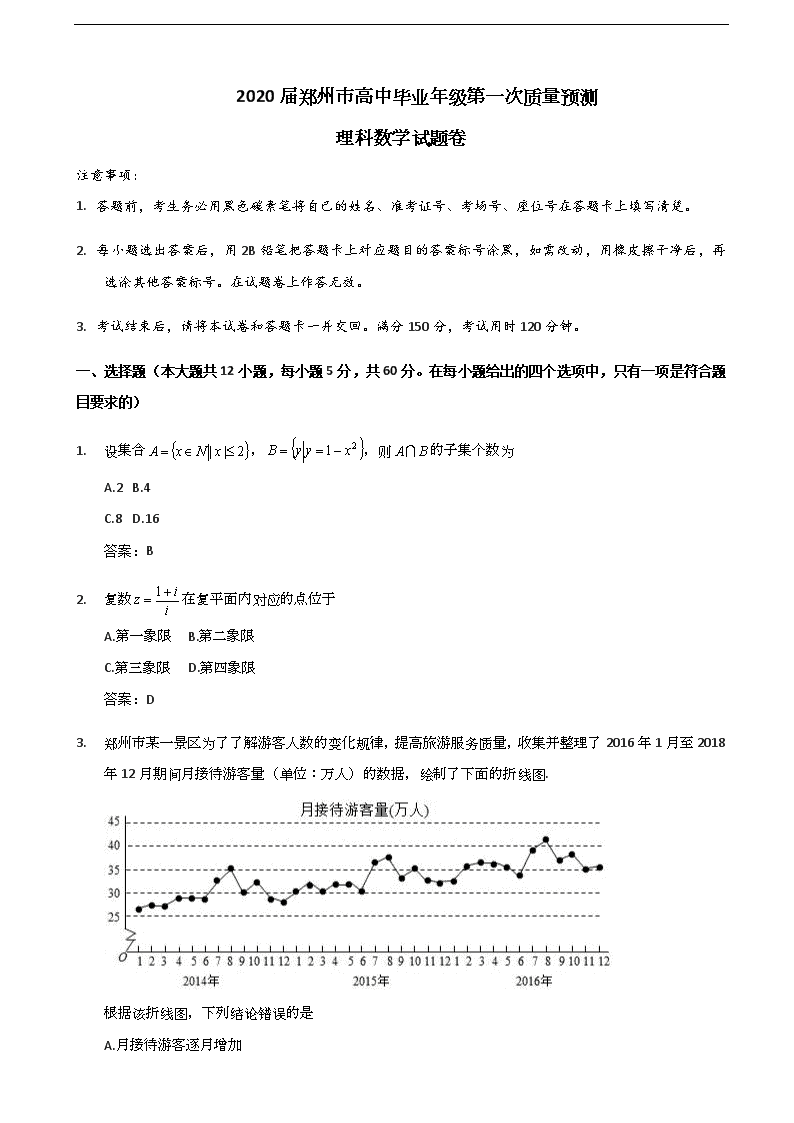
‎2020届郑州市高中毕业年级第一次质量预测 理科数学试题卷 注意事项：‎ 1. 答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。‎ 2. 每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。在试题卷上作答无效。‎ 3. 考试结束后，请将本试卷和答题卡一并交回。满分150分，考试用时120分钟。‎ 一、 选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ 1. 设集合，，则的子集个数为 A.2 B.4 C.8 D.16 答案：B 2. 复数在复平面内对应的点位于 A.第一象限 B.第二象限 C.第三象限 D.第四象限 答案：D 3. 郑州市某一景区为了了解游客人数的变化规律，提高旅游服务质量，收集并整理了2016年1月至2018年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图. ‎ ‎ 根据该折线图，下列结论错误的是 A.月接待游客逐月增加 B.年接持游客量逐年增加 C.各年的月接待游客量高峰期大致在7，8月 D.各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳 答案：A 1. 定义在R上的函数为偶函數，，，，则 A. B. C. D. 答案：C 2. ‎“纹样”是中国艺术宝库的瑰宝，“火纹”是常见的一种传统纹样，为了测算某火纹纹样（如图阴影部分所示）的面积，作一个边长为3的正方形将其包含在内，并向该正方形内随机投掷2000个点，己知恰有800个点落在阴影部分，据此可估计阴影部分的面积是 A. B. C. D. 答案：B 3. 已知向量与夹角为，且，，则 A. B. C. D. 答案：C 4. 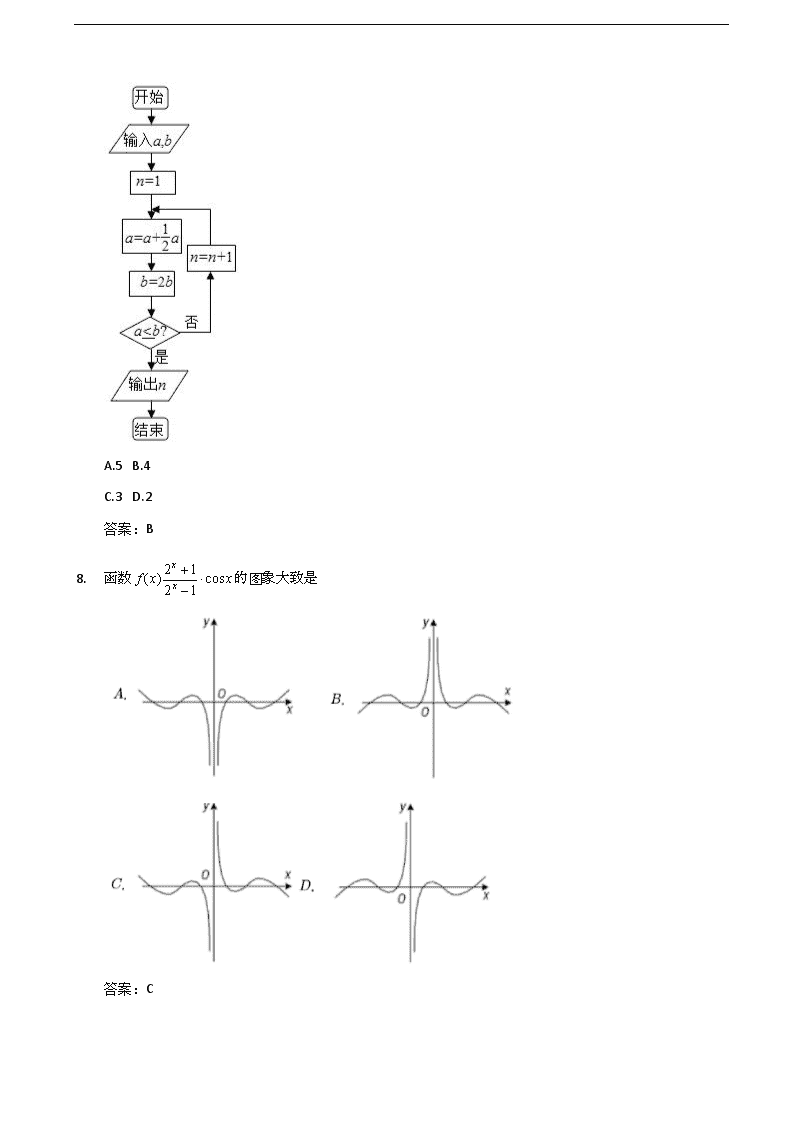宋元时期数学名著《算学启蒙》中有关于“松竹并生"的问题，松长三尺，竹长一尺，松日自半，竹日自倍，松竹何日而长等，如图是源于其思想的一个程序框图，若输人的，分别为3，1，则输出的等于 ‎ ‎ А.5 B.4 C.3 D.2 答案：B 1. 函数的图象大致是 答案：C 1. 第十一届全国少数民族传统体育运动会在河南郑州举行，某项目比赛期间需要安排3名志愿者完成5项工作，每人至少完成一项，每项工作由一人完成，则不同的安排方式共有多少种 A.60 B.90 C.120 D.150 答案：D 2. 已知抛物线的焦点为，准线为，是上一点，直线与抛物线交于，两点，若，则= A. B. C. D. 答案：B 3. 已知三棱锥内接于球O，平面ABC，为等边三角形，且边长为，球的表面积为，则直线PC与平面PAB所成的角的正弦值为 A. B. C. D. 答案：D 4. ‎,，若有9个零点，则的取值范围是 A. B. C. D. 答案：A 二、填空题：本大题共4小题，每小题5分，共20分.‎ 5. 曲线在点处的切线方程为___________. 答案：‎ 6. 若是等差数列的前项和，若，，则___________. 答案：‎ 1. 已知双曲线的右顶点为A，以A为圆心，6为半径做圆，圆A与双曲线C的一条渐近线相交于M，N两点，若（为坐标原点），则双曲线C的离心率为___________. 答案：‎ 2. 已知数列满足：对任意均有（p为常数，且），若，则的所有可能取值的集合是___________. 答案：‎ 三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤，第17~21题为必考题，每个试题考生都必须作答，第22，23题为选考题，考生根据要求作答.‎ ‎（一）必考题：共60分 3. ‎（12分） 已知ABC外接圆半径为R，其内角A，B，C的对边长分别为a，b，c，设. （1）求角B； （Ⅱ）若b=12，c=8，求sinA的值 【解析】(I) ∴ 即： ……3分 ∴ 因为所以……6分 (II)若，由正弦定理，, , 由，故为锐角，……9分……12分 1. ‎（12分） 已知三棱锥M-ABC中，MA=MB=MC=AC=，AB=BC=2，O为AC的中点，点N在校BC上，且. （1）证明：BO平面AMC； （2）求二面角N-AM-C的正弦值. 【解析】（I）如图所示：连接， 在中：，则，.2分 在中：，为的中点，则，且 ……4分 在中：，满足： 根据勾股定理逆定理得到 相交于 ， 故平面………………….6分 （Ⅱ）因为两两垂直，建立空间直角坐标系如图所示． 因为, 则……8分 由所以， 设平面的法向量为，则 令，得……10分 因为平面，所以为平面的法向量， 所以与 所成角的余弦为． 所以二面角的正弦值为.……12分 1. ‎（12分） 已知椭圆的离心率为，且过点. （1）求椭圆E的方程； （2）若过点的任意直线与椭圆E相交于A，B两点，线段AB的中点为M，求证，恒有. 【解析】（I）由题意知，.……1分 又因为解得，. ……3分 所以椭圆方程为. ……4分 （Ⅱ） 设过点直线为，设， 由得，且. 则 又因为，， ，……10分 所以. 因为线段的中点为，所以.……12分 2. ‎（12） 水污染现状与工业废水排放密切相关，某工厂深人贯彻科学发展观，努力提高污水收集处理水平，其污水处理程序如下：原始污水必先经过A系统处理，处理后的污水（A级水）达到环保标准（简称达标）的概率为p（0