【数学】2018届一轮复习北师大版三角函数的性质学案 6页

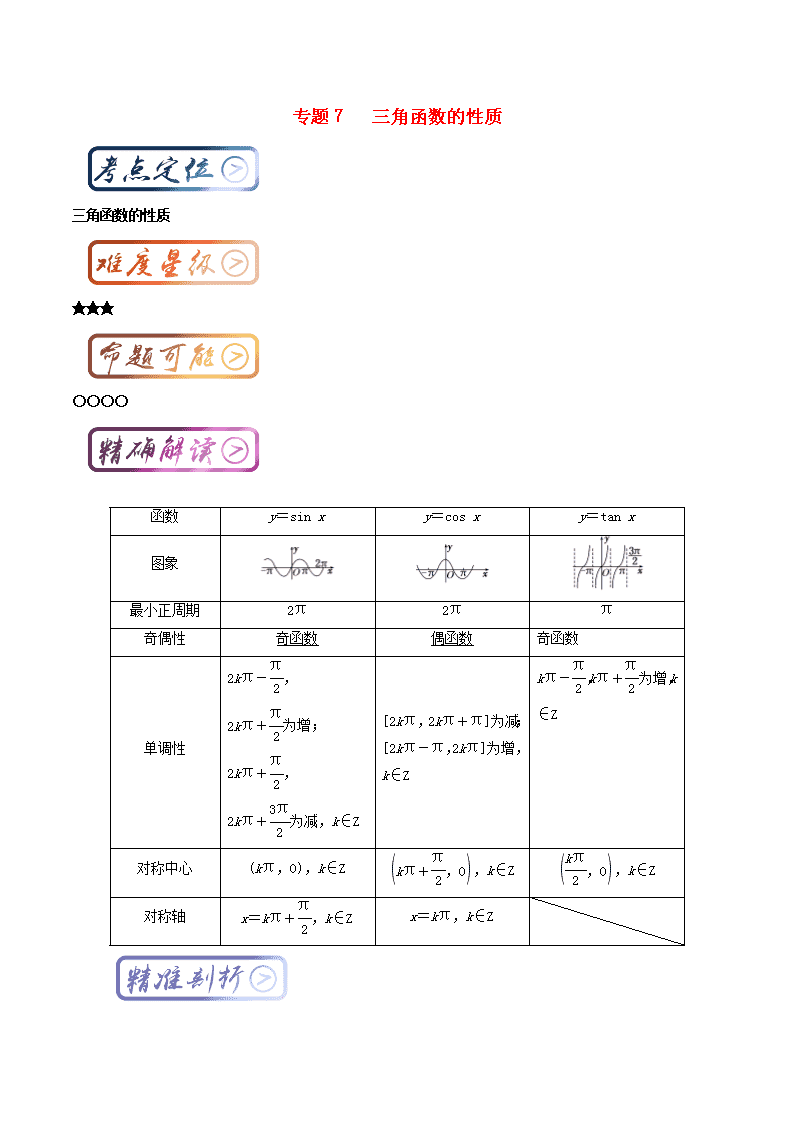
专题7 三角函数的性质 三角函数的性质 ‎★★★‎ ‎○○○○‎ 函数 y＝sin x y＝cos x y＝tan x 图象 最小正周期 ‎2π ‎2π π 奇偶性 奇函数 偶函数 奇函数 ‎ 单调性 ‎2kπ－，‎ ‎2kπ＋为增；‎ ‎2kπ＋，‎ ‎2kπ＋为减，k∈Z ‎[2kπ，2kπ＋π]为减；[2kπ－π，2kπ]为增，k∈Z kπ－，kπ＋为增，k∈Z 对称中心 ‎(kπ，0)，k∈Z ，k∈Z ，k∈Z 对称轴 x＝kπ＋，k∈Z x＝kπ，k∈Z 求三角函数单调区间的两种方法 ‎(1)代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个角u(或t)，利用基本三角函数的单调性列不等式求解．‎ ‎(2)图象法：画出三角函数的正、余弦曲线，结合图象求它的单调区间．‎ ‎[提醒]　求解三角函数的单调区间时，若x的系数为负，应先化为正，同时切莫忽视函数自身的定义域．‎ ‎[例1]　求下列函数的单调区间：‎ ‎(1)f(x)＝sin，x∈[0，π]；‎ ‎(2)f(x)＝|tan x|；‎ ‎(3)f(x)＝cos，x∈.‎ ‎ ‎ ‎(2)观察图象可知，y＝|tan x|的单调递增区间是，k∈Z，单调递减区间是kπ－，kπ，k∈Z.‎ ‎(3)当2kπ－π≤2x－≤2kπ(k∈Z)，‎ 即kπ－≤x≤kπ＋，k∈Z时，函数f(x)是增函数；‎ 当2kπ≤2x－≤2kπ＋π(k∈Z)，即kπ＋≤x≤kπ＋，k∈Z时，函数f(x)是减函数．‎ 因此函数f(x)在上的单调递增区间是－，，单调递减区间为，.‎ ‎[例2]　已知ω>0，函数f(x)＝sin在上是减函数，则ω的取值范围是________．‎ ‎[解析]　由＜x＜π，得ω＋＜ωx＋＜πω＋，由题意知⊆＋2kπ，＋2kπ(k∈Z)且≥2×，则 且0＜ω≤2，故≤ω≤.‎ ‎[答案]　 ‎[例3]　(1)函数y＝1－2sin2是(　　)‎ A．最小正周期为π的奇函数 B．最小正周期为π的偶函数 C．最小正周期为的奇函数 D．最小正周期为的偶函数 ‎(2)若函数f(x)＝2tan的最小正周期T满足1＜T＜2，则自然数k的值为________．‎ ‎[解析]　(1)y＝1－2sin2＝cos 2x－＝－sin 2x，‎ 所以f(x)是最小正周期为π的奇函数．‎ ‎(2)由题意知，1＜＜2，‎ 即|k|＜π＜2|k|.又k∈N，‎ 所以k＝2或k＝3.‎ ‎[答案]　(1)A　(2)2或3‎ ‎[例4]　(1)函数f(x)＝(1＋cos 2x)sin2x(x∈R)是(　　)‎ A．最小正周期为π的奇函数 B．最小正周期为的奇函数 C．最小正周期为π的偶函数 D．最小正周期为的偶函数 ‎(2)若函数f(x)＝sin(φ∈[0,2π])是偶函数，则φ＝(　　)‎ A. B. ‎ C. D. ‎ ‎ ‎[答案]　(1)D　(2)C ‎1.函数y＝3cos的最小正周期是(　　)‎ A.　　　　　　　　　　　 B. C．2π D．5π 解析：选D　由T＝＝5π，知该函数的最小正周期为5π.‎ ‎2.已知函数f(x)＝Acos(ωx＋φ)(A>0，ω>0，φ∈R)，则“f(x)是奇函数”是“φ＝”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 解析：选B　f(x)是奇函数时，φ＝＋kπ(k∈Z)，充分性不成立；φ＝时，f(x)＝Acos＝－Asin ωx，为奇函数，必要性成立．所以“f(x)是奇函数”是“φ＝”的必要不充分条件．‎ ‎3.若函数y＝cos(ω∈N*)图象的一个对称中心是，则ω的最小值为(　　)‎ A．1 B．‎2 C．4 D．8‎ 解析：选B　由题可知，＋＝kπ＋(k∈Z)，所以ω＝6k＋2(k∈Z)．又ω∈N*，则ωmin＝2.‎ ‎4.已知函数f(x)＝2sin(2x＋φ)在区间上单调且最大值不大于，则φ的取值范围是(　　)‎ A. B. C. D. ‎5.(2017·武汉调研)已知函数f(x)＝sin(x∈R)，下列结论错误的是(　　)‎ A．函数f(x)是偶函数 B．函数f(x)的最小正周期为π C．函数f(x)在区间上是增函数 D．函数f(x)的图象关于直线x＝对称 解析：选D　f(x)＝sin＝－cos 2x，此函数为最小正周期为π的偶函数，所以A，B正确．由函数y＝cos x的单调性知C正确．函数图象的对称轴方程为x＝(k∈Z)，显然，无论k取任何整数，x≠，所以D错误．‎ ‎6.已知函数f(x)＝2sin(ωx＋φ)，对于任意x都有f＝f，则f的值为________．‎ 解析：∵f＝f，∴x＝是函数f(x)＝2sin(ωx＋φ)的一条对称轴．∴f＝±2.‎ 答案：2或－2‎ ‎7.函数y＝2sin(x∈[0，π])为增函数的区间是________．‎ 答案： ‎________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________‎