2015漳州1月份质检理数（八校联考）试卷 14页

www.ks5u.com ‎2014—2015学年漳州八校高三第一次联考理科数学试题 ‎（考试时间：120分钟 总分：150分）‎ 命题人：程溪中学 许飘勇 审核人：王友祥 第Ⅰ卷（选择题 共50分）‎ 一、选择题:（本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的）.‎ ‎1．复数等于 ‎ A． B． C．－1+i D．－1－i ‎2．命题“对任意的”的否定是 A．　不存在 B．　存在 C．　存在 D．　对任意的 ‎3.右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是 A． 　　　　　　　　　　 　B． ‎ C． 　　　　　　　　　　　 D．‎ ‎4.设若的最小值为 (　)‎ ‎ A 8 B ‎4 C 1 D ‎ ‎5.如果执行右面的框图，输入，则输出的数等于(　　)‎ A B C D ‎ ‎6.若m、n为两条不同的直线，α、β为两个不同的平面，则以下命题 正确的是(　　)‎ ‎ A．若m∥α，nα，则m∥n B．若m∥α，mβ，α∩β=n，则m∥n C．若m∥α，n∥α，则m∥n D．若α∩β =m，m⊥n，则n⊥α ‎7. 如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为(　　) ‎ A B C D ‎8．为得到函数的图象，只需将函数的图象(　　)‎ A．向左平移个长度单位 B．向右平移个长度单位 C．向左平移个长度单位 D．向右平移个长度单位 ‎9.设变量x，y满足约束条件：.则目标函数z=2x+3y的最小值为(　　)‎ A 6 B 7 C 8 D 23‎ ‎10.设非空集合满足：当时，有。给出如下三个命题工：①若，则；②若，则；③若，则。其中正确命题的个数是(　　)‎ ‎ A.0 B.1 C.2 D.3‎ 第Ⅱ卷(非选择题 共100分)‎ 二、填空题：（本大题共5小题，每小题4分，共20分. 把答案填在答题卷中的横线上）.‎ ‎11.设向量a＝(cosθ，1)，b＝(1,3cosθ)，且a∥b，则cos2θ＝________.‎ ‎12.的展开式的常数项是 （用数字作答） ‎ ‎13．如右图，一矩形铁皮的长为8cm，宽为5cm，在四个角上截去四个相同的小正方形，制成一个无盖的小盒子，问小正方形的边长为_________ cm时，小盒子容积最大。 ‎ ‎14．已知函数，，，实数是函数的一个零点．给出下列四个判断：①；②；③；④．其中可能成立的是____________（填序号）‎ ‎15．设△ABC的三边长分别为a，b，c，△ABC的面积为S，则△ABC的内切圆半径为r＝.将此结论类比到空间四面体：设四面体S－ABC的四个面的面积分别为S1，S2，S3，S4，体积为V，则四面体的内切球半径为r＝________.‎ 三、解答题：（本大题共6小题，共80分. 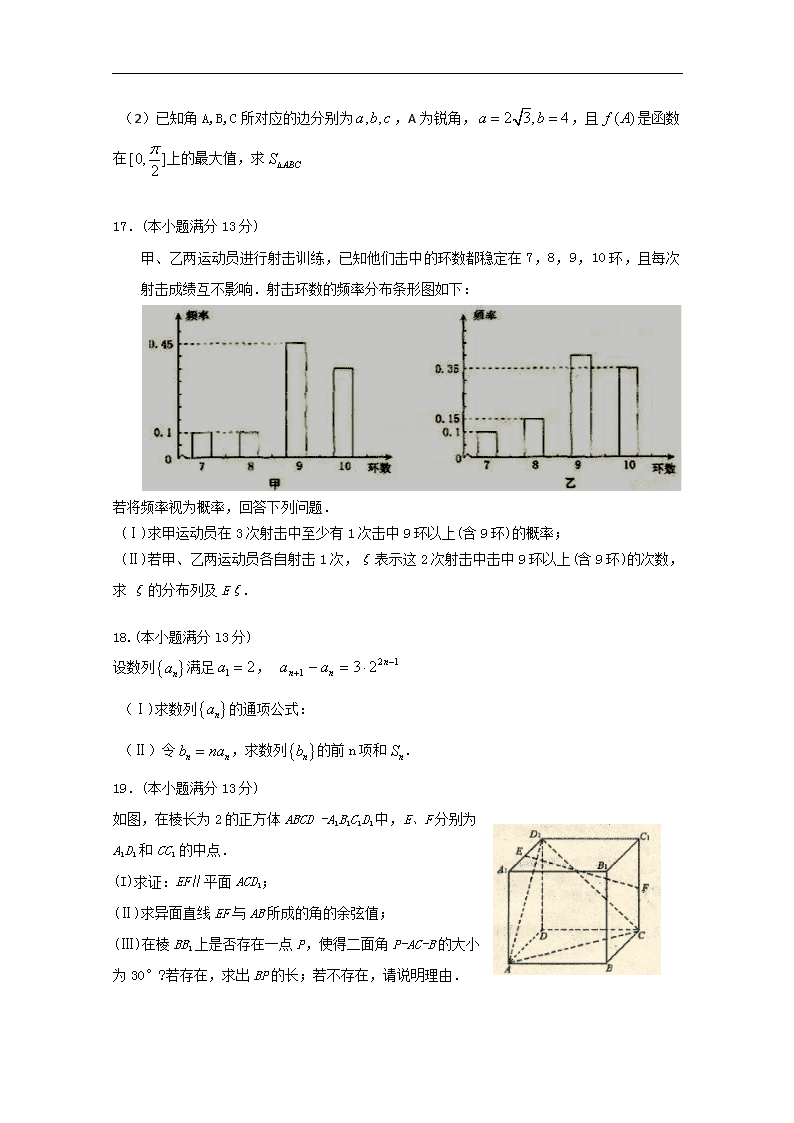解答应写出文字说明、证明过程或演算步骤）.‎ ‎16．（本小题满分13分）‎ 已知向量，函数 ‎（1）求函数的最小正周期T和单调递增区间 ‎（2）已知角A,B,C所对应的边分别为，A为锐角，，且是函数在上的最大值，求 ‎17．(本小题满分13分)‎ 甲、乙两运动员进行射击训练，已知他们击中的环数都稳定在7，8，9，10环，且每次射击成绩互不影响．射击环数的频率分布条形图如下：‎ 若将频率视为概率，回答下列问题．‎ ‎ (Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率；‎ ‎ (Ⅱ)若甲、乙两运动员各自射击1次，ξ表示这2次射击中击中9环以上(含9环)的次数，求ξ的分布列及Eξ．‎ ‎18.(本小题满分l3分)‎ 设数列满足， ‎ ‎ （Ⅰ)求数列的通项公式： ‎ ‎ （Ⅱ）令，求数列的前n项和.‎ ‎19．(本小题满分13分)‎ 如图，在棱长为2的正方体ABCD -A1B1C1D1中，E、F分别为A1D1和CC1 的中点．‎ ‎(I)求证：EF∥平面ACD1；‎ ‎(Ⅱ)求异面直线EF与AB所成的角的余弦值；‎ ‎(Ⅲ)在棱BB1上是否存在一点P，使得二面角P-AC-B的大小为30°?若存在，求出BP的长；若不存在，请说明理由．‎ ‎20．(本小题满分14分)‎ ‎ 已知函数 ‎（I）当时，求函数的图像在处的切线方程；‎ ‎（II）判断函数的单调性；‎ ‎（III）求证：‎ ‎21．本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题记分．‎ ‎（1）(本小题满分7分)选修4－2：矩阵与变换 已知矩阵，，矩阵对应的变换把曲线变为曲线C，求Ｃ的方程．‎ ‎（2）(本小题满分7分)选修4－4：坐标系与参数方程 已知曲线C的极坐标方程是．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线的参数方程是 (t为参数)‎ ‎①. 把直线与曲线C的方程化为普通方程 ‎②.求直线与曲线C相交所成弦的弦长．‎ ‎（3)（本小题满分7分）选修4一5：不等式选讲 ‎①.设函数f(x)＝｜x＋1｜－｜x－4｜，解不等式f（x）＜2；‎ ‎②.已知，且，求的最小值．‎ ‎．2014—2015学年漳州八校高三第一次联考理科数学答题卷 ‎（考试时间：120分钟 总分：150分）‎ 题号 一 二 ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ 总分 得分 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 一、 选择题（每小题5分，共50分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 二、填空题（每小题4分，共20分）‎ ‎11、 ； 12、 ；‎ ‎13、 ； 14、 。‎ ‎15、 ；‎ 三解答题：（本题共6个小题，共80分。解答应写出必要的文字说明、证明过程或演算步骤）‎ ‎16．(本小题满分13分)‎ ‎17．(本小题满分13分)‎ ‎18．(本小题满分13分)‎ ‎20．(本小题满分14分)‎ ‎19．(本小题满分13分)‎ ‎21．(本小题满分14分)‎ ‎2014—2015学年漳州八校高三第一次联考理科数学答案 一、选择题：(每小题5分，满分50分)．‎ ‎1．D． 2．C． 3．D． 4． B． 5．D．6．B． 7．C． 8．A． 9．B． 10．D．‎ 二、填空题：(每小题4分，满分20分)．‎ ‎11．－． 12．-20． 13．1． 14．．①②③ 15．‎ 三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．‎ ‎16. (本小题满分13分)‎ ‎ (1)‎ ‎…………………………4分 令得 所以单调递增区间是…………………………………………7分 ‎(2)解: ‎ 因为，则当时，有最大值为3‎ 由余弦定理知，解得c=2………………………………………11分 则 …………………………………………………………13分 ‎17. (本小题满分13分)‎ ‎ (Ⅰ)甲运动员击中10环的概率是：1一0.1—0.1—0.45=0.35. ‎ 设事件A表示“甲运动员射击一次，恰好命中9环以上(含9环，下同)”，‎ 则P(A)=0.35+0.45=0.8. ‎ 事件“甲运动员在3次射击中，至少1次击中9环以上”包含三种情况：‎ 恰有1次击中9环以上，概率为p1=C·0.81·(1-0.8)2=0.096； ‎ 恰有2次击中9环以上，概率为p2=C·0.82·(1-0.8)1=0.384； ‎ 恰有3次击中9环以上，概率为p3=C·0.83·(1-0.8)0=0.512． ‎ 因为上述三个事件互斥，所以甲运动员射击3次，至少1次击中9环以上的概率 p= p1+ p2+ p3=0.992．…………………………………………………………………………5分 ‎(Ⅱ)记“乙运动员射击1次，击中9环以上”为事件B，‎ 则P(B)=1—0.1—0.15=0.75． ‎ ‎ 因为表示2次射击击中9环以上的次数，所以的可能取值是0，1，2. ‎ ‎ 因为P(=2)=0.8·0.75=0.6；‎ P(=1)=0.8·(1-0.75)+(1-0.8)·0.75=0.35；‎ ‎ P(=0)=(1-0.8)·(1-0.75)=0.05．……………………………………………………… 10分 ‎ 所以的分布列是 ξ ‎0‎ ‎1‎ ‎2‎ P ‎0.05‎ ‎0.35‎ ‎0.6‎ ‎ 所以Eξ=0×0.05+1×0.35+2×0.6=1.55．………………………………………13分 ‎18(本小题满分13分)‎ 解：（Ⅰ）由已知，当n≥1时，‎ ‎。…………………………………………………………………………………4分 而 ‎ 所以数列{}的通项公式为。……………………………………………6分 ‎（Ⅱ）由知 ‎ ①‎ 从而 ②‎ ‎①-②得 ‎ 。‎ 即 ………………………………………………………………13分 ‎19. (本小题满分13分)‎ 解：如图分别以DA、DC、DD1所在的直线为x 轴、y轴、z轴建立空间直角坐标系D-xyz，‎ 由已知得D(0，0，0)、A(2，0，0)、B(2，2，0)、C(0，2，0)、B1(2，2，2)、D1(0，0，2)、E(1，0，2 )、F(0，2，1)．‎ ‎(Ⅰ)取AD1中点G，则G（1，0，1），=（1，-2，1），又=（-1，2，-1），由=，‎ ‎∴与共线．从而ＥＦ∥ＣＧ，∵CG平面ACD1，EF平面ACD1，∴EF∥平面ACD1. ………………………………………………………………4分 ‎(Ⅱ) ∵=(0,2，0)，‎ cos<,>=，‎ ‎∴异面直线EF与AB所成角的余弦值为.…………………………………………………8分 ‎(Ⅲ)假设满足条件的点P存在，可设点P(2，2，t)(0=30°或<，>=150°，‎ ‎∴|cos<，>|=，‎ 即，解得 ‎∵，∴在棱BB1上存在一点P，当BP的长为时，‎ 二面角P-AC-B的大小为30°. ………………………………………………………………13分 ‎20. (本小题满分14分)‎ 解：（I）当时，，‎ ‎(0)=3,所求得切线的斜率为3.‎ 又切点为。‎ 故所求的切线方程为。…………………………………………………………………4分 ‎（II）‎ ①当时，‎ ②当时，由得；‎ 由得。‎ 综上，当，函数在上单调递增；‎ 当时，函数在上单调递减，在上单调递增。…8分 ‎（III）证法一：由（II）可知，当时，‎ 在上单调递增。‎ 当时，，即。‎ 令则 另一方面，即，.‎ ‎………………………………………………………………14分 证法二：构造函数 当时，，‎ 函数在上单调递增。‎ 函数，即。‎ ‎，，即，‎ 令，则有。‎ ‎21．(本题满分14分)‎ ‎（1）（本小题满分7分）‎ 解：，设是所求曲线C上的任意一点，它是曲线上点在矩阵变换下的对应点，则有，即所以又点在曲线上，故，从而，所求曲线C的方程为．……………………………………………………………………7分 ‎（2）（本小题满分7分）‎ 解：①.曲线C的极坐标方程化为直角坐标方程为，即. ‎ 直线的参数方程化为普通方程为.………………………………4分 ‎②.曲线C的圆心（2，0）到直线的距离为，‎ 所以直线与曲线C相交所成的弦的弦长为．………………………………7分 ‎（3）（本小题满分7分）‎ ‎①∵f(x)＝|x＋1|－|x－4|＝ ‎∴由f(x)＜2得x＜.……………………………………………………………………………4分 ‎②.解：注意到，且为定值，‎ 利用柯西不等式得到，‎ 从而，当且仅当时取“＝”号，‎ 所以的最小值为3．………………………………………………………………7分