【新教材】2020-2021学年高中人教A版数学必修第二册课件：8-6-2　直线与平面垂直 44页

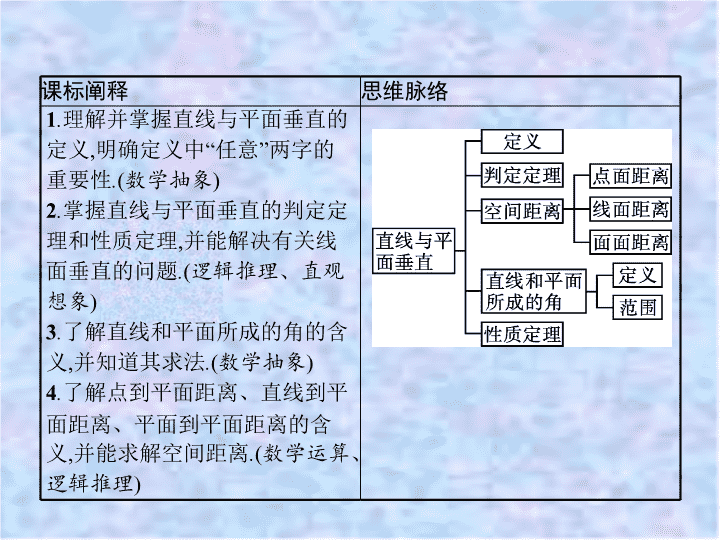
8 . 6 . 2 　 直线与平面垂直 课标阐释 思维脉络 1 . 理解并掌握直线与平面垂直的定义 , 明确定义中 “ 任意 ” 两字的重要性 . ( 数学抽象 ) 2 . 掌握直线与平面垂直的判定定理和性质定理 , 并能解决有关线面垂直的问题 . ( 逻辑推理、直观想象 ) 3 . 了解直线和平面所成的角的含义 , 并知道其求法 . ( 数学抽象 ) 4 . 了解点到平面距离、直线到平面距离、平面到平面距离的 含 义 , 并能求解空间距离 . ( 数学运算、逻辑推理 ) 激趣诱思 知识点拨 唐代诗人王维在他的诗《使至塞上》中写下千古绝句 :“ 大漠孤烟直 , 长河落日圆 . ” 前一句大漠孤烟直中的意境是 : 荒凉的大漠中 , 一缕青烟从烽火台上冲天而起 , 给荒凉的大漠带来了一丝活力 . 从数学的角度看这一景象 , 它充分体现了空间中直线与平面垂直的问题 . 激趣诱思 知识点拨 知识点一、直线与平面垂直的 定义 定义 一般地 , 如果直线 l 与平面 α 内的 任意一条 直线都垂直 , 我们就说直线 l 与平面 α 互相垂直 记法 l ⊥ α 有关 概念 直线 l 叫做平面 α 的 垂线 , 平面 α 叫做直线 l 的 垂面 . 直线与平面垂直时 , 它们唯一的公共点 P 叫做 垂足 图示 画法 画直线与平面垂直时 , 通常把直线画成与表示平面的平行四边形的一边垂直 激趣诱思 知识点拨 名师点析 (1) 定义中的 “ 任意一条 ” 与 “ 任何直线 ”“ 所有直线 ” 意义相同 , 但与 “ 无数条直线 ” 不同 , 即定义是说这条直线和平面内所有直线都垂直 . (2) 直线和平面垂直是直线与平面相交的一种特殊情况 . 激趣诱思 知识点拨 微练习 直线 l 与平面 α 内的无数条直线垂直 , 则 ( 　　 ) A. l 和 α 相互平行 B. l 和 α 相互垂直 C. l 在平面 α 内 D. 不能确定 解析 : 直线 l 和 α 相互平行或直线 l 和 α 相互垂直或直线 l 在平面 α 内都有可能 , 如图所示 . 答案 : D 激趣诱思 知识点拨 知识点二、直线与平面垂直的判定 定理 文字 语言 如果一条直线与一个平面内的两条 相交 直线垂直 , 那么该直线与此平面垂直 图形 语言 符号 语言 l ⊥ a,l ⊥ b,a ⊂ α ,b ⊂ α , a∩b=P ⇒ l ⊥ α 作用 判断直线与平面 垂直 激趣诱思 知识点拨 名师点析 (1)“ 两条相交直线 ” 是关键词语 , 是不可忽视的条件 . (2) 要证一条直线与一个平面垂直 , 只需在平面内找到两条相交的直线都和该直线垂直即可 , 不需要找到所有直线 , 而且这两条相交直线是否和已知直线有公共点是无关紧要的 . (3) 定理体现了相互转化的数学思想 , 即由线线垂直转化为线面垂直 . 激趣诱思 知识点拨 微练习 (1) 若三条直线 OA , OB , OC 两两垂直 , 则直线 OA 垂直于 ( 　　 ) A. 平面 OAB 　　　 B. 平面 OAC C . 平面 OBC D. 平面 ABC 答案 : C (2) 判断下列说法是否正确 , 正确的在后面的括号内画“ √ ” , 错误的画“ ×” . ① 若直线垂直于平面内的两条直线 , 则这条直线与平面垂直 . ( 　　 ) ② 若直线垂直于梯形的两腰所在的直线 , 则这条直线垂直于两底边所在的直线 . ( 　　 ) ③ 若直线垂直于梯形的两底边所在的直线 , 则这条直线垂直于两腰所在的直线 . ( 　　 ) 答案 : ①× 　 ② √ 　 ③ × 激趣诱思 知识点拨 知识点三、直线与平面所成的 角   一条直线 l 与一个平面 α 相交 , 但不与这个平面垂直 , 这条直线叫做这个平面的斜线 , 斜线和平面的交点 A 叫做斜足 . 过斜线上斜足以外的一点 P 向平面 α 引 垂线 PO , 过垂足 O 和斜足 A 的直线 AO 叫做斜线在这个平面上的射影 . 平面的一条斜线和它在平面上的射影所成的角 , 叫做这条直线和这个平面所成的角 . 名师点析 (1) 斜线在平面上的射影是过斜足和垂足的一条直线而不是线段 . (2) 直线与平面所成的角 θ 的取值范围是 0°≤ θ ≤90° . 激趣诱思 知识点拨 微练习 如图 , 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , 直线 AB 1 与平面 ABCD 所成的角等于 　　　　　 ; AB 1 与平面 ADD 1 A 1 所成的角等于 　　　　　 ; AB 1 与平面 DCC 1 D 1 所成的角等于 　　　　　 .  解析 : ∠ B 1 AB 为 AB 1 与平面 ABCD 所成的角 , 即 45°; ∠ B 1 AA 1 为 AB 1 与平面 ADD 1 A 1 所成的角 , 即 45°; AB 1 与平面 DCC 1 D 1 平行 , 即所成的角为 0° . 答案 : 45° 　 45° 　 0° 激趣诱思 知识点拨 知识点四、空间距离 1 . 过一点作 垂直 于已知平面的直线 , 则该点与 垂足 间的线段 , 叫做这个点到该平面的垂线段 , 垂线段的长度 叫做这个点到该平面的距离 . 2 . 一条直线与一个平面 平行 时 , 这条直线上任意一点到这个平面的距离 , 叫做这条直线到这个平面的距离 . 3 . 如果两个平面 平行 , 那么其中一个平面内的任意一点到另一个平面的距离都 相等 , 我们把它叫做这两个平行平面间的距离 . 激趣诱思 知识点拨 微练习 已知在正方体 ABCD-A 1 B 1 C 1 D 1 中 , AB= 2, 则点 C 到平面 BDD 1 B 1 的距离为 ( 　　 ) 解析 : 如图 , 连接 AC , 与 DB 交于点 O , 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , ∵ DB ⊥ AC , BB 1 ⊥ AC , BB 1 ∩ DB=B , ∴ AC ⊥ 平面 BDD 1 B 1 . 答案 : B 激趣诱思 知识点拨 知识点五、直线与平面垂直的性质 定理 文字语言 垂直于同一个平面的两条直线 平行 符号语言 ⇒ a ∥ b 图形语言 作 　 用 证明两条直线 平行 激趣诱思 知识点拨 微思考   在长方体 ABCD-A'B'C'D' 中 , 棱 AA' , BB' 所在直线与平面 ABCD 位置关系如何 ? 这两条直线又有什么样的位置关系 ? 提示 : 棱 AA' , BB' 所在直线都与平面 ABCD 垂直 ; 这两条直线互相平行 . 激趣诱思 知识点拨 微练习 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , 若直线 l ( 与直线 BB 1 不重合 ) ⊥ 平面 A 1 C 1 , 则 ( 　　 ) A. B 1 B ⊥ l B. B 1 B ∥ l C. B 1 B 与 l 异面但不垂直 D. B 1 B 与 l 相交但不垂直 解析 : 因为 B 1 B ⊥ 平面 A 1 C 1 , 又因为 l ⊥ 平面 A 1 C 1 , 所以 l ∥ B 1 B. 答案 : B 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 证明直线与平面垂直 例 1 如图所示 , AB ⊥ BC , △ ABC 所在平面外有一点 S , 且 SA=SB=SC , AC 中点为 D. 求证 : SD ⊥ 平面 ABC. 分析 先由等腰三角形 SAC 及 D 为边 AC 的中点 , 得 SD ⊥ AC. 再由 △ SDA ≌△ SDB , 得 SD ⊥ DB. 证明 : ∵ SA=SC , D 为 AC 中点 , ∴ SD ⊥ AC. 在 Rt △ ABC 中 , AD=DC=BD , 又 SA=SB , ∴△ SDA ≌△ SDB. ∴∠ SDA= ∠ SDB , 即 SD ⊥ DB. 又 AC ∩ BD=D , AC ⊂ 平面 ABC , BD ⊂ 平面 ABC , ∴ SD ⊥ 平面 ABC. 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 反思感悟 直线与平面垂直的判定方法 判定直线与平面垂直 , 可以用定义 , 就是证明这条直线与平面内的任一直线垂直 , 但这种方法一般不用 . 最常用也最好用的是直线与平面垂直的判定定理 , 根据定理 , 只需证明这条直线与平面内的两条相交直线垂直即可 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 延伸探究 在本例条件下 , 若 AB=BC , 求证 : BD ⊥ 平面 SAC. 证明 : ∵ BA=BC , D 为 AC 中点 , ∴ BD ⊥ AC. ∵ SD ⊥ 平面 ABC , BD ⊂ 平面 ABC , ∴ BD ⊥ SD , ∵ AC ⊂ 平面 SAC , SD ⊂ 平面 SAC , AC ∩ SD=D , ∴ BD ⊥ 平面 SAC. 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 证明两直线垂直 例 2 如图 , 已知 PA 垂直于 ☉ O 所在的平面 , AB 是 ☉ O 的直径 , C 是 ☉ O 上任意一点 , 求证 : BC ⊥ PC. 分析 首先利用 PA ⊥ 平面 ABC 得到 PA ⊥ BC , 然后根据圆的性质得到 AC ⊥ BC , 进而利用线面垂直判定定理证得 BC ⊥ 平面 PAC , 从而得到 BC ⊥ PC. 证明 : ∵ PA ⊥ 平面 ABC , BC ⊂ 平面 ABC , ∴ PA ⊥ BC. ∵ AB 是 ☉ O 的直径 , ∴ BC ⊥ AC. 又 PA ∩ AC=A , ∴ BC ⊥ 平面 PAC. ∵ PC ⊂ 平面 PAC , ∴ BC ⊥ PC. 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 反思感悟 1 . 直线和平面垂直的定义具有双重作用 : 判定和性质 . 判定是指 , 如果一条直线和平面内的任意一条直线都垂直 , 那么直线就与平面垂直 ; 性质是指 , 如果一条直线垂直于一个平面 , 那么这条直线就垂直于平面内的任意一条直线 , 即 a ⊥ α , b ⊂ α ⇒ a ⊥ b. 2 . 由直线与平面垂直的定义及判定定理 , 就可以由线线垂直得到线面垂直 , 再由线面垂直得到线线垂直 , 即得到线线垂直与线面垂直的相互转化 . 因此 , 要证明两条直线垂直 ( 无论它们是异面还是共面 ), 通常是证明其中的一条直线垂直于另一条直线所在的一个平面 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 延伸探究 若本例中其他条件不变 , 作 AE ⊥ PC 交 PC 于点 E , 求证 : AE ⊥ PB. 证明 : 由【例 2 】知 BC ⊥ 平面 PAC , ∵ AE ⊂ 平面 PAC , ∴ BC ⊥ AE. ∵ PC ⊥ AE , 且 PC ∩ BC=C , PC ⊂ 平面 PBC , BC ⊂ 平面 PBC , ∴ AE ⊥ 平面 PBC. ∵ PB ⊂ 平面 PBC , ∴ AE ⊥ PB. 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 求直线与平面所成的角 例 3 已知四面体 ABCD 的棱长都相等 , Q 是 AD 的中点 , 则 CQ 与平面 BCD 所成的角的正弦值为 　　　　　 .  分析 作 AO ⊥ 平面 BCD , 垂足 为 O , 连接 OD → 取 OD 中点 P , 连接 QP , CP → ∠ QCP 就是斜线 CQ 与 平面 BCD 所成的角 → 求出 sin ∠ QCP 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 解析 : 过点 A 作 AO ⊥ 平面 BCD , 垂足为 O , 连接 OB , OC , OD. 取 OD 中点 P , 连接 QP , CP. 由 AO ⊥ 平面 BCD , 四面体的棱长都相等知点 O 是三角形三边垂直平分线的交点 , 也是三角形角平分线的交点 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 反思感悟 1 . 求斜线与平面所成的角的步骤 : (1) 作角 . 作 ( 或找 ) 出斜线在平面上的射影 , 将空间角 ( 斜线与平面所成的角 ) 转化为平面角 ( 两条相交直线所成的锐角 ) . (2) 证明 . 证明找出的平面角是斜线与平面所成的角 . (3) 计算 . 通常在垂线段、斜线和射影所组成的直角三角形中计算 . 2 . 在上述步骤中 , 作角是关键 , 而确定斜线在平面内的射影是作角的关键 , 几何图形的特征是找射影的依据 , 图形中的特殊点是突破口 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 变式训练 1 如图 , 在 Rt △ BMC 中 , 斜边 BM= 5, 它在平面 ABC 上的射影为直线 AB , 垂足为 A , 线段 AB 的长为 4, ∠ MBC= 60°, 则 MC 与平面 CAB 所成角的正弦值为 　　　　　 .  探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 解析 : 由题意知 , MA ⊥ 平面 ABC , ∴ MC 在平面 CAB 内的射影为 AC. ∴∠ MCA 即为直线 MC 与平面 CAB 所成的角 . ∵ 在 Rt △ MBC 中 , BM= 5, ∠ MBC= 60°, 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 空间距离的求法 例 4 如图 , 已知正方形 ABCD 的边长为 4, CG ⊥ 平面 ABCD , CG= 2, E , F 分别是 AB , AD 的中点 , 求点 B 到平面 GEF 的距离 . 分析 因为与平面平行的直线上所有点到平面的距离相等 , 可用转移法将该点到平面的距离转化为求另一点到该平面的距离 , 为此要寻找过点 B 与平面 GEF 平行的直线 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 解 : 连接 BD , AC , EF 和 BD 分别交 AC 于 H , O , 连接 GH , 作 OK ⊥ GH 于点 K. ∵ 四边形 ABCD 为正方形 , E , F 分别为 AB , AD 的中点 , ∴ EF ∥ BD , H 为 AO 的中点 . ∵ BD ∥ EF , BD ⊄ 平面 GFE , ∴ BD ∥ 平面 GFE. ∴ 点 B 与平面 GEF 的距离就是点 O 到平面 GEF 的距离 . ∵ BD ⊥ AC , ∴ EF ⊥ AC. ∵ GC ⊥ 平面 ABCD , ∴ GC ⊥ EF. ∵ GC ∩ AC=C , ∴ EF ⊥ 平面 GCH. ∵ OK ⊂ 平面 GCH , ∴ EF ⊥ OK. 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 ∵ OK ⊥ GH , GH ∩ EF=H , ∴ OK ⊥ 平面 GEF , 即 OK 的长就是点 B 到平面 GEF 的距离 . ∵ 正方形 ABCD 的边长为 4, CG= 2 , 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 反思感悟 求点到平面的距离一般有两种方法 (1) 构造法 : 根据定义构造垂直于面的直线 , 确定垂足位置 , 将所求线段化归到三角形中求解 . (2) 等积变换法 : 将所求距离看作某个几何体 ( 多为棱锥 ) 的高 , 利用体积相等建立方程求解 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 延伸探究 本题条件不变 , 如果求直线 BD 到平面 GEF 的距离呢 ? 提示 : 先证明 BD ∥ 平面 GEF , 将直线到平面的距离转化为求点 O 到平面的距离 , 过程和答案与例题一致 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 变式训练 2 已知正方体 ABCD-A 1 B 1 C 1 D 1 的棱长 为 , 平面 AB 1 D 1 到平面 BC 1 D 的距离为 ( 　　 ) 答案 : C 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 直线与平面垂直的性质的应用 例 5 如图 , 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , EF 与异面直线 AC , A 1 D 都垂直相交 . 求证 : EF ∥ BD 1 . 分析 连接 AB 1 , B 1 C , BD , B 1 D 1 , 证明 EF 与 BD 1 都与平面 AB 1 C 垂直 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 证明 : 连接 AB 1 , B 1 C , BD , B 1 D 1 , 如图 . ∵ DD 1 ⊥ 平面 ABCD , AC ⊂ 平面 ABCD , ∴ DD 1 ⊥ AC. 又 AC ⊥ BD , BD ∩ DD 1 =D , BD ⊂ 平面 BDD 1 B 1 , DD 1 ⊂ 平面 BDD 1 B 1 , ∴ AC ⊥ 平面 BDD 1 B 1 . 又 BD 1 ⊂ 平面 BDD 1 B 1 , ∴ AC ⊥ BD 1 . 同理 BD 1 ⊥ B 1 C , ∵ AC ∩ B 1 C=C , ∴ BD 1 ⊥ 平面 AB 1 C. ∵ EF ⊥ A 1 D , 且 A 1 D ∥ B 1 C , ∴ EF ⊥ B 1 C. 又 EF ⊥ AC , AC ∩ B 1 C=C , AC ⊂ 平面 AB 1 C , B 1 C ⊂ 平面 AB 1 C , ∴ EF ⊥ 平面 AB 1 C. ∴ EF ∥ BD 1 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 反思感悟 直线与平面垂直的其他性质 (1) 若一条直线垂直于一个平面 , 则它就垂直于这个平面内的任意一条直线 ; (2) 若两条平行线中的一条垂直于一个平面 , 则另一条也垂直于这个平面 ; (3) 若一条直线垂直于两个平行平面中的一个 , 则它必垂直于另一个平面 ; (4) 垂直于同一条直线的两个平面平行 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 变式训练 3 在四棱锥 P-ABCD 中 , PA ⊥ 平面 ABCD , 且四边形 ABCD 是矩形 , AE ⊥ PD 于点 E , l ⊥ 平面 PCD , 求证 : l ∥ AE. 证明 : ∵ PA ⊥ 平面 ABCD , CD ⊂ 平面 ABCD , ∴ PA ⊥ CD. 又 CD ⊥ AD , PA ∩ AD=A , ∴ CD ⊥ 平面 PAD. ∵ AE ⊂ 平面 PAD , ∴ AE ⊥ DC. 又 AE ⊥ PD , PD ∩ CD=D , ∴ AE ⊥ 平面 PCD. ∵ l ⊥ 平面 PCD , ∴ l ∥ AE. 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 转化与化归思想的应用 典例 设四边形 ABCD 是空间四边形 , AB=AD , CB=CD , 求证 : AC ⊥ BD. 分析 要证空间直线 AC ⊥ BD , 从题目条件上看似无从入手 , 可将空间问题转化为平面问题考虑 , 若取 BD 的中点 E , 则证 BD ⊥ AC 转化为证 BD ⊥ EC , BD ⊥ EA. 证明 : 取 BD 的中点 E , 连接 AE , CE. 由已知 , 在等腰三角形 ABD 和等腰三角形 CBD 中 , 有 AE ⊥ BD , CE ⊥ BD. ∵ AE ∩ CE=E , ∴ BD ⊥ 平面 AEC. ∴ BD ⊥ AC. 方法点睛 要证明直线与直线垂直 , 往往转化为证明线面垂直 , 再利用线面垂直的重要性质得出线线垂直 . 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 1 . 如果一条直线垂直于一个平面内的 : ① 三角形的两边 ; ② 梯形的两边 ; ③ 圆的两条直径 ; ④ 正六边形的两条边 . 则能保证该直线与平面垂直的是 ( 　　 ) A. ①③ B. ①② C. ②④ D. ①④ 解析 : 三角形的两边、圆的两条直径一定是相交直线 , 而梯形的两边、正六边形的两条边不一定相交 , 所以保证直线与平面垂直的是 ①③ . 答案 : A 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 2 . 已知直线 a ⊥ 平面 α , 直线 b ∥ 平面 α , 则 a 与 b 的关系为 ( 　　 ) A. a ∥ b B. a ⊥ b C. a , b 相交不垂直 D. a , b 异面不垂直 解析 : 由 b ∥ α , 过 b 作平面 β , 使 α ∩ β =c , 则 b ∥ c , 且 c ⊂ α . ∵ a ⊥ α , ∴ a ⊥ c. ∴ a ⊥ b. 答案 : B 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 3 . 点 A , B 到平面 α 的距离分别为 4 cm 和 6 cm, 则线段 AB 的中点 M 到平面 α 的距离为 　　　　　 .  解析 : 当 A , B 在平面 α 同侧时 , 由梯形中位线定理可得点 M 到平面 α 的距离为 5 cm; 当 A , B 在平面 α 异侧时 , 由相似三角形列比例式可得距离为 1 cm . 答案 : 1 cm 或 5 cm 4 . 已知 m , n , l 是直线 , α , β 是平面 , α ⊥ β , α ∩ β =l , n ⊂ β , n ⊥ l , m ⊥ α , 则直线 m 与 n 的位置关系是 　　　　　 .  解析 : ∵ α ⊥ β , α ∩ β =l , n ⊂ β , n ⊥ l , ∴ n ⊥ α . 又 m ⊥ α , ∴ m ∥ n. 答案 : 平行 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 5 . 在长方体 ABCD-A 1 B 1 C 1 D 1 中 , AB = , BC=AA 1 = 1, 则 BD 1 与平面 A 1 B 1 C 1 D 1 所成的角的大小为 　　　　　 .  解析 : 如图所示 , 连接 B 1 D 1 , 则 B 1 D 1 是 BD 1 在平面 A 1 B 1 C 1 D 1 上的射影 , 则 ∠ BD 1 B 1 是 BD 1 与平面 A 1 B 1 C 1 D 1 所成的角 . 则 ∠ BD 1 B 1 = 30° . 答案 : 30° 探究一 探究二 探究三 探究四 探究五 素养形成 当堂检测 6 . 如图 , 四边形 ABCD 为矩形 , AD ⊥ 平面 ABE , F 为 CE 上的点 , 且 BF ⊥ 平面 ACE. 求证 : AE ⊥ BE. 证明 : ∵ AD ⊥ 平面 ABE , AD ∥ BC , ∴ BC ⊥ 平面 ABE. 又 AE ⊂ 平面 ABE , ∴ AE ⊥ BC. ∵ BF ⊥ 平面 ACE , AE ⊂ 平面 ACE , ∴ AE ⊥ BF. ∵ BF ⊂ 平面 BCE , BC ⊂ 平面 BCE , BF ∩ BC=B , ∴ AE ⊥ 平面 BCE. 又 BE ⊂ 平面 BCE , ∴ AE ⊥ BE.