2013年重庆市高考数学试卷（文科） 22页

‎2013年重庆市高考数学试卷（文科）‎ ‎　‎ 一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个备选项中，只有一个选项是符合题目要求的．‎ ‎1．（5分）已知全集U={1，2，3，4}，集合A={1，2}，B={2，3}，则∁U（A∪B）=（　　）‎ A．{1，3，4} B．{3，4} C．{3} D．{4}‎ ‎2．（5分）命题“对任意x∈R，都有x2≥0”的否定为（　　）‎ A．存在x0∈R，使得x02＜0 B．对任意x∈R，使得x2＜0‎ C．存在x0∈R，都有 D．不存在x∈R，使得x2＜0‎ ‎3．（5分）函数y=的定义域为（　　）‎ A．（﹣∞，2） B．（2，+∞） C．（2，3）∪（3，+∞） D．（2，4）∪（4，+∞）‎ ‎4．（5分）设P是圆（x﹣3）2+（y+1）2=4上的动点，Q是直线x=﹣3上的动点，则|PQ|的最小值为（　　）‎ A．6 B．4 C．3 D．2‎ ‎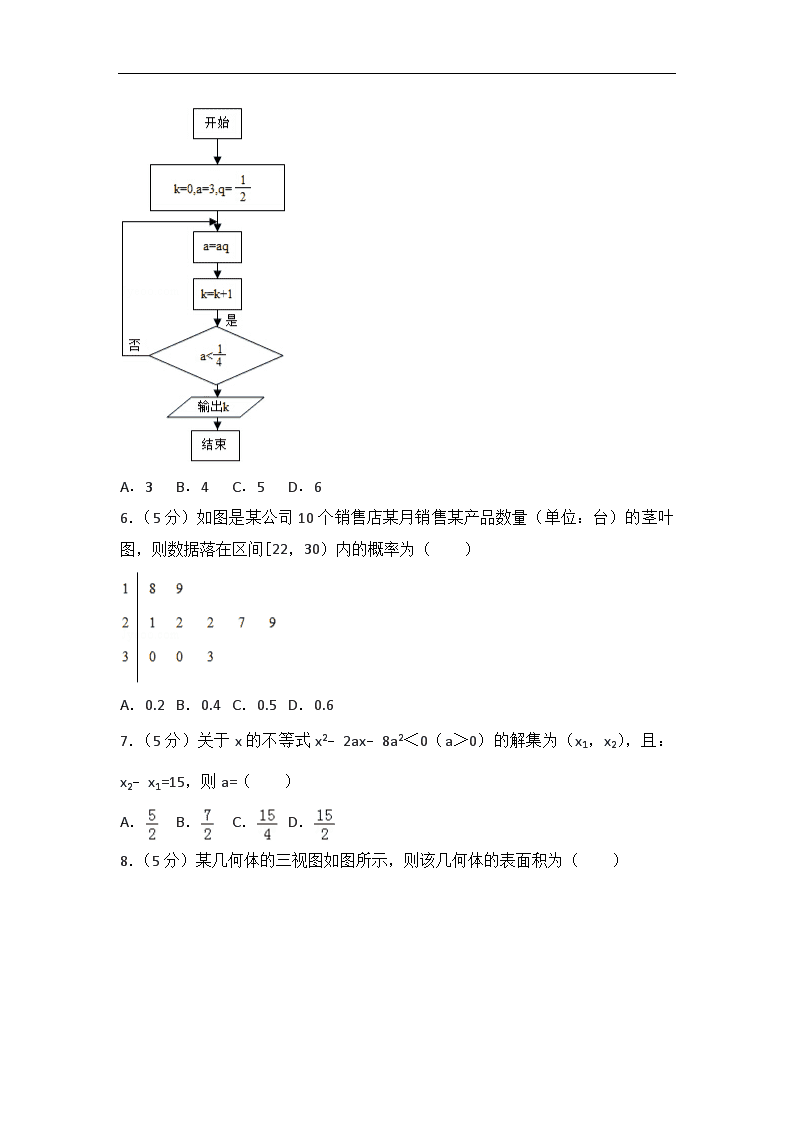5．（5分）执行如图所示的程序框图，输出的k值为（　　）‎ A．3 B．4 C．5 D．6‎ ‎6．（5分）如图是某公司10个销售店某月销售某产品数量（单位：台）的茎叶图，则数据落在区间[22，30）内的概率为（　　）‎ A．0.2 B．0.4 C．0.5 D．0.6‎ ‎7．（5分）关于x的不等式x2﹣2ax﹣8a2＜0（a＞0）的解集为（x1，x2），且：x2﹣x1=15，则a=（　　）‎ A． B． C． D．‎ ‎8．（5分）某几何体的三视图如图所示，则该几何体的表面积为（　　）‎ A．180 B．200 C．220 D．240‎ ‎9．（5分）已知函数f（x）=ax3+bsinx+4（a，b∈R），f（lg（log210））=5，则f（lg（lg2））=（　　）‎ A．﹣5 B．﹣1 C．3 D．4‎ ‎10．（5分）设双曲线C的中心为点O，若有且只有一对相交于点O，所成的角为60°的直线A1B1和A2B2，使|A1B1|=|A2B2|，其中A1、B1和A2、B2分别是这对直线与双曲线C的交点，则该双曲线的离心率的取值范围是（　　）‎ A． B． C． D．‎ ‎　‎ 二．填空题：本大题共5小题，考生作答5小题，每小题5分，共25分．把答案填写在答题卡相应位置上．‎ ‎11．（5分）已知复数z=1+2i（i是虚数单位），则|z|=　　．‎ ‎12．（5分）若2、a、b、c、9成等差数列，则c﹣a=　　．‎ ‎13．（5分）若甲、乙、丙三人随机地站成一排，则甲、乙两人相邻而站的概率为　　．‎ ‎14．（5分）OA为边，OB为对角线的矩形中，，，则实数k=　　．‎ ‎15．（5分）设0≤α≤π，不等式8x2﹣（8sinα）x+cos2α≥0对x∈R恒成立，则α的取值范围为　　．‎ ‎　‎ 三．解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ 如图，椭圆的中心为原点O，长轴在x轴上，离心率，过左焦点F1作x轴的垂线交椭圆于A、A′两点，|AA′|=4．‎ ‎（Ⅰ）求该椭圆的标准方程；‎ ‎（Ⅱ）取平行于y轴的直线与椭圆相交于不同的两点P、P′，过P、P′作圆心为Q的圆，使椭圆上的其余点均在圆Q外．求△PP'Q的面积S的最大值，并写出对应的圆Q的标准方程．‎ ‎16．（13分）设数列{an}满足：a1=1，an+1=3an，n∈N+．‎ ‎（Ⅰ）求{an}的通项公式及前n项和Sn；‎ ‎（Ⅱ）已知{bn}是等差数列，Tn为前n项和，且b1=a2，b3=a1+a2+a3，求T20．‎ ‎17．（13分）从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi（单位：千元）与月储蓄yi（单位：千元）的数据资料，算得，，，．‎ ‎（Ⅰ）求家庭的月储蓄y对月收入x的线性回归方程y=bx+a；‎ ‎（Ⅱ）判断变量x与y之间是正相关还是负相关；‎ ‎（Ⅲ）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．‎ 附：线性回归方程y=bx+a中，，，其中，为样本平均值，线性回归方程也可写为．‎ ‎18．（13分）在△ABC中，内角A、B、C的对边分别是a、b、c，且a2=b2+c2+‎ bc．‎ ‎（Ⅰ）求A；‎ ‎（Ⅱ）设a=，S为△ABC的面积，求S+3cosBcosC的最大值，并指出此时B的最值．‎ ‎19．（12分）如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，PA=2，BC=CD=2，∠ACB=∠ACD=．‎ ‎（Ⅰ）求证：BD⊥平面PAC；‎ ‎（Ⅱ）若侧棱PC上的点F满足PF=7FC，求三棱锥P﹣BDF的体积．‎ ‎20．（12分）某村庄拟修建一个无盖的圆柱形蓄水池（不计厚度）．设该蓄水池的底面半径为r米，高为h米，体积为V立方米．假设建造成本仅与表面积有关，侧面积的建造成本为100元/平方米，底面的建造成本为160元/平方米，该蓄水池的总建造成本为12000π元（π为圆周率）．‎ ‎（Ⅰ）将V表示成r的函数V（r），并求该函数的定义域；‎ ‎（Ⅱ）讨论函数V（r）的单调性，并确定r和h为何值时该蓄水池的体积最大．‎ ‎　‎ ‎2013年重庆市高考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个备选项中，只有一个选项是符合题目要求的．‎ ‎1．（5分）（2013•重庆）已知全集U={1，2，3，4}，集合A={1，2}，B={2，3}，则∁U（A∪B）=（　　）‎ A．{1，3，4} B．{3，4} C．{3} D．{4}‎ ‎【分析】根据A与B求出两集合的并集，由全集U，找出不属于并集的元素，即可求出所求的集合．‎ ‎【解答】解：∵A={1，2}，B={2，3}，‎ ‎∴A∪B={1，2，3}，‎ ‎∵全集U={1，2，3，4}，‎ ‎∴∁U（A∪B）={4}．‎ 故选D ‎　‎ ‎2．（5分）（2013•重庆）命题“对任意x∈R，都有x2≥0”的否定为（　　）‎ A．存在x0∈R，使得x02＜0 B．对任意x∈R，使得x2＜0‎ C．存在x0∈R，都有 D．不存在x∈R，使得x2＜0‎ ‎【分析】根据全称命题“∀x∈M，p（x）”的否定为特称命题：“∃x0∈M，￢p（x）”即可得出．‎ ‎【解答】解：根据全称命题的否定是特称命题可得：‎ 命题“对任意x∈R，都有x2≥0”的否定为“∃x0∈R，使得”．‎ 故选A．‎ ‎　‎ ‎3．（5分）（2013•重庆）函数y=的定义域为（　　）‎ A．（﹣∞，2） B．（2，+∞） C．（2，3）∪（3，+∞） D．（2，4）∪（4，+∞）‎ ‎【分析】根据“让解析式有意义”的原则，对数的真数大于0，分母不等于0，建立不等式，解之即可．‎ ‎【解答】解：要使原函数有意义，则，‎ 解得：2＜x＜3，或x＞3‎ 所以原函数的定义域为（2，3）∪（3，+∞）．‎ 故选C．‎ ‎　‎ ‎4．（5分）（2013•重庆）设P是圆（x﹣3）2+（y+1）2=4上的动点，Q是直线x=﹣3上的动点，则|PQ|的最小值为（　　）‎ A．6 B．4 C．3 D．2‎ ‎【分析】过圆心A作AQ⊥直线x=﹣3，与圆交于点P，此时|PQ|最小，由此能求出|PQ|的最小值．‎ ‎【解答】解：过圆心A作AQ⊥直线x=﹣3，‎ 与圆交于点P，此时|PQ|最小，‎ 由圆的方程得到A（3，﹣1），半径r=2，‎ 则|PQ|=|AQ|﹣r=6﹣2=4．‎ 故选：B．‎ ‎　‎ ‎5．（5分）（2015•北京）执行如图所示的程序框图，输出的k值为（　　）‎ A．3 B．4 C．5 D．6‎ ‎【分析】模拟执行程序框图，依次写出每次循环得到的a，k的值，当a=时满足条件a＜，退出循环，输出k的值为4．‎ ‎【解答】解：模拟执行程序框图，可得 k=0，a=3，q=‎ a=，k=1‎ 不满足条件a＜，a=，k=2‎ 不满足条件a＜，a=，k=3‎ 不满足条件a＜，a=，k=4‎ 满足条件a＜，退出循环，输出k的值为4．‎ 故选：B．‎ ‎　‎ ‎6．（5分）（2013•重庆）如图是某公司10个销售店某月销售某产品数量（单位：台）的茎叶图，则数据落在区间[22，30）内的概率为（　　）‎ A．0.2 B．0.4 C．0.5 D．0.6‎ ‎【分析】由茎叶图10个原始数据数据，数出落在区间[22，30）内的个数，由古典概型的概率公式可得答案．‎ ‎【解答】解：由茎叶图10个原始数据，数据落在区间[22，30）内的共有4个，包括2个22，1个27，1个29，则数据落在区间[22，30）内的概率为=0.4．‎ 故选B．‎ ‎　‎ ‎7．（5分）（2013•重庆）关于x的不等式x2﹣2ax﹣8a2＜0（a＞0）的解集为（x1，x2），且：x2﹣x1=15，则a=（　　）‎ A． B． C． D．‎ ‎【分析】利用不等式的解集以及韦达定理得到两根关系式，然后与已知条件化简求解a的值即可．‎ ‎【解答】解：因为关于x的不等式x2﹣2ax﹣8a2＜0（a＞0）的解集为（x1，x2），‎ 所以x1+x2=2a…①，‎ x1•x2=﹣8a2…②，‎ 又x2﹣x1=15…③，‎ ‎①2﹣4×②可得（x2﹣x1）2=36a2，代入③可得，152=36a2，解得a==，‎ 因为a＞0，所以a=．‎ 故选：A．‎ ‎　‎ ‎8．（5分）（2013•重庆）某几何体的三视图如图所示，则该几何体的表面积为（　　）‎ A．180 B．200 C．220 D．240‎ ‎【分析】由三视图可知：该几何体是一个横放的直四棱柱，高为10；其底面是一个等腰梯形，上下边分别为2，8，高为4；据此可求出该几何体的表面积．‎ ‎【解答】解：由三视图可知：该几何体是一个横放的直四棱柱，高为10；‎ 其底面是一个等腰梯形，上下边分别为2，8，高为4．‎ ‎∴S表面积=2××（2+8）×4+2×5×10+2×10+8×10=240．‎ 故选D．‎ ‎　‎ ‎9．（5分）（2013•重庆）已知函数f（x）=ax3+bsinx+4（a，b∈R），f（lg（log210））=5，则f（lg（lg2））=（　　）‎ A．﹣5 B．﹣1 C．3 D．4‎ ‎【分析】由题设条件可得出lg（log210）与lg（lg2）互为相反数，再引入g（x）=ax3+bsinx，使得f（x）=g（x）+4，利用奇函数的性质即可得到关于f（lg（lg2））的方程，解方程即可得出它的值 ‎【解答】解：∵lg（log210）+lg（lg2）=lg1=0，‎ ‎∴lg（log210）与lg（lg2）互为相反数 则设lg（log210）=m，那么lg（lg2）=﹣m 令f（x）=g（x）+4，即g（x）=ax3+bsinx，此函数是一个奇函数，故g（﹣m）=﹣g（m），‎ ‎∴f（m）=g（m）+4=5，g（m）=1‎ ‎∴f（﹣m）=g（﹣m）+4=﹣g（m）+4=3．‎ 故选C．‎ ‎　‎ ‎10．（5分）（2013•重庆）设双曲线C的中心为点O，若有且只有一对相交于点O，所成的角为60°的直线A1B1和A2B2，使|A1B1|=|A2B2|，其中A1、B1和A2、B2分别是这对直线与双曲线C的交点，则该双曲线的离心率的取值范围是（　　）‎ A． B． C． D．‎ ‎【分析】不妨令双曲线的方程为，由|A1B1|=|A2B2|及双曲线的对称性知A1，A2，B1，B2关于x轴对称，由满足条件的直线只有一对，得，由此能求出双曲线的离心率的范围．‎ ‎【解答】解：不妨令双曲线的方程为，‎ 由|A1B1|=|A2B2|及双曲线的对称性知A1，A2，B1，B2关于x轴对称，如图，‎ 又∵满足条件的直线只有一对，‎ 当直线与x轴夹角为30°时，双曲线的渐近线与x轴夹角大于30°，‎ 双曲线与直线才能有交点A1，A2，B1，B2，‎ 若双曲线的渐近线与x轴夹角等于30°，则无交点，‎ 则不可能存在|A1B1|=|A2B2|，‎ 当直线与x轴夹角为60°时，双曲线渐近线与x轴夹角大于60°，‎ 双曲线与直线有一对交点A1，A2，B1，B2，‎ 若双曲线的渐近线与x轴夹角等于60°，也满足题中有一对直线，‎ 但是如果大于60°，则有两对直线．不符合题意，‎ ‎∴tan30°，即，‎ ‎∴，‎ ‎∵b2=c2﹣a2，∴，∴，‎ ‎∴，‎ ‎∴双曲线的离心率的范围是．‎ 故选：A．‎ ‎　‎ 二．填空题：本大题共5小题，考生作答5小题，每小题5分，共25分．把答案填写在答题卡相应位置上．‎ ‎11．（5分）（2013•重庆）已知复数z=1+2i（i是虚数单位），则|z|=　　．‎ ‎【分析】直接利用复数的模的求法公式，求解即可．‎ ‎【解答】解：复数z=1+2i（i是虚数单位），则|z|==．‎ 故答案为：．‎ ‎　‎ ‎12．（5分）（2013•重庆）若2、a、b、c、9成等差数列，则c﹣a=　　．‎ ‎【分析】由等差数列的性质可得2b=2+9，解之可得b值，再由等差中项可得a，c的值，作差即可得答案．‎ ‎【解答】解：由等差数列的性质可得2b=2+9，解得b=，‎ 又可得2a=2+b=2+=，解之可得a=，‎ 同理可得2c=9+=，解得c=，‎ 故c﹣a=﹣==‎ 故答案为：‎ ‎　‎ ‎13．（5分）（2013•重庆）若甲、乙、丙三人随机地站成一排，则甲、乙两人相邻而站的概率为　　．‎ ‎【分析】甲、乙两人相邻，可以把两个元素看做一个元素同其他元素进行排列，然后代入古典概率的求解公式即可求解 ‎【解答】解：记甲、乙两人相邻而站为事件A 甲、乙、丙三人随机地站成一排的所有排法有=6，‎ 则甲、乙两人相邻而站，把甲和乙当做一个整体，甲和乙的排列有种，然后把甲乙整体和丙进行排列，有种，因此共有=4种站法 ‎∴=‎ 故答案为：‎ ‎　‎ ‎14．（5分）（2013•重庆）OA为边，OB为对角线的矩形中，，，则实数k=　4　．‎ ‎【分析】由题意可得OA⊥AB，故有 =0，即 ==0，解方程求得k的值．‎ ‎【解答】解：由于OA为边，OB为对角线的矩形中，OA⊥AB，∴=0，‎ 即 ==（﹣3，1）•（﹣2，k）﹣10=6+k﹣10=0，‎ 解得k=4，‎ 故答案为 4．‎ ‎　‎ ‎15．（5分）（2013•重庆）设0≤α≤π，不等式8x2﹣（8sinα）x+cos2α≥0对x∈R恒成立，则α的取值范围为　[0，]∪[，π]　．‎ ‎【分析】由题意可得，△=64sin2α﹣32cos2α≤0即2sin2α﹣（1﹣2sin2α）≤0，解不等式结合0≤α≤π可求α的取值范围．‎ ‎【解答】解：由题意可得，△=64sin2α﹣32cos2α≤0，‎ 得2sin2α﹣（1﹣2sin2α）≤0‎ ‎∴sin2α≤，‎ ‎﹣≤sinα≤，‎ ‎∵0≤α≤π ‎∴α∈[0，]∪[，π]．‎ 故答案为：[0，]∪[，π]．‎ ‎　‎ 三．解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎（2013•重庆）如图，椭圆的中心为原点O，长轴在x轴上，离心率，过左焦点F1作x轴的垂线交椭圆于A、A′两点，|AA′|=4．‎ ‎（Ⅰ）求该椭圆的标准方程；‎ ‎（Ⅱ）取平行于y轴的直线与椭圆相交于不同的两点P、P′，过P、P′作圆心为Q的圆，使椭圆上的其余点均在圆Q外．求△PP'Q的面积S的最大值，并写出对应的圆Q的标准方程．‎ ‎【分析】（Ⅰ）设椭圆方程为，将左焦点横坐标代入椭圆方程可得y=，则，又②，a2=b2+c2③，联立①②③可求得a，b；‎ ‎（Ⅱ）设Q（t，0）（t＞0），圆的半径为r，直线PP′方程为：x=m（m＞t），则圆Q的方程为：（x﹣t）2+y2=r2，联立圆与椭圆方程消掉y得x的二次方程，则△=0①，易求P点坐标，代入圆的方程得等式②，由①②消掉r得m=2t，则，变为关于t的函数，利用基本不等式可求其最大值及此时t值，由对称性可得圆心Q在y轴左侧的情况；‎ ‎【解答】解：（Ⅰ）设椭圆方程为，‎ 左焦点F1（﹣c，0），将横坐标﹣c代入椭圆方程，得y=，‎ 所以①，②，a2=b2+c2③，联立①②③解得a=4，，‎ 所以椭圆方程为：；‎ ‎（Ⅱ）设Q（t，0）（t＞0），圆的半径为r，直线PP′方程为：x=m（m＞t），‎ 则圆Q的方程为：（x﹣t）2+y2=r2，‎ 由得x2﹣4tx+2t2+16﹣2r2=0，‎ 由△=0，即16t2﹣4（2t2+16﹣2r2）=0，得t2+r2=8，①‎ 把x=m代入，得，‎ 所以点P坐标为（m，），代入（x﹣t）2+y2=r2，得，②‎ 由①②消掉r2得4t2﹣4mt+m2=0，即m=2t，‎ ‎=×（m﹣t）=×t=≤‎ ‎×=2，‎ 当且仅当4﹣t2=t2即t=时取等号，‎ 此时t+r=+＜4，椭圆上除P、P′外的点在圆Q外，‎ 所以△PP'Q的面积S的最大值为，圆Q的标准方程为：．‎ 当圆心Q、直线PP′在y轴左侧时，由对称性可得圆Q的方程为，△PP'Q的面积S的最大值仍为为．‎ ‎　‎ ‎16．（13分）（2013•重庆）设数列{an}满足：a1=1，an+1=3an，n∈N+．‎ ‎（Ⅰ）求{an}的通项公式及前n项和Sn；‎ ‎（Ⅱ）已知{bn}是等差数列，Tn为前n项和，且b1=a2，b3=a1+a2+a3，求T20．‎ ‎【分析】（Ⅰ）可得数列{an}是首项为1，公比为3的等比数列，代入求和公式和通项公式可得答案；‎ ‎（Ⅱ）可得b1=3，b3=13，进而可得其公差，代入求和公式可得答案．‎ ‎【解答】解：（Ⅰ）由题意可得数列{an}是首项为1，公比为3的等比数列，‎ 故可得an=1×3n﹣1=3n﹣1，‎ 由求和公式可得Sn==；‎ ‎（Ⅱ）由题意可知b1=a2=3，b3=a1+a2+a3=1+3+9=13，‎ 设数列{bn}的公差为d，可得b3﹣b1=10=2d，解得d=5‎ 故T20=20×3+=1010‎ ‎　‎ ‎17．（13分）（2013•重庆）从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi（单位：千元）与月储蓄yi（单位：千元）的数据资料，算得，，，．‎ ‎（Ⅰ）求家庭的月储蓄y对月收入x的线性回归方程y=bx+a；‎ ‎（Ⅱ）判断变量x与y之间是正相关还是负相关；‎ ‎（Ⅲ）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．‎ 附：线性回归方程y=bx+a中，，，其中，为样本平均值，线性回归方程也可写为．‎ ‎【分析】（Ⅰ）由题意可知n，，，进而可得，，代入可得b值，进而可得a值，可得方程；‎ ‎（Ⅱ）由回归方程x的系数b的正负可判；‎ ‎（Ⅲ）把x=7代入回归方程求其函数值即可．‎ ‎【解答】解：（Ⅰ）由题意可知n=10，===8，===2，‎ 故lxx==720﹣10×82=80，lxy==184﹣10×8×2=24，‎ 故可得b=═=0.3，a==2﹣0.3×8=﹣0.4，‎ 故所求的回归方程为：y=0.3x﹣0.4；‎ ‎（Ⅱ）由（Ⅰ）可知b=0.3＞0，即变量y随x的增加而增加，故x与y之间是正相关；‎ ‎（Ⅲ）把x=7代入回归方程可预测该家庭的月储蓄为y=0.3×7﹣0.4=1.7（千元）．‎ ‎　‎ ‎18．（13分）（2013•重庆）在△ABC中，内角A、B、C的对边分别是a、b、c，且a2=b2+c2+bc．‎ ‎（Ⅰ）求A；‎ ‎（Ⅱ）设a=，S为△ABC的面积，求S+3cosBcosC的最大值，并指出此时B的最值．‎ ‎【分析】（Ⅰ）由余弦定理表示出cosA，将依照等式变形后代入求出cosA的值，由A为三角形的内角，利用特殊角的三角函数值即可求出A的度数；‎ ‎（Ⅱ）由（Ⅰ）求出sinA的值，由三角形的面积公式及正弦定理列出关系式，表示出S，代入已知等式中提取3变形后，利用两角和与差的余弦函数公式化为一个角的余弦函数，由余弦函数的图象与性质即可求出S+3cosBcosC的最大值，以及此时B的值．‎ ‎【解答】解：（Ⅰ）由余弦定理得：cosA===﹣，‎ ‎∵A为三角形的内角，∴A=；‎ ‎（Ⅱ）由（Ⅰ）得sinA=，由正弦定理得：b=，csinA=asinC及a=得：‎ S=bcsinA=••asinC=3sinBsinC，‎ 则S+3cosBcosC=3（sinBsinC+cosBcosC）=3cos（B﹣C），‎ 则当B﹣C=0，即B=C==时，S+3cosBcosC取最大值3．‎ ‎　‎ ‎19．（12分）（2013•重庆）如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，PA=2，BC=CD=2，∠ACB=∠ACD=．‎ ‎（Ⅰ）求证：BD⊥平面PAC；‎ ‎（Ⅱ）若侧棱PC上的点F满足PF=7FC，求三棱锥P﹣BDF的体积．‎ ‎【分析】（Ⅰ）由等腰三角形的性质可得BD⊥AC，再由PA⊥底面ABCD，可得PA⊥BD．再利用直线和平面垂直的判定定理证明BD⊥平面PAC．‎ ‎（Ⅱ）由侧棱PC上的点F满足PF=7FC，可得三棱锥F﹣BCD的高是三棱锥P﹣BCD的高的．求出△BCD的面积S△BCD，再根据三棱锥P﹣BDF的体积 V=VP﹣BCD﹣VF﹣BCD=﹣，运算求得结果．‎ ‎【解答】解：（Ⅰ）∵BC=CD=2，∴△BCD为等腰三角形，再由 ，∴BD⊥AC．‎ 再由PA⊥底面ABCD，可得PA⊥BD．‎ 而PA∩AC=A，故BD⊥平面PAC．‎ ‎（Ⅱ）∵侧棱PC上的点F满足PF=7FC，‎ ‎∴三棱锥F﹣BCD的高是三棱锥P﹣BCD的高的．‎ ‎△BCD的面积S△BCD=BC•CD•sin∠BCD==．‎ ‎∴三棱锥P﹣BDF的体积 V=VP﹣BCD﹣VF﹣BCD=﹣=×‎ ‎==．‎ ‎　‎ ‎20．（12分）（2013•重庆）某村庄拟修建一个无盖的圆柱形蓄水池（不计厚度）．设该蓄水池的底面半径为r米，高为h米，体积为V立方米．假设建造成本仅与表面积有关，侧面积的建造成本为100元/平方米，底面的建造成本为160元/平方米，该蓄水池的总建造成本为12000π元（π为圆周率）．‎ ‎（Ⅰ）将V表示成r的函数V（r），并求该函数的定义域；‎ ‎（Ⅱ）讨论函数V（r）的单调性，并确定r和h为何值时该蓄水池的体积最大．‎ ‎【分析】（I）由已知中侧面积和底面积的单位建造成本，结合圆柱体的侧面积及底面积公式，根据该蓄水池的总建造成本为12000π元，构造方程整理后，可将V表示成r的函数，进而根据实际中半径与高为正数，得到函数的定义域；‎ ‎（Ⅱ）根据（I）中函数的定义值及解析式，利用导数法，可确定函数的单调性，根据单调性，可得函数的最大值点．‎ ‎【解答】解：（Ⅰ）∵蓄水池的侧面积的建造成本为200•πrh元，‎ 底面积成本为160πr2元，‎ ‎∴蓄水池的总建造成本为200•πrh+160πr2元 即200•πrh+160πr2=12000π ‎∴h=（300﹣4r2）‎ ‎∴V（r）=πr2h=πr2•（300﹣4r2）=（300r﹣4r3）‎ 又由r＞0，h＞0可得0＜r＜5‎ 故函数V（r）的定义域为（0，5）‎ ‎（Ⅱ）由（Ⅰ）中V（r）=（300r﹣4r3），（0＜r＜5）‎ 可得V′（r）=（300﹣12r2），（0＜r＜5）‎ ‎∵令V′（r）=（300﹣12r2）=0，则r=5‎ ‎∴当r∈（0，5）时，V′（r）＞0，函数V（r）为增函数 当r∈（5，5）时，V′（r）＜0，函数V（r）为减函数 且当r=5，h=8时该蓄水池的体积最大 ‎　‎ 参与本试卷答题和审题的老师有：sllwyn；沂蒙松；minqi5；zlzhan；w3239003；qiss；xintrl；lincy；吕静；caoqz；wyz123；豫汝王世崇（排名不分先后）‎ ‎2017年2月3日