高考数学专题复习教案： 对数与对数函数 2页

对数与对数函数 主标题：对数与对数函数 副标题：为学生详细的分析对数与对数函数的高考考点、命题方向以及规律总结。‎ 关键词：对数，对数函数 难度：3‎ 重要程度：5‎ 考点剖析：‎ ‎1．理解对数的概念及其运算性质，知道用换底公式将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用；‎ ‎2．理解对数函数的概念及其单调性，掌握对数函数的图象通过的特殊点，会画底数为2,10，的对数函数的图象；‎ ‎3．体会对数函数是一类重要的函数模型；‎ ‎4．了解指数函数y＝ax(a＞0，且a≠1)与对数函数y＝logax(a＞0，且a≠1)互为反函数.‎ 命题方向：高考对该部分的考查多与函数的基本性质相结合综合命题，涉及函数的奇偶性、单调性、零点问题，函数值的求解，函数图象的识别等问题，考查学生分析、解决问题的能力．‎ 规律总结：(1)研究对数型函数的图象时，一般从最基本的对数函数的图象入手，通过平移、伸缩、对称变换得到．特别地，要注意底数a＞1和0＜a＜1的两种不同情况．有些复杂的问题，借助于函数图象来解决，就变得简单了，这是数形结合思想的重要体现．‎ ‎(2)利用单调性可解决比较大小、解不等式、求最值等问题，其基本方法是“同底法”，即把不同底的对数式化为同底的对数式，然后根据单调性来解决．　　　‎ 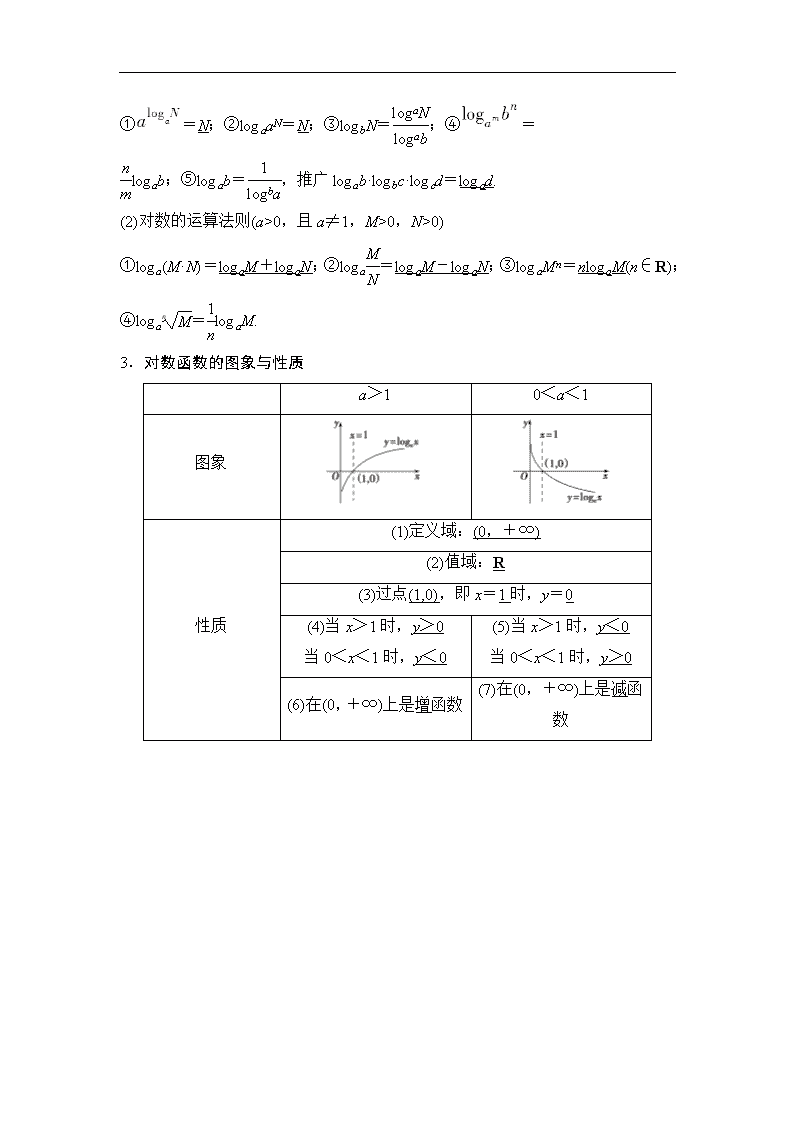知 识 梳 理 ‎1．对数的概念 如果ax＝N(a>0，且a≠1)，那么数x叫做以a为底N的对数，记作x＝logaN，其中a叫做对数的底数，N叫做真数．‎ ‎2．对数的性质与运算法则 ‎(1)对数的性质 几个恒等式(M，N，a，b都是正数，且a，b≠1)‎ ‎①＝N；②logaaN＝N；③logbN＝；④＝‎ logab；⑤logab＝，推广logab·logbc·logcd＝logad.‎ ‎(2)对数的运算法则(a>0，且a≠1，M>0，N>0)‎ ‎①loga(M·N)＝logaM＋logaN；②loga＝logaM－logaN；③logaMn＝nlogaM(n∈R)；④loga＝logaM.‎ ‎3．对数函数的图象与性质 a＞1‎ ‎0＜a＜1‎ 图象 性质 ‎(1)定义域：(0，＋∞)‎ ‎(2)值域：R　　　　‎ ‎(3)过点(1,0)，即x＝1时，y＝0‎ ‎(4)当x＞1时，y＞0‎ 当0＜x＜1时，y＜0‎ ‎(5)当x＞1时，y＜0‎ 当0＜x＜1时，y＞0‎ ‎(6)在(0，＋∞)上是增函数 ‎(7)在(0，＋∞)上是减函数