安徽省蚌埠市怀远县2013届高三联考数学（理）试题 9页

数学试卷(理科)‎ ‎(总分：150分，时间：120分钟)‎ 本试卷分第Ⅰ卷 （选择题）和第Ⅱ卷 (非选择题)两部分 一、选择题。(本题共10小题，每小题5分，共计50分)‎ ‎1．已知复数的虚部是( )‎ ‎ A． B． C． D．‎ ‎2．已知全集,集合，集合，则 ‎ A． B． C． D．‎ ‎3．已知,则 ‎ A．2 B． C．－2 D．－‎ ‎4．设向量满足： ‎ A． B．‎1 ‎ C． D．2‎ ‎5．已知为第二象限角，‎ ‎ A． B． C． D．‎ ‎6．下列命题中错误的是( )‎ ‎ A．命题：“若”‎ B．已知命题P和q，若PVq为假命题，则命题P与q中必一真一假。‎ C．对于命题P:，使得。‎ D．“”是“”的充分不必要条件。‎ ‎7．设奇函数上为单调递减，且则不等式的解集为（ ）‎ A．（－］(0,2］ B．(－2，0］［2，＋］‎ C．(－］［2，＋） D．［－2，0)(0，2］‎ ‎8.下列函数图象是一个函数与其导函数在同一个坐标系中的图象，其中一定错误的是( )‎ ‎9．定义在上的函数如果对任意给定的等比数列仍是等比数列，称为“保等比数列函数”，现有定义在上的如下函数：‎ ‎①②③④，则其中是“保等比数列函数”的的序号为( )‎ A．①② B．③④ C．①③ D．②④‎ ‎10．等差数列的公差，且，当时，数列的前项和取得最小值，则首项的取值范围为( )‎ A． B．［］ C．［－］ D．[来源:学&科&网Z&X&X&K]‎ 二、填空题(每小题5分，共计25分)‎ ‎11、计算定积分 ‎ ‎12、在△ABC中，M是边BC上的点，N为AM中点，则 ‎ ‎13、设等比数列的前项和为，则＝ ‎ ‎14、已知函数若则实数的最小值为 ‎ ‎15、某同学在研究函数的性质时，得到如下的结论：‎ ‎①的单调递减区间是；‎ ‎②无最小值，无最大值 ‎③的图象与它在（0，0）处切线有两个交点 ‎④的图象与直线有两个交点 其中正确结论的序号是 ‎ 三．解答题。（本题共6小题，共75分）‎ ‎16、(本小题满分12分)‎ ‎ 在平面直角坐标系中，已知点A（－1，－2），B（2，3），C（－2，－1）。‎ ‎(1)求以线段AB、AC为邻边的平行四边形的两条对角线的长 ‎(2)设实数满足，求的值 ‎17.（本小题满分12分）‎ 已知三角形的三内角A、B、C所对边的长分别为、、，设向量，若。‎ ‎(1)求角B的大小；‎ ‎(2)若△ABC的面积为，求AC边的最小值，并指明此时三角形的形状。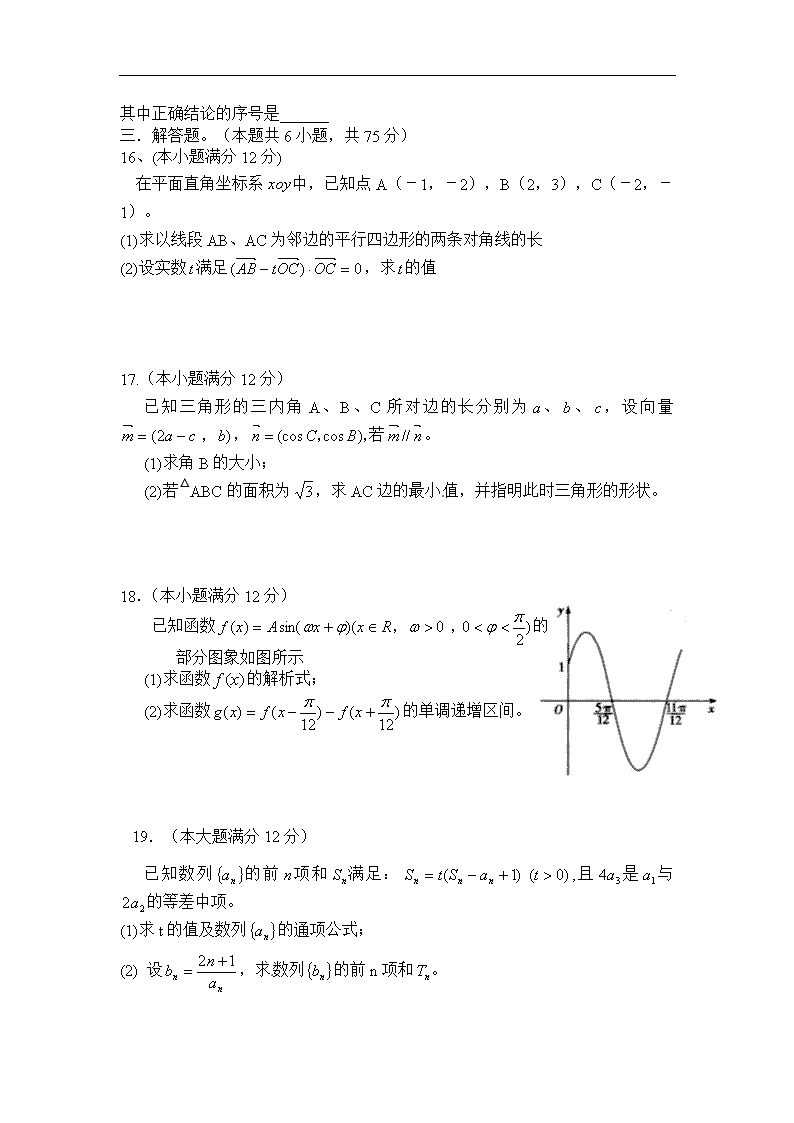‎ ‎18．（本小题满分12分）‎ 已知函数的 部分图象如图所示 ‎(1)求函数的解析式；‎ ‎(2)求函数的单调递增区间。‎ ‎19．（本大题满分12分）‎ 已知数列的前项和满足：且是与的等差中项。‎ ‎(1)求t的值及数列的通项公式；‎ ‎(2) 设，求数列的前n项和。‎ ‎20．（本小题满分13分）‎ 已知函数 ‎(1)若曲线与曲线在它们的交点(1，c)处具有公共切线，求，的值；‎ ‎(2)当时，求函数的单调区间，并求其在区间上的最大值。‎ ‎21．（本小题满分14分）‎ ‎ 已知函数 ‎(1)当时，求函数在上的极值；‎ ‎(2)证明：当x＞0时，；‎ ‎(3)证明：，其中为自然对数的底数）‎ 数学(理科)参考答案 一、选择题(本大题共10小题，每小题5分，共50分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A[来源:学科网ZXXK]‎ A C B A B D[来源:学科网ZXXK]‎ C C C 二、填空题(本大题共5小题，每小题5分，共25分)‎ ‎11、 12、 13、－2012 14、3 15、①④‎ 三、解答题(本大题共6小题，共75分)‎ ‎16、(本题满分12分)‎ 解析(1)由题设知，则所以故所求的两条对角线的长分别为.…………………6分 ‎(2)由题设知 从而，所以.……………………………………………………12分 ‎17、(本小题满分12分)‎ 解：(1)‎ ‎ ‎ 由正弦定理得：‎ 整理得：‎ ‎ 即 ‎ ……………………………………6分 ‎(2)由已知得：‎ 由余弦定理，‎ 当且仅当“”时，上式取等号。‎ 的最小值为2，此时三角形为等边三角形。………………………………12分 ‎18、(本题满分12分)‎ 解析(Ⅰ)由题设图象知，周期，所以，因为点在函数图象上，所以，即 又因为所以，从而，即 又点（0，1）在函数图象上，所以，得A=2.‎ 故函数的解析式为………………………………………………6分 ‎(Ⅱ)‎ ‎＝‎ ‎＝‎ ‎＝‎ ‎＝‎ 由，得 所以函数的单调递增区间是…………………………………………12分 ‎19、(本题满分12分)‎ 解(Ⅰ)当时，，所以，‎ 当时， ①‎ ‎ ， ②‎ ‎①－②，得，即 故是首项，公比等于的等比数列，所以………………4分 故 由是与的等差中项，可得即 因，整理，得，即，‎ 解得或（舍去），所以，故…………6分 ‎(Ⅱ)由(Ⅰ)，得，‎ 所以， ③‎ ‎， ④‎ ‎③－④，得 ……………………8分 ‎＝11分 所以.…………12分 ‎20、(本题满分13分)‎ 解析(Ⅰ)‎ 因为曲线与曲线在它们的交点处具有公共切线，‎ 所以且 即且 解得………………………………………………6分 ‎(Ⅱ)记当时，‎ 令得 时，与的情况如下：‎ ‎[来源:学.科.网]‎ ‎＋‎ ‎0‎ ‎0‎ ‎+‎ 所以函数的音调递增区间为和；单调递减区间为 当即时，函数在区间上单调递增，在区间上的最大值为 当，且，即时，‎ 函数在区间内单调递增，在区间上单调递减，在区间上的最大值为 当，即时，‎ 函数在区间内单调递增，在区间内单调递减，在区间上单调递增，又因 所以在区间上的最大值为……………………………………13分 ‎21、（本题满分14分）[来源:学+科+网]‎ ‎、‎