- 850.00 KB
- 2021-06-20 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
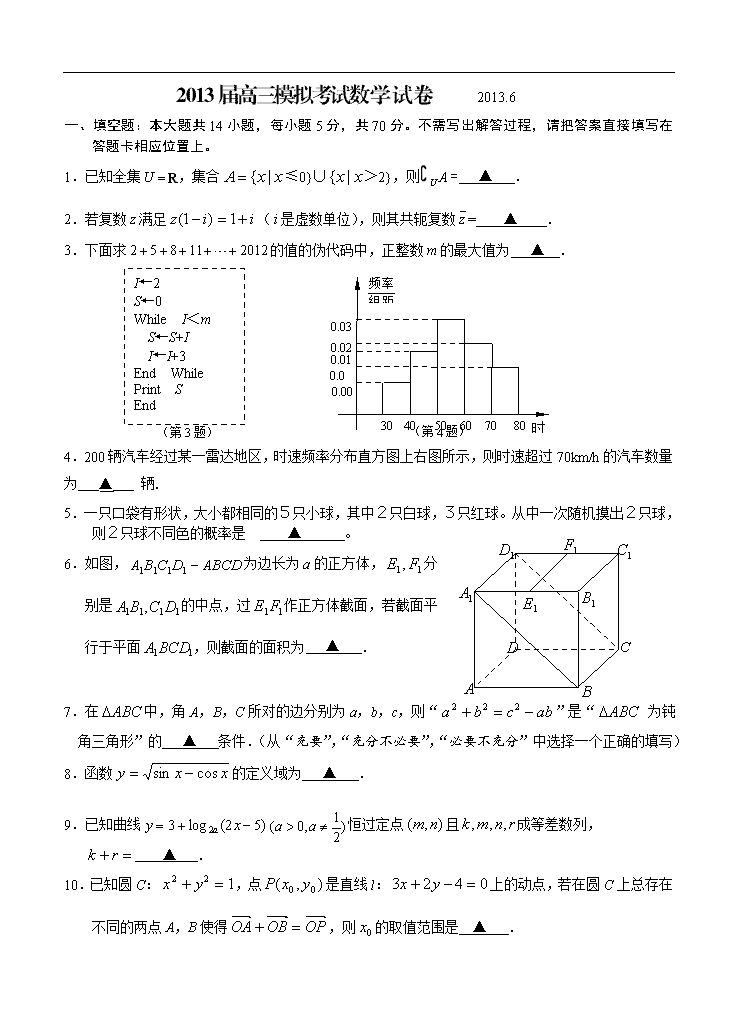
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2013届高三模拟考试数学试卷 2013.6
YCY
一、填空题:本大题共14小题,每小题5分,共70分。不需写出解答过程,请把答案直接填写在答题卡相应位置上。
1.已知全集R,集合≤0}∪>2},则A = ▲ .
2.若复数满足(是虚数单位),则其共轭复数= _ ▲ .
I←2
S←0
While I<m
S←S+I
I←I+3
End While
Print S
End
时速
30
80
70
60
50
40
0.039
0.028
0.018
0.01
0.005
3.下面求的值的伪代码中,正整数的最大值为 ▲ .
(第4题)
(第3题)
4.200辆汽车经过某一雷达地区,时速频率分布直方图上右图所示,则时速超过70km/h的汽车数量为___▲___ 辆.
5.一只口袋有形状,大小都相同的5只小球,其中2只白球,3只红球。从中一次随机摸出2只球,则2只球不同色的概率是 ▲ 。
6.如图,为边长为a的正方体,分
别是的中点,过作正方体截面,若截面平
行于平面,则截面的面积为 ▲ .
7.在中,角A,B,C所对的边分别为a,b,c,则“”是“ 为钝角三角形”的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写)
8.函数的定义域为 ▲ .
9.已知曲线恒过定点且成等差数列,
▲ .
10.已知圆C:,点是直线l:上的动点,若在圆C上总存在不同的两点A,B使得,则的取值范围是 ▲ .
11.已知函数,若函数有两个不同的零点,则的取值范围为___▲ ___.
12.在平面直角坐标系xOy中,对任意的实数m,集合A中的点(x,y)都不
在直线2mx+(1-m2)y-4m-2=0上,则集合A所对应的平面图形面积
的最大值为 ▲ .
13.设函数的定义域为,如果,使(为常数)成立,则称函数在上的均值为,已知四个函数:①;②;③;④,上述四个函数中,满足所在定义域上“均值”为1的函数是 ▲
14.设实数,满足,则的取值范围是 ▲
二、解答题:本大题共6小题,共90分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
15.(本题满分14分)设函数ab,向量a =,
b =,其中角的顶点与坐标原点重合,始边与轴非负半轴重合,终边经过点,且0≤≤.
(1)若点的坐标为,求的值;
(2)若点为平面区域上的一个动点,试确定的取值范围,并求
A
B
C
D
E
F
16.(本题满分14分)如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB=EF.
(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
17.(本题满分14分)交管部门遵循公交优先的原则,在某路段开设了一条仅供车身长为10的公共汽车行驶的专用车道,据交管部门收集的大量数据分析发现,该车道上行驶着的前,后亮亮公共汽车间的安全距离()与车速()之间满足二次函数关系,现已知车速为15时,安全距离为8,车速为45时,安全距离为38;出现堵车状况时,两车安全距离为2
(1)试确定关于的函数关系式;
(2)车速()为多少时,单位时段内通过这条车道的公共汽车数量最多,最多是多少辆?
18.(本题满分16分)设椭圆方程,离心率为,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
(1)求该椭圆的标准方程;
(2)设动点满足,其中M,N是椭圆C上的点,直线OM与ON的斜率之积为,求证:为定值.
19.(本题满分16分)已知数列中,,,为正整数.
(1)证明:数列为等比数列;
(2)设,,若数列的前项之和,并求使的的最小值.
20.(本小题满分16分) 已知函数,.
(1)若函数在其定义域内是单调增函数,求实数的取值范围;
(2)若函数的图象被点分成的两部分为(点除外),该函数图象在点处的切线为,求证:当时,分别完全位于直线的两侧.
(3)试确定的取值范围,使得曲线上存在唯一的点,曲线在该点处的切线与曲线只有一个公共点.
加 试 题
考试时间30分钟;满分40分
21.(本题共2小题;每题10分,共20分)
B.(选修4--2:矩阵与变换)在军事密码学中,发送密码时,先将英文字母数学化,对应如下表:
a
b
c
d
…
z
1
2
3
4
…
26
如果已发现发送方传出的密码矩阵为,双方约定人可逆矩阵为,
试破解发送的英文字母密码.
C.(选修4--4:坐标系与参数方程)在直角坐标系xoy中,曲线M的参数方程为
(为参数),若以该直角坐标系的原点O为极点,轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为:(其中为常数).
(1)求曲线M的普通方程;
(2)若曲线N与曲线M只有一个公共点,求的取值范围.
22.(本小题满分10分)在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD, EF // AB,∠BAF=90º, AD= 2,AB=AF=2EF =1,点P在棱DF上.
(1)若P是DF的中点, 求异面直线BE与CP所成角的余弦值;
(2)若二面角D-AP-C的余弦值为,求PF的长度.
23.(本小题满分10分)设是定义在R上的函数,
(1)若,求g(x);
(2)若,求g(x).
2013届高三模拟考试数学试卷答案 2013.6
YCY
一、填空题:
1.答案: 2.答案:-i 3.答案:2015 4.答案:20;
5.答案:,由A{-1,0,1,2}得A的个数为,其中单元集有4个;
6.答案:,截面与侧面相交于EF,E、F分别是的中点,
7.答案:必要不充分,由得∠C=,故为钝角三角形,反之,
为钝角三角形不只有
8.答案:
9.答案:6,曲线恒过定点,由成等差数列,所以
10.答案:,因OAPB是棱形,故AB垂直平分OP,则当时,不存在,这时当时,,且直线AB过点,
直线AB方程为,圆心到直线AB的距离,
即,且,化为,
11.答案:或;
由图象可得或
12.答案:;利用≥,
得,,
13.答案:-4令,,,,再令,,则是偶函数,先考虑(0,3],利用二分法解决,关键是(0,]上的交点个数的判定,<0,,
,在(0,]上有两个交点,在(,3]上有2个交点,共有4个,在上有8个交点,其和为零,故答案是-4
14.答案:;依题意由,,使,设,则有,,所以,令,则由,求得,所以函数在上单调递减,在上单调递增,于是.
二、解答题:
15.解: (1) 由 且0≤≤得;-------------------------------2分
ab =
x+y-1=0
x
y
0
1
1
-------------- 6分
(2) 如图,作出平面区域
由图形可得 ------------8分
因为 所以
故的最小值 ; 的最大值----------14分
16.(1)证明:设AC与BD的交于O,连结EO,
在正方形ABCD中,BO=AB,∵AB=EF,∴BO=EF,-----2分
又∵EF∥BD,∴EFBO是平行四边形,----------------------------------4分
∵BF∥EO,BF平面ACE,EO平面ACE
∴BF∥平面ACE ---------------------------------------------------------7分
(2)在正方形ABCD中,AC⊥BD,
又∵正方形ABCD和三角形ACE所在的平面互相垂直,
BD平面ABCD,平面ABCD∩平面ACE=AC,
∴BD⊥平面ACE, ---------------------------------------------------10分
∵EO平面ACE
∴BD⊥EO, -------------------------------------------------------------12分
∵EO∥BF,
∴BF⊥BD -------------------------------------------------------------14分
17.解(1)不妨设,依题意,
且
由,---------------------------------3分
若三条道路建设的费用相同,
则
所以,,所以,,-------------------------------------5分
由两倍角的正切公式得,
即---------------------------------------------6分
答:该文化中心建在离N村的距离为km;------------------------7分
(2)总费用,,
即---------------------------------------------------9分
,得,------------------------11分
当时,当时,
所以,当时,有最小值,
这时,,-----------------------13分
答:该文化中心建在离N村的距离为km.-------------------14分
(本题可建立直角坐标系用解析法来解决)
17.(备用题)分析:(1)--4分
(2) -------------------------------8分
(3)分层抽样的比例为2:5:3:7:3,现共抽取20人,在,
在.共有10种可能结果.列举为:
---------------------------------------12分
满足条件的结果有:,
设满足的事件为A,则-------------------14分
18.解:(1)因为,即,---------------------------------2分
∵过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
∴由椭圆的对称性知,椭圆过点,即--------------------4分
,解得,
椭圆方程为 ------------------------------------------------------------7分
(2)证明:设,,
则,化简为 ----------------------9分
∵M,N是椭圆C上的点,∴,
由得-----------------------------------------11分
所以
(定值)------------------------------------------------------16分
19.解析:(1)由条件an+1=2an2+2an,得2an+1+1=4an2+4an+1=(2an+1)2.
∵lg(2a1+1)=lg3≠0,--------------------------------------------------------3分
∴=2.
∴{lg(2an+1)}为等比数列.------------------------------------------------7分
(2)∵lg(2a1+1)=lg3,∴lg(2an+1)=2n-1×lg3,
∴2an+1=3,∴an=(3-1).------------------------------------9分
∵lgTn=lg(2a1+1)+lg(2a2+1)+…+lg(2an+1)=(2n-1)lg3.
∴Tn=3.----------------------------------------------------------------11分
===2-,
∴Sn=2n-
=2n-2+ ----------------------------------------------13分
由Sn>2014得2n-2+>2014,n+>1008,
当n1007时,n+<1008,
当n≥1008时,n+>1008,
∴n的最小值为1008.-------------------------------------------------------16分
20.解析:(1),------------2分
只需要,即,
所以.------------------------------------------------------------------------4分
(2)证明:因为.
所以切线的方程为.--------------------------------------------6分
令,则.
≥0,------------- --------------------------8分
是单调增函数,
当时,;
当时,,
所以分别完全位于直线的两侧.--------------------------10分
(3)设点,
则曲线在点处的切线为
令,则
,,
,
①当时
在上单调递增,在上单调递减
只有唯一解,而是任意选取的值,故不满足题意;----12分
②当时
,记,则.
(i)若,则在上单调递减,在上单调递增
,在上单调递增
只有唯一解
(ii)若 ,则
在上单调递减,在上单调递增
此时存在,使得
在和上单调递增,在上单调递减
此时存在,使得,有两个零点.
(iii)若
则
在上单调递减,在上单调递增
此时存在,使得
在和上单调递增,在上单调递减
此时存在,使得,有两个零点.
综上所述,当时,曲线上存在唯一的点,曲线在该点处的切线与曲线只有一个公共点.----------------------------16分
加 试 题
考试时间30分钟;满分40分
21.
B.令,则A=,
由题意AX=X==B, ----------------------------------5分
故=,
发送方所传出的密码对应的数字是4、5、19、11,
故破解发送的密码是desk. ------------------------------------------------10分
(此题也可以用待定系数法求解)
C.(1)----------------2分
得普通方程为(|x|≤)-----------------------------------5分
(2)曲线M是抛物线的一部分;
对于曲线N,化成直角坐标方程为,曲线N是一条直线,
若曲线M,N只有一个公共点,则有直线N过点时满足要求,并且向左下方平行运动直到过点(-,1)之前总是保持只有一个公共点,再接着向左下方平行运动直到相切之前总是有两个公共点,所以-+1<t≤+1满足要求,-----8分
相切时仍然只有一个公共点,由t-x=x2-1,得x2+x-1-t=0,
,得,
的取值范围为-+1<t≤+1或-------------------------------10分
22.(1)因为∠BAF=90º,所以AF⊥AB,
因为 平面ABEF⊥平面ABCD,且平面ABEF ∩平面ABCD= AB,
所以AF⊥平面ABCD,因为四边形ABCD为矩形,
所以以A为坐标原点,AB,AD,AF分别
为x,y,z轴,建立如图所示空间直角坐标系.
所以 ,,,.所以 ,
,所以,
即异面直线BE与CP所成角的余弦值为.------------------------------5分
(2)解:因为AB⊥平面ADF,所以平面APF的法向量为.
设P点坐标为,在平面APC中,,,
所以 平面APC的法向量为,
所以 ,
解得,或(舍). 所以.--------------------------10分
23.解(1)若,则,
所以
---------------------------------------------------------------------3分
又无意义,即R,且)---------------------------5分
(2)若,则
所以
因为--------------8分
所以
所以R,且)-----------------------------------------10分
相关文档
- 衢州二中 2019 学年第二学期线上教2021-06-194页
- 湘豫名校2021届高三8月联考高三数2021-06-1621页
- 安徽省安庆市桐城市2020高三数学试2021-06-159页
- 安徽省安庆市桐城市2020高三数学试2021-06-159页
- 甘肃省陇南市6月联考2020届高三数2021-06-1122页
- 上海市进才中学2020-2021学年第一2021-06-119页
- 江苏省南通市海门市第一中学2021届2021-06-107页
- 高三数学试卷2021-06-1010页
- 2021湖北龙泉中学、荆州中学、宜昌2021-06-108页
- 2021湖北龙泉中学、荆州中学、宜昌2021-05-2611页