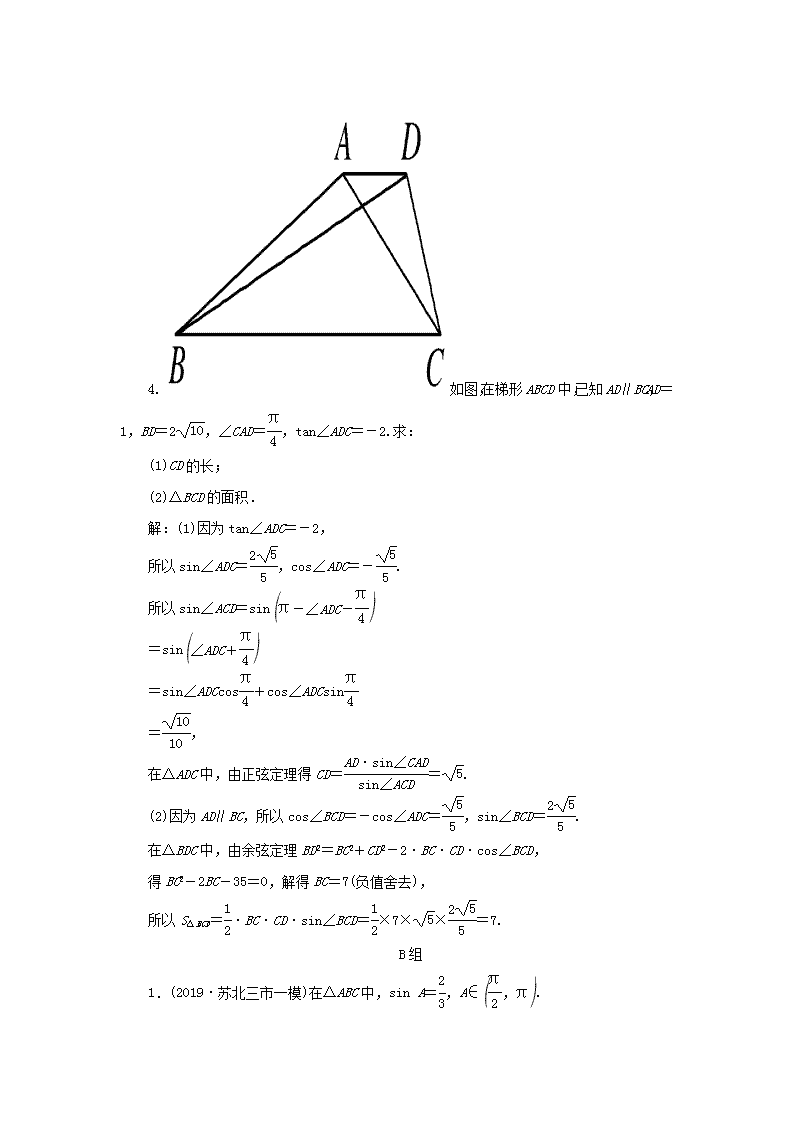2020届江苏省高考数学二轮复习课时达标训练（三）解三角形 6页

课时达标训练(三) 解三角形 A组 ‎1．(2019·南京三模)已知a，b，c分别是△ABC三个角A，B，C所对的边，且满足acos B＋bcos A＝.‎ ‎(1)求证：A＝C；‎ ‎(2)若b＝2，·＝1，求sin B的值．‎ 解：(1)证明：由正弦定理，得sin Acos B＋sin Bcos A＝，‎ 即(sin Acos B＋sin Bcos A)cos C＝sin(A＋B)cos C＝sin Ccos A.‎ 因为A＋B＝π－C，所以sin(A＋B)＝sin C，‎ 所以sin Ccos C＝sin Ccos A.‎ 因为C是△ABC的内角，所以sin C≠0，所以cos C＝cos A.‎ 又A，C是△ABC的内角，所以A＝C.‎ ‎(2)由(1)知，A＝C，所以a＝c，所以cos B＝＝.‎ 因为·＝1，所以a2cos B＝a2－2＝1，所以a2＝3.‎ 所以cos B＝.‎ 又B∈(0，π)，所以sin B＝ ＝.‎ ‎2．(2019·无锡期末)在△ABC中，设a，b，c分别是角A，B，C的对边，已知向量m＝(a，sin C－sin B)，n＝(b＋c，sin A＋sin B)，且m∥n.‎ ‎(1)求角C的大小；‎ ‎(2)若c＝3，求△ABC周长的取值范围．‎ 解：(1)由m∥n及m＝(a，sin C－sin B)，n＝(b＋c，sin A＋sin B)得a(sin A＋sin B)－(b＋c)(sin C－sin B)＝0.‎ 由正弦定理，得a(a＋b)－(b＋c)(c－b)＝0，‎ 所以a2＋ab－(c2－b2)＝0，得c2＝a2＋b2＋ab.‎ 又c2＝a2＋b2－2abcos C，‎ 所以a2＋b2＋ab＝a2＋b2－2abcos C，‎ 所以ab＝－2abcos C.‎ 因为ab＞0，所以cos C＝－.‎ 又C∈(0，π)，所以C＝.‎ ‎(2)在△ABC中，c2＝a2＋b2－2abcos C，‎ 所以a2＋b2－2abcos＝9，即(a＋b)2－ab＝9，‎ 所以ab＝(a＋b)2－9≤，所以≤9，‎ 即(a＋b)2≤12，所以a＋b≤2，当且仅当a＝b时取等号．‎ 又a＋b＞c，所以6＜a＋b＋c≤2＋3，‎ 所以△ABC周长的取值范围是(6，3＋2]．‎ ‎3．(2018·盐城三模)在△ABC中，角A，B，C的对边分别为a，b，c，AD为边BC上的中线．‎ ‎(1)若a＝4，b＝2，AD＝1，求边c的长；‎ ‎(2)若·＝c2，求角B的大小．‎ 解：(1)在△ADC中，因为AD＝1，AC＝2，DC＝BC＝2，‎ 由余弦定理得cos C＝＝＝.‎ 故在△ABC中，由余弦定理，得c2＝a2＋b2－2abcos C＝42＋22－2×4×2×＝6，所以c＝.‎ ‎(2)因为AD为边BC上的中线，‎ 所以＝(＋)，‎ 所以c2＝·＝2＋·＝c2＋cbcos A，‎ ‎∴c＝bcos A.‎ ‎∴AB⊥BC，∴B＝90°.‎ ‎4.如图，在梯形ABCD中，已知AD∥BC，AD＝1，BD＝2，∠CAD＝，tan∠ADC＝－2.求：‎ ‎(1)CD的长；‎ ‎(2)△BCD的面积．‎ 解：(1)因为tan∠ADC＝－2，‎ 所以sin∠ADC＝，cos∠ADC＝－.‎ 所以sin∠ACD＝sin ‎＝sin ‎＝sin∠ADCcos＋cos∠ADCsin ‎＝，‎ 在△ADC中，由正弦定理得CD＝＝.‎ ‎(2)因为AD∥BC，所以cos∠BCD＝－cos∠ADC＝，sin∠BCD＝.‎ 在△BDC中，由余弦定理BD2＝BC2＋CD2－2·BC·CD·cos∠BCD，‎ 得BC2－2BC－35＝0，解得BC＝7(负值舍去)，‎ 所以S△BCD＝·BC·CD·sin∠BCD＝×7××＝7.‎ B组 ‎1．(2019·苏北三市一模)在△ABC中，sin A＝，A∈.‎ ‎(1)求sin 2A的值；‎ ‎(2)若sin B＝，求cos C的值．‎ 解：(1)由sin A＝，A∈，得 cos A＝－＝－ ＝－，‎ 所以sin 2A＝2sin Acos A＝－.‎ ‎(2)由A∈，得B为锐角，‎ 又sin B＝，所以cos B＝ ＝，‎ 所以cos C＝－cos(A＋B)＝－(cos Acos B－sin Asin B)‎ ‎＝－＝.‎ ‎2．(2018·全国卷Ⅰ)在平面四边形ABCD中，∠ADC＝90°，∠A＝45°，AB＝2，BD＝5.‎ ‎(1)求cos ∠ADB；‎ ‎(2)若DC＝2，求BC.‎ 解：(1)在△ABD中，由正弦定理得＝，‎ 即＝，‎ 所以sin ∠ADB＝.‎ 由题设知，∠ADB<90°，‎ 所以cos ∠ADB＝ ＝.‎ ‎(2)由题设及(1)知，‎ cos ∠BDC＝sin ∠ADB＝.‎ 在△BCD中，由余弦定理得 BC2＝BD2＋DC2－2BD·DC·cos ∠BDC ‎＝25＋8－2×5×2×＝25，‎ 所以BC＝5.‎ ‎3．(2019·南通等七市一模)在△ABC中，a，b，c分别为角A，B，C所对边的长，acos ‎ B＝bcos A，cos A＝.‎ ‎(1)求角B的大小；‎ ‎(2)若a＝，求△ABC的面积．‎ 解：(1)在△ABC中，因为cos A＝，0＜A＜π，‎ 所以sin A＝＝.‎ 由acos B＝bcos A及正弦定理＝，‎ 得sin Acos B＝sin Bcos A，‎ 所以cos B＝sin B.‎ 若cos B＝0，则sin B＝0，与sin2B＋cos2B＝1矛盾，故cos B≠0.‎ 于是tan B＝＝1.‎ 又0＜B＜π，所以B＝.‎ ‎(2)由(1)及正弦定理＝，得＝，‎ 所以b＝.‎ 又sin C＝sin(π－A－B)＝sin(A＋B)＝sin Acos B＋cos Asin B＝×＋×＝，‎ 所以△ABC的面积S＝absin C＝×××＝.‎ ‎4．在锐角△ABC中，内角A，B，C的对边分别为a，b，c，已知2acos B＝2c－b.‎ ‎(1)若cos(A＋C)＝－，求cos C的值；‎ ‎(2)若b＝5，·＝－5，求△ABC的面积；‎ ‎(3)若O是△ABC外接圆的圆心，且·＋·＝m，求m的值．‎ 解：由2acos B＝2c－b，得2sin Acos B＝2sin C－sin B，‎ 即2sin Acos B＝2sin(A＋B)－sin B，‎ 化简得cos A＝，则A＝60°.‎ ‎(1)由cos(A＋C)＝－cos B＝－，‎ 得cos B＝，所以sin B＝.‎ 所以cos C＝cos(120°－B)＝－cos B＋sin B＝.‎ ‎(2)因为·＝·(－)＝·－2＝||·||·cos A－||2＝bc－b2＝－5，‎ 又b＝5，解得c＝8，‎ 所以△ABC的面积为bcsin A＝10.‎ ‎(3)由·＋·＝m，‎ 可得··＋··＝m2.(*)‎ 因为O是△ABC外接圆的圆心，‎ 所以·＝2，·＝2，‎ 又||＝，‎ 所以(*)可化为·c2＋·b2＝m·，‎ 所以m＝2(cos Bsin C＋sin Bcos C)＝2sin(B＋C)＝2sin A＝.‎