重庆市育才中学2019-2020高二数学下学期期末试题（Word版附答案） 13页

‎[机密]2020年 ‎7月11日前 ‎ 2019—2020学年度(下)高中学业质量调研抽测 ‎ 高二数学试题卷 ‎ 数学试题卷共6页，考试时间120分钟，满分150分。‎ 注意事项：‎ ‎1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎2．作答时，务必将答案写在答题卡上，写在本试卷及草稿纸上无效。‎ ‎3．考试结束后，将本试卷、答题卡一并收回。‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的. 请将正确答案的代号填涂在答题卡上.‎ ‎1.已知为虚数单位，若是纯虚数，则实数的值为 A． B． C． D．‎ ‎2.某物体的运动方程为，其中位移的单位是米，时间的单位是秒，那么该物体在秒时的瞬时速度大小是 ‎ ‎ A．米/秒 B．米/秒 C．米/秒 D．米/秒 ‎ ‎3.的展开式中的常数项为 A． B． C． D． ‎ ‎4. 从名志愿者中选出人分别从事翻译、导游、导购三项不同工作，则选派方案共有 A．种 B．种 C．种 D．种 ‎5.若，则 ‎ A. B. C. D. ‎ ‎6.已知某批零件的长度误差（单位：）服从正态分布，若，，现从中随机抽取一件，其长度误差落在区间内的概率 A. 0.1359 B. 0.2718 C. 0.3174 D. 0.0456‎ 高二数学试题 第13页（共6页）‎ ‎0.02‎ ‎0 1 2 3 4 5 x ‎0.20‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ y(单位:%)‎ ‎0.05‎ ‎0.1‎ ‎0.15‎ ‎0.18‎ ‎7．网络是一种先进的高频传输技术，我国的技术发展迅速，已位居世界前列.华为公司于2019年8月初推出了一款手机，现调查得到该款手机上市时间和市场占有率（单位：%）的几组相关对应数据.如图所示的折线图中，横轴1代表2019年8月，2代表2019年9月……，5代表2019年12月，根据数据得出关于的线性回归方程为.若用此方程分析并预测该款手机市场占有率的变化趋势，则该款手机市场占有率能超过0.5% 的最早时间是（精确到月）‎ A．2020年6月 B．2020年7月 C．2020年8月 D．2020年9月 ‎8. 从,,,,,,中任取两个不同的数，事件“取到的两个数之和为偶数”，‎ 事件“取到的两个数均为偶数”，则 A. B. C. D. ‎ ‎9. 在个排球中有个正品，个次品.从中抽取个，则正品数比次品数少的概率为 A. B. C. D. 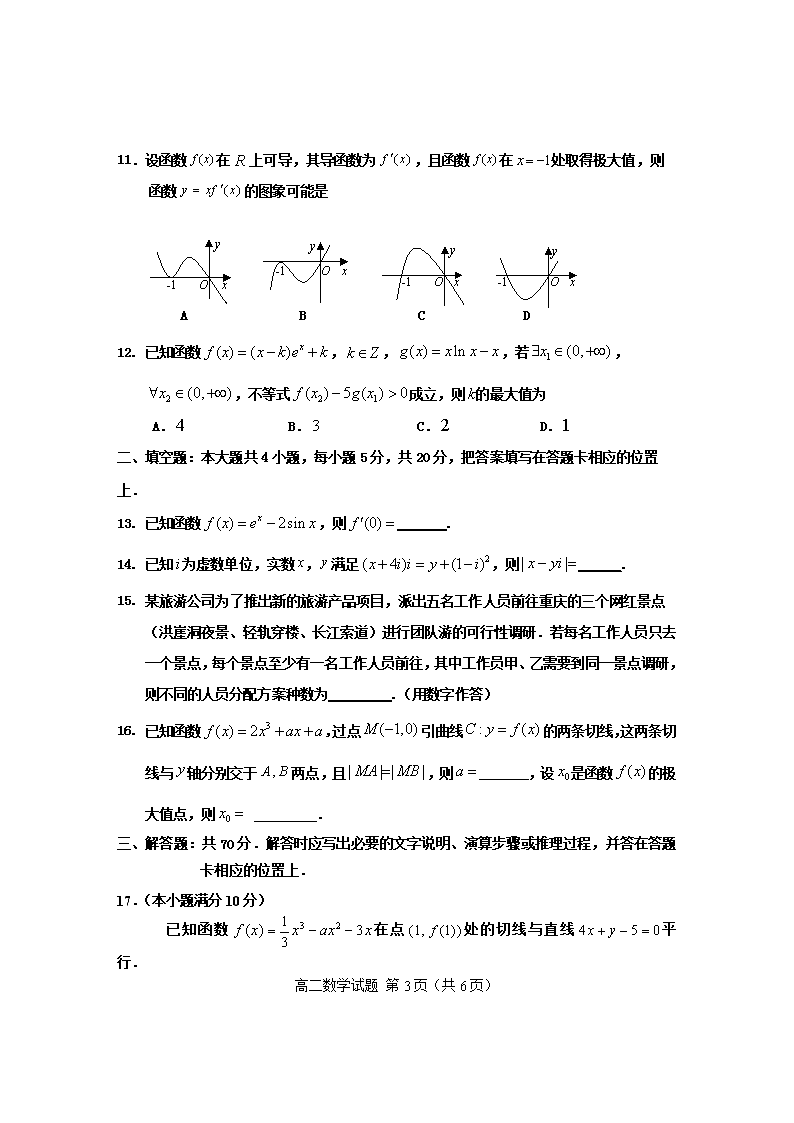‎ A D E B C ‎10．如图所示的五个区域中，中心区域是一幅图画，现要求在其余四个区域中涂色，有四种颜色可供选择，要求每个区域只涂一种颜色且相邻区域所涂颜色不同，则不同的涂色方法种数为 A． B． ‎ C． D．‎ 高二数学试题 第13页（共6页）‎ ‎11．设函数在上可导，其导函数为，且函数在处取得极大值，则 函数的图象可能是 ‎-1 O x y ‎-1 O x y ‎-1 O x y ‎-1 O x y ‎ ‎ ‎ ‎ A B C D ‎ ‎12. 已知函数，，，若，，不等式成立，则的最大值为 A． B．　 C． D． ‎ 二、填空题：本大题共4小题，每小题5分，共20分，把答案填写在答题卡相应的位置上．‎ ‎13. 已知函数，则_______.‎ ‎14. 已知为虚数单位，实数，满足，则______.‎ ‎15. 某旅游公司为了推出新的旅游产品项目，派出五名工作人员前往重庆的三个网红景点 ‎（洪崖洞夜景、轻轨穿楼、长江索道）进行团队游的可行性调研．若每名工作人员只去一个景点，每个景点至少有一名工作人员前往，其中工作员甲、乙需要到同一景点调研，则不同的人员分配方案种数为_________.（用数字作答）‎ ‎16. 已知函数,过点引曲线的两条切线，这两条切线与轴分别交于两点，且，则 ，设是函数的极大值点，则 ． ‎ 三、解答题：共70分．解答时应写出必要的文字说明、演算步骤或推理过程，并答在答题卡相应的位置上． ‎ ‎17．（本小题满分10分）‎ 已知函数在点处的切线与直线平行．‎ 高二数学试题 第13页（共6页）‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）求函数在区间的最大值和最小值．‎ ‎18.（本小题满分12分）‎ 为了调查某社区居民每天参加健身的时间，某机构在该社区随机采访男性、女性各50名，其中每人每天的健身时间不少于1小时称为“健身族”，否则称其为“非健身族”，调查结果如下：‎ 健身族 非健身族 合计 男性 ‎40‎ ‎10‎ ‎50‎ 女性 ‎30‎ ‎20‎ ‎50‎ 合计 ‎70‎ ‎30‎ ‎100‎ ‎（Ⅰ）若居民每人每天的平均键身时间不少于60分钟，则称该社区为“健身社区”.已知被随机采访的男性健身族，男性非健身族，女性健身族，女性非健身族每人每天的平均健身时间分别是1.2小时，0.8小时，1.5小时，0.7小时，试估计该社区可否称为“健身社区”？‎ ‎（Ⅱ）根据以上数据，能否在犯错误的概率不超过的情况下认为“健身族”与“性别”有关？‎ 参考公式：，其中.‎ 参考数据：‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.455‎ ‎0.708‎ ‎1.321‎ ‎3.840‎ ‎5.024‎ ‎6.635‎ 高二数学试题 第13页（共6页）‎ ‎19.（本小题满分12分）‎ 某地盛产脐橙，该地销售脐橙按照等级分为四类：珍品、特级、优级和一级（每箱重量为5kg），某采购商打算在该地采购一批脐橙销往外地，并从采购的这批脐橙中随机抽取50箱，利用脐橙的等级分类标准得到的数据如下表：‎ 等级 珍品 特级 优级 一级 箱数 ‎10‎ ‎15‎ ‎15‎ ‎10‎ ‎（Ⅰ）用分层抽样的方法从这50箱脐橙中抽取10箱，再从抽取的10箱中随机抽取3箱，表示随机抽取的3箱中是特级的箱数，求的分布列及数学期望；‎ ‎（Ⅱ）利用样本估计总体，该地提出两种购销方案供采购商参考:‎ 方案一：不分等级卖出，价格为20元/kg；‎ 方案二：分等级卖出，分等级的脐橙价格如下：‎ 等级 珍品 特级 优级 一级 售价（元/kg）‎ ‎25‎ ‎20‎ ‎15‎ ‎10‎ 从采购商节约资金的角度考虑，应该采用哪种方案？‎ ‎20．（本小题满分12分）‎ 已知函数（为自然对数的底数）．‎ ‎（Ⅰ）当时，求证：；‎ ‎（Ⅱ）设，若关于的不等式对于任意的恒成立，求实数的取值范围．‎ 高二数学试题 第13页（共6页）‎ ‎21. （本小题满分12分）‎ ‎“蛟龙号”载人潜水艇执行某次任务时从海底带回来某种生物.甲、乙两个生物小组分别独立开展对该生物离开恒温箱的成活情况的研究，每次试验一个生物，甲组能使生物成活的概率为，乙组能使生物成活的概率为，假定试验后生物成活，则称该次试验成功，如果生物不成活，则称该次试验失败.‎ ‎（Ⅰ）甲小组做了三次试验，求至少两次试验成功的概率；‎ ‎（Ⅱ）如果乙小组成功了4次才停止试验，求乙小组第四次成功前共有三次失败，且恰有两次连续失败的概率；‎ ‎（Ⅲ）若甲、乙两小组各进行2次试验，记试验成功的总次数为随机变量，求 的分布列与数学期望.‎ ‎22. （本小题满分12分）‎ 已知函数．‎ ‎（Ⅰ）函数在点的切线经过点，求函数的极值；‎ ‎（Ⅱ）若函数在区间上存在零点，求实数的取值范围． ‎ 高二数学试题 第13页（共6页）‎ ‎2019—2020学年度(下)高中学业质量调研抽测 ‎ 高二数学参考答案及评分意见 一、选择题： 1-5：C B A C D ； 6-10：A C D B A ； 11-12:C B. ‎ 二、填空题：13. ； 14. ； 15.； 16. （3分），（2分）‎ 三、解答题： ‎ ‎17.解:（Ⅰ）由，得， ……………………1分 ‎. ……………………………………………………………2分 由题意，得， ∴. …………………………………………4分 ‎（Ⅱ），，‎ 由，得或，‎ 由，得， …………………………………………6分 ‎∵，‎ ‎∴的单调递增区间为，，递减区间为.‎ ‎∴的极大值为，极小值为. ……………………………8分 高二数学试题 第13页（共6页）‎ 又，，‎ ‎∴函数在区间的最大值为，最小值为． ……………………10分 ‎18.解（Ⅰ）随机抽样的100名居民每人每天的平均健身时间为 小时， ……………………………4分 由此估计该小区居民每人每天的平均健身时间为1.15小时，‎ 因为1.15小时分钟，所以该社区可称为“健身社区”. ……………………6分 ‎（Ⅱ）由联立表可得，‎ ‎. ………10分 ‎∵，‎ 所以能在犯错误概率不超过的情况下认为“健康族”与“性别”有关. ……………12分 ‎19.解：（Ⅰ）用分层抽样的方法从这50箱脐橙中抽取10箱，其中特级品为箱,非特级品为箱,…1分 表示随机抽取的是特级的箱数，则的取值为. ………………………2分 则 ， ，‎ 高二数学试题 第13页（共6页）‎ ‎ ， . ‎ 的分布列为：‎ ‎……………………………………………6分 ‎. …………………………………………8分 ‎（Ⅱ）设方案二的单价为，则 的期望为：‎ ‎. …………………………………………11分 ‎ ,从采购商的角度考虑，应该采用方案二. …………………………………12分 ‎20．解：（Ⅰ）由，∵， ‎ ‎∴. …………………………………………………2分 ‎∴在上单调递增， …………………………………………………3分 ‎∴． …………………………………………………4‎ 高二数学试题 第13页（共6页）‎ 分 ‎（Ⅱ）由，得.‎ ‎∵在上恒成立，‎ ‎ 即在上恒成立. …………………………………6分 当时，设， ‎ ‎. ……………………………7分 由（Ⅰ）知在上恒成立，‎ 令得，∴当时，，单调递减，‎ 当时，，单调递增， ………………………………………9分 ‎∴. ……………………………………………………………11分 ‎∴. ……………………………………………………………12分 ‎21.解：（Ⅰ）记至少两次试验成功为事件A，则， ‎ ‎∴甲小组做三次试验，至少两次试验成功的概率为 高二数学试题 第13页（共6页）‎ ‎. …………………………3分 ‎（Ⅱ）由题意知，乙小组第四次成功前共进行了6次试验，‎ 其中三次成功三次失败，且恰有两次连续失败，共有种情况. ‎ 记乙小组第四次成功前共有三次失败，且恰有两次连续失败为事件B，‎ 则，‎ ‎∴乙小组第四次成功前共有三次失败，且恰有两次连续失败的概率为. …………………6分 ‎（Ⅲ）X的所有可能取值为0，1，2，3，4. 则，‎ ‎，‎ ‎，‎ ‎， ， ‎ ‎∴X的概率分布为：‎ X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎………………………………………………11分 ‎∴数学期望 高二数学试题 第13页（共6页）‎ ‎. …………………12分 ‎22.解：（Ⅰ）由函数，，，‎ ‎， . ‎ 在点的切线方程为，代入点 得. ……………3分 ‎，得，‎ 当时，，单调递减，‎ 当时，，单调递增，‎ 的极小值为. ……………………………………5分 ‎（Ⅱ），‎ 令，因为，‎ 当 时，，所以，‎ 所以在上为增函数，则. …………………7分 当时，，所以，所以在上为增函数，‎ 则，所以在上没有零点. ………………………8分 高二数学试题 第13页（共6页）‎ 当时，即，因为在上为增函数，则存在唯一的，‎ 使得，且当时，，当时，. ‎ 所以，当时，，为减函数，‎ 当时，，为增函数，‎ 当时，， ………………………………………11分 因为，当趋于时，趋于，‎ 所以在内，一定存在一个零点.，所以． …………………12分 高二数学试题 第13页（共6页）‎