高中数学必修2教案：第一章《立体几何初步》单元知识总结 4页

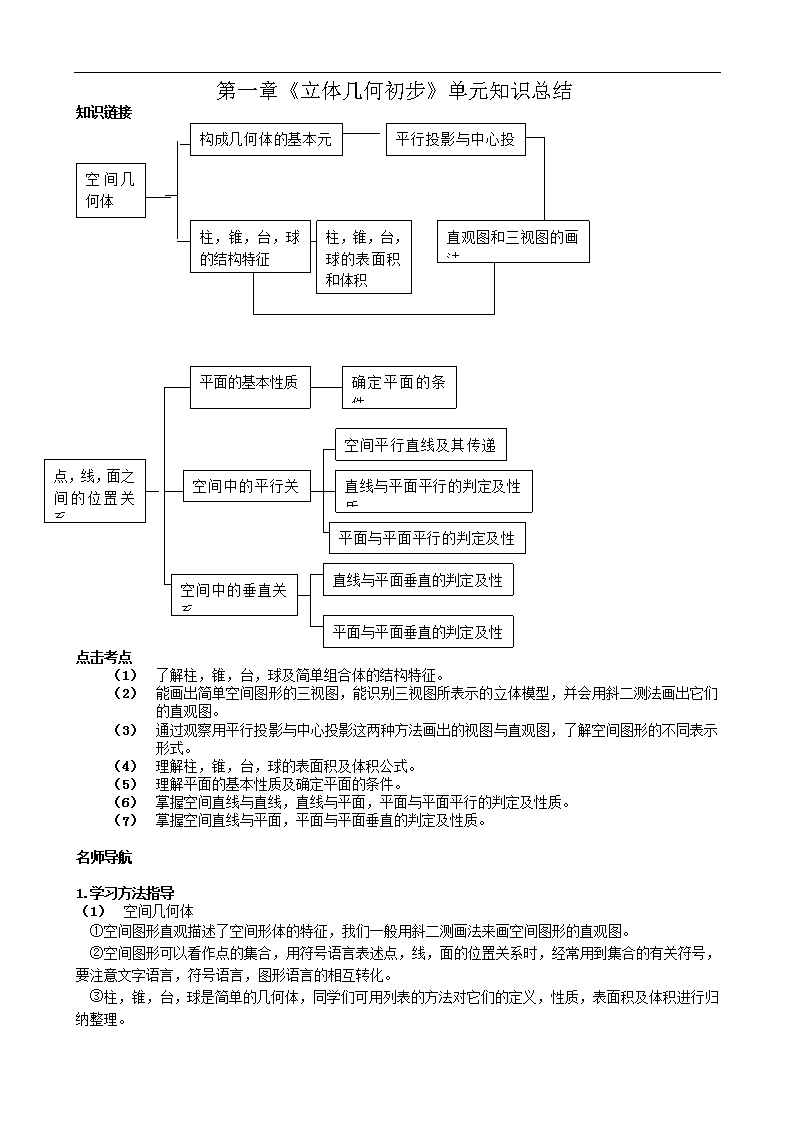
第一章《立体几何初步》单元知识总结 知识链接 空间几何体 构成几何体的基本元素 平行投影与中心投影 ‎ ‎ ‎ ‎ ‎ ‎ 柱，锥，台，球的表面积和体积 柱，锥，台，球的结构特征 直观图和三视图的画法 ‎ ‎ 确定平面的条件 平面的基本性质 空间平行直线及其传递性 点，线，面之间的位置关系 直线与平面平行的判定及性质 空间中的平行关系 平面与平面平行的判定及性质 直线与平面垂直的判定及性质 空间中的垂直关系 平面与平面垂直的判定及性质 点击考点 （1） 了解柱，锥，台，球及简单组合体的结构特征。‎ （2） 能画出简单空间图形的三视图，能识别三视图所表示的立体模型，并会用斜二测法画出它们的直观图。‎ （3） 通过观察用平行投影与中心投影这两种方法画出的视图与直观图，了解空间图形的不同表示形式。‎ （4） 理解柱，锥，台，球的表面积及体积公式。‎ （5） 理解平面的基本性质及确定平面的条件。‎ （6） 掌握空间直线与直线，直线与平面，平面与平面平行的判定及性质。‎ （7） 掌握空间直线与平面，平面与平面垂直的判定及性质。‎ 名师导航 ‎1.学习方法指导 （1） 空间几何体 ①空间图形直观描述了空间形体的特征，我们一般用斜二测画法来画空间图形的直观图。‎ ②空间图形可以看作点的集合，用符号语言表述点，线，面的位置关系时，经常用到集合的有关符号，要注意文字语言，符号语言，图形语言的相互转化。‎ ③柱，锥，台，球是简单的几何体，同学们可用列表的方法对它们的定义，性质，表面积及体积进行归纳整理。‎ ④对于一个正棱台，当上底面扩展为下底面的全等形时，就变为一个直棱柱；当上底面收缩为中心点时，就变为一个正棱锥。由和，就可看出它们的侧面积与体积公式的联系。‎ （1） 点，线，面之间的位置关系 ‎ ①“确定平面”是将空间图形问题转化为平面图形问题来解决的重要条件，这种转化最基本的就是三个公理。‎ ‎ ②空间中平行关系之间的转化：直线与直线平行 直线与平面平行 ‎ 平面与平面平行。‎ ‎ ③空间中垂直关系之间的转化：直线与直线垂直 直线与平面垂直 平面与平面垂直。‎ ‎2.思想方法小结 ‎ 在本章中需要用到的数学思想方法有：观察法，数形结合思想，化归与转化思想等。主要是立体几何问题转化为平面几何问题，平行与垂直的相互转化等。‎ ‎3.综合例题分析 例1：如图，P是ABC所在平面外一点，，，分别是，，的重心。‎ （1） 求证：平面平面ABC； P （2） 求：.‎ 证明:(1) 连结,,,设,‎ ‎ ,,则D,E,F分 别是BC,AC,AB的中点,且 ‎ ‎ C ‎ ‎ A ‎ B ‎ ‎ ‎ 所以, ,‎ 且,,‎ 所以 ,‎ 从而, 平面平面ABC.‎ ‎(2) 由平面几何知识有，， ‎ 所以， .‎ 点评: (1)由线线平行 线面平行 面面平行,是证明平行问题的常用方法.‎ ‎(2)灵活运用平面几何知识是解决本题的关键。‎ 例2：试证：正四面体内任意一点到各面距离之和等于这个正四面体的高。‎ 分析：如图，设P为正四面体ABCD内任一点，AO为正四面体 A 的高，点P到各面的距离分别为 则 P ‎ B D ‎ ‎ ‎ C 即 ‎ ‎ 正四面体各面是全等的正三角形 ‎ ‎ ‎ ‎ 点评：多面体问题常用技巧有“割”“补”“等积变换”等，利用这些技巧可使问题化繁为易。‎ 例3：圆台的内切球半径为R，且圆台的全面积和球面积之比为。求圆台的上，下底面半径（）。‎ 解：如图，设圆台母线为， 则，由平面几何知识得，‎ ‎ 即 ‎ 又 ‎ 由题意得， ‎ 即 ‎ ‎ 代入 得 ，，.‎ 点评: (1) 解组合体的关键是注意选择合适的角度画出示意图，通过交点交线来研究问题，正确作出截面，把复杂问题转化为熟悉的,较常见的问题.‎ ‎ (2) 轴截面在解决旋转体问题中，有着相当重要的作用.‎ 例4．已知三棱锥中，，，⊥平面，，‎ 分别是上的动点，且，‎ ‎（Ⅰ）求证：不论为何值，总有平面⊥平面；‎ ‎（Ⅱ）当为何值时，平面⊥平面？‎ ‎ 证（Ⅰ）∵平面，∴，‎ ‎ ∵，且，∴平面，‎ ‎ 又∵（），‎ ‎ ∴不论为何值，恒有，∴平面，平面，‎ ‎ ∴不论为何值恒有平面⊥平面．‎ ‎（Ⅱ）由（Ⅰ）知，，又要平面平面，‎ ‎∴平面，∴，‎ ‎∵，，，‎ ‎∴，‎ ‎∴，由得，‎ ‎∴，‎ 故当时，平面平面．‎ 点评：证明垂直和平行一样，要注意线面与面面的转化及立几与平几的转化。‎ 误区莫入 （1） 几何中的平面是没有厚度且可以无限延展，因此，用平行四边形表示平面时，必要时可以把它延展开来。如同画直线一样，直线是可以无限延展的，但在画直线时，却只画出一条线段来表示。‎ （2） 平面几何中有些概念和性质，推广到空间不一定正确。如：“过直线外一点只能作一条直线与已知直线垂直”在空间就不正确。而有些命题推广到空间还是正确，如：平行线的传递性及关于两角相等的定理等。‎ ‎ ‎