【数学】2018届一轮复习北师大版第七章立体几何第三节空间点直线平面之间的位置关系教案 12页

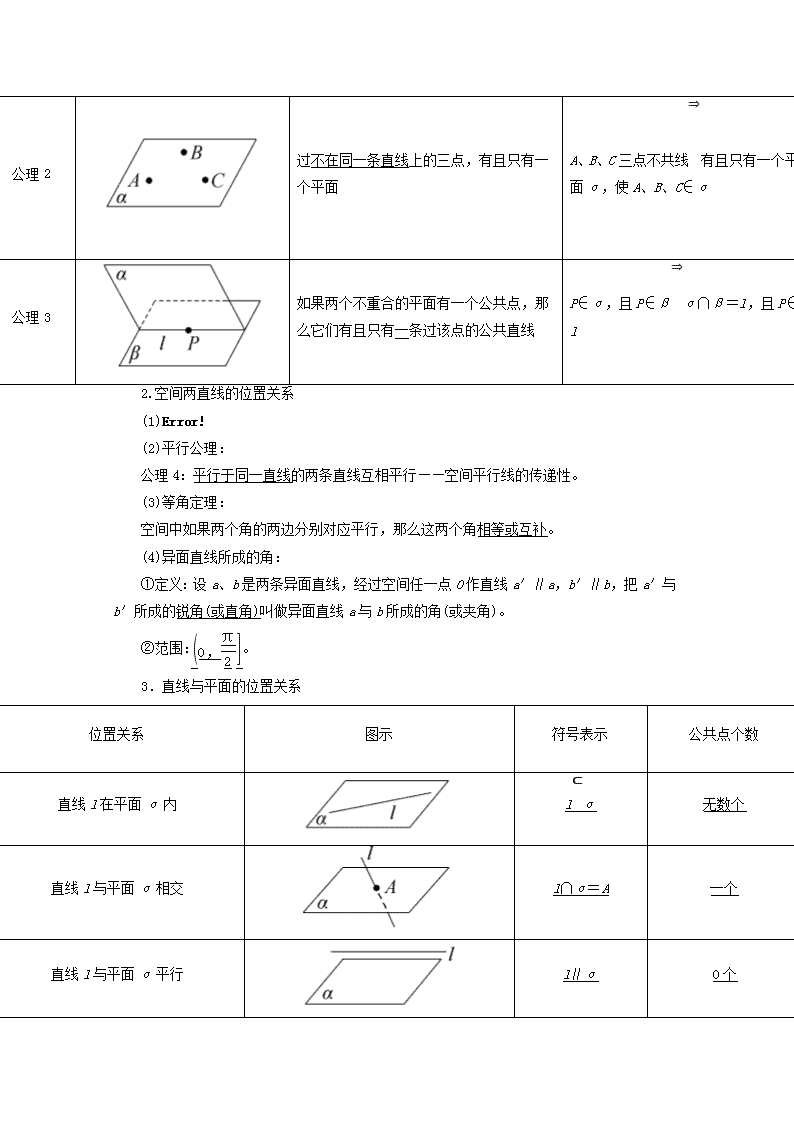
第三节　空间点、直线、平面之间的位置关系 ‎☆☆☆2017考纲考题考情☆☆☆‎ 考纲要求 真题举例 命题角度 ‎　　1.理解空间直线、平面位置关系的定义，并了解作为推理依据的公理和定理；‎ ‎2.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题。‎ ‎2016，山东卷，6,5分(线线、面面位置关系)‎ ‎2015，广东卷，7,5分(线线、面面位置关系)‎ ‎2014，全国卷Ⅱ，11,5分(线面位置关系判定)‎ ‎　　平面的基本性质是立体几何的基础，而两条异面直线所成的角和距离是高考热点，在新课标高考卷中频频出现。‎ 微知识　小题练 自|主|排|查 ‎1．平面的基本性质 名称 图示 文字表示 符号表示 公理1‎ 如果一条直线上的两点在一个平面内，那么这条直线在此平面内 A∈l，B∈l，且A∈α，B∈α⇒l⊂α 公理2‎ 过不在同一条直线上的三点，有且只有一个平面 A、B、C三点不共线⇒有且只有一个平面α，使A、B、C∈α 公理3‎ 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线 P∈α，且P∈β⇒α∩β＝l，且P∈l ‎2.空间两直线的位置关系 ‎(1) ‎(2)平行公理：‎ 公理4：平行于同一直线的两条直线互相平行——空间平行线的传递性。‎ ‎(3)等角定理：‎ 空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。‎ ‎(4)异面直线所成的角：‎ ‎①定义：设a、b是两条异面直线，经过空间任一点O作直线a′∥a，b′∥b，把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)。‎ ‎②范围：。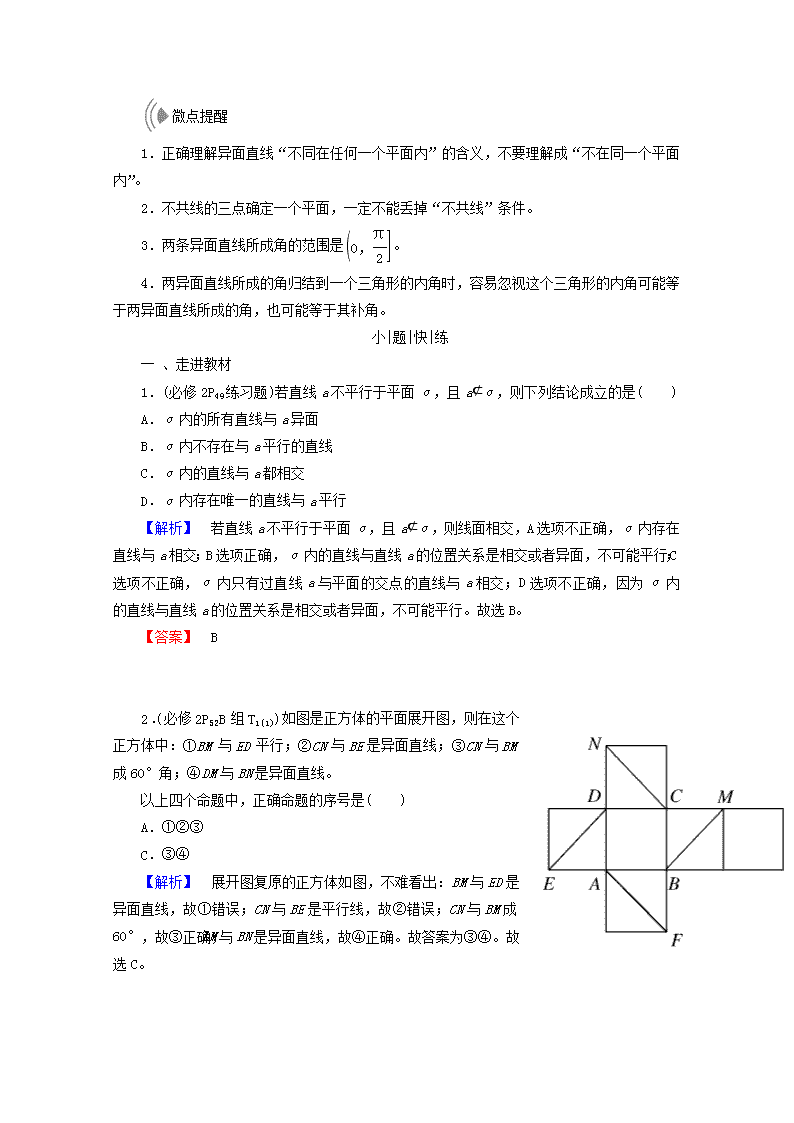‎ ‎3．直线与平面的位置关系 位置关系 图示 符号表示 公共点个数 直线l在平面α内 l⊂α 无数个 直线l与平面α相交 l∩α＝A 一个 直线l与平面α平行 l∥α ‎0个 微点提醒 ‎1．正确理解异面直线“不同在任何一个平面内”的含义，不要理解成“不在同一个平面内”。‎ ‎2．不共线的三点确定一个平面，一定不能丢掉“不共线”条件。‎ ‎3．两条异面直线所成角的范围是。‎ ‎4．两异面直线所成的角归结到一个三角形的内角时，容易忽视这个三角形的内角可能等于两异面直线所成的角，也可能等于其补角。‎ 小|题|快|练 一 、走进教材 ‎1．(必修2P49练习题)若直线a不平行于平面α，且a⊄α，则下列结论成立的是(　　)‎ A．α内的所有直线与a异面 B．α内不存在与a平行的直线 C．α内的直线与a都相交 D．α内存在唯一的直线与a平行 ‎【解析】　若直线a不平行于平面α，且a⊄α，则线面相交，A选项不正确，α内存在直线与a相交；B选项正确，α内的直线与直线a的位置关系是相交或者异面，不可能平行；C选项不正确，α内只有过直线a与平面的交点的直线与a相交；D选项不正确，因为α内的直线与直线a的位置关系是相交或者异面，不可能平行。故选B。‎ ‎【答案】　B ‎2．(必修2P52B组T1(1))如图是正方体的平面展开图，则在这个正方体中：①BM与ED平行；②CN与BE是异面直线；③CN与BM成60°角；④DM与BN是异面直线。‎ 以上四个命题中，正确命题的序号是(　　)‎ A．①②③ B．②④‎ C．③④ D．②③④‎ ‎【解析】　展开图复原的正方体如图，不难看出：BM与ED是异面直线，故①错误；CN与BE是平行线，故②错误；CN与BM成60°，故③正确；DM与BN是异面直线，故④正确。故答案为③④。故选C。‎ ‎【答案】　C 二、双基查验 ‎1．若空间三条直线a，b，c满足a⊥b，b∥c，则直线a与c(　　)‎ A．一定平行　　　　　　 B．一定相交 C．一定是异面直线 D．一定垂直 ‎【解析】　因为b∥c，a⊥b，所以a⊥c，即a与c垂直。故选D。‎ ‎【答案】　D ‎2．下列命题正确的个数为(　　)‎ ‎①经过三点确定一个平面 ‎②梯形可以确定一个平面 ‎③两两相交的三条直线最多可以确定三个平面 A．0个 B．1个 C．2个 D．3个 ‎【解析】　①错误，②③正确。故选C。‎ ‎【答案】　C ‎3.如图所示，已知在长方体ABCD－EFGH中，AB＝2，AD＝2，AE＝2，则BC和EG所成角的大小是________，AE和BG所成角的大小是________。‎ ‎【解析】　∵BC与EG所成的角等于EG与FG所成的角即∠EGF，tan∠EGF＝＝＝1，∴∠EGF＝45°，∵AE与BG所成的角等于BF与BG所成的角即∠GBF，tan∠GBF＝＝＝，∴∠GBF＝60°。‎ ‎【答案】　45°　60°‎ ‎4．已知空间四边形ABCD中，M，N分别为AB，CD的中点，则下列判断：①MN≥(AC＋‎ BD)；②MN>(AC＋BD)；③MN＝(AC＋BD)；④MN<(AC＋BD)。其中正确的是________。‎ ‎【解析】　如图，取BC的中点O，连接MO，NO，‎ 则OM＝AC，ON＝BD，‎ 在△MON中，MN