2014年山东省高考数学试卷（文科） 21页

‎2014年山东省高考数学试卷（文科） ‎ ‎　‎ 一.选择题每小题5分，共50分 ‎1．（5分）已知a，b∈R，i是虚数单位，若a+i=2﹣bi，则（a+bi）2=（　　）‎ A．3﹣4i B．3+4i C．4﹣3i D．4+3i ‎2．（5分）设集合A={x|x2﹣2x＜0}，B={x|1≤x≤4}，则A∩B=（　　）‎ A．（0，2] B．（1，2） C．[1，2） D．（1，4）‎ ‎3．（5分）函数f（x）=的定义域为（　　）‎ A．（0，2） B．（0，2] C．（2，+∞） D．[2，+∞）‎ ‎4．（5分）用反证法证明命题“设a，b为实数，则方程x3+ax+b=0至少有一个实根”时，要做的假设是（　　）‎ A．方程x3+ax+b=0没有实根 B．方程x3+ax+b=0至多有一个实根 C．方程x3+ax+b=0至多有两个实根 D．方程x3+ax+b=0恰好有两个实根 ‎5．（5分）已知实数x，y满足ax＜ay（0＜a＜1），则下列关系式恒成立的是（　　）‎ A．x3＞y3 B．sinx＞siny C．ln（x2+1）＞ln（y2+1） D．＞‎ ‎6．（5分）已知函数y=loga（x+c）（a，c为常数，其中a＞0，a≠1）的图象如图所示，则下列结论成立的是（　　）‎ A．a＞1，c＞1 B．a＞1，0＜c＜1 C．0＜a＜1，c＞1 D．0＜a＜1，0＜c＜1‎ ‎7．（5分）已知向量=（1，），=（3，m），若向量，的夹角为，则实数m=（　　）‎ A．2 B． C．0 D．﹣‎ ‎8．（5分）为了研究某药品的疗效，选取若干名志愿者进行临床试验．所有志愿者的舒张压数据（单位：kPa）的分组区间为[12，13），[13，14），[14，15），[15，16），[16，17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组．如图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为（　　）‎ A．6 B．8 C．12 D．18‎ ‎9．（5分）对于函数f（x），若存在常数a≠0，使得x取定义域内的每一个值，都有f（x）=f（2a﹣x），则称f（x）为准偶函数，下列函数中是准偶函数的是（　　）‎ A．f（x）= B．f（x）=x2 C．f（x）=tanx D．f（x）=cos（x+1）‎ ‎10．（5分）已知x，y满足约束条件，当目标函数z=ax+by（a＞0，b＞0）在该约束条件下取到最小值2时，a2+b2的最小值为（　　）‎ A．5 B．4 C． D．2‎ ‎　‎ 二.填空题每小题5分，共25分 ‎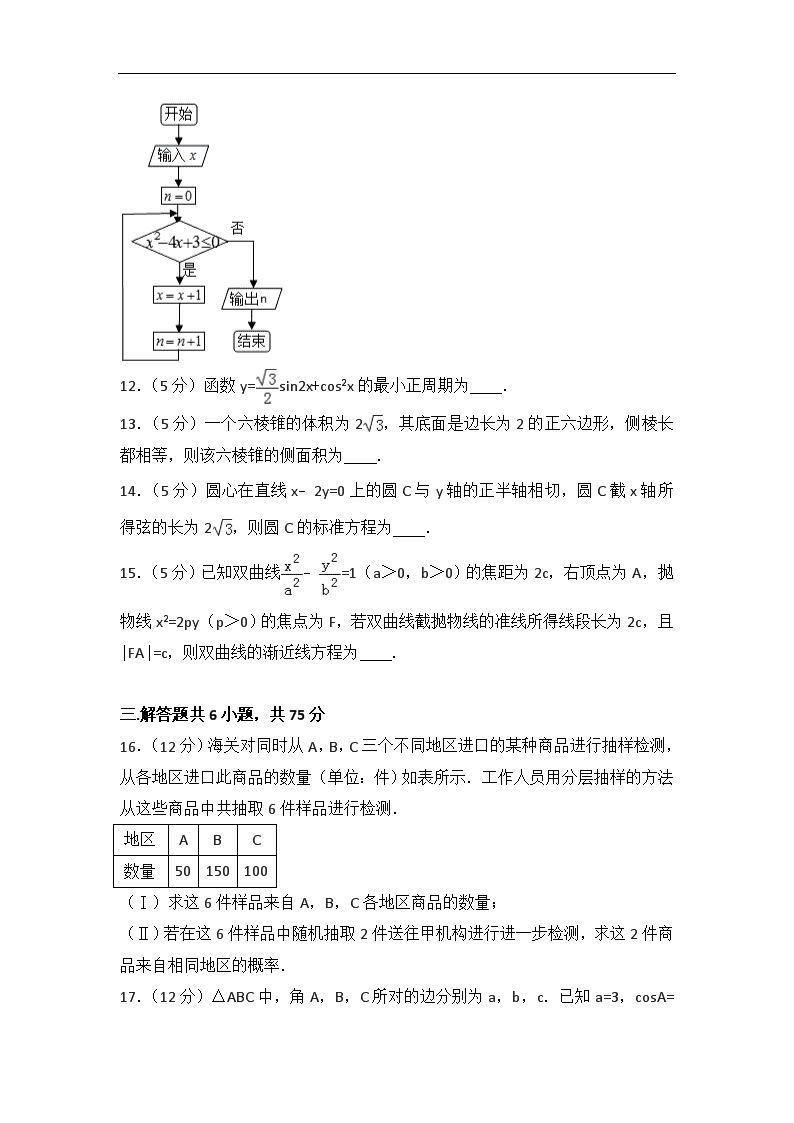11．（5分）执行如图所示的程序框图，若输入的x的值为1，则输出的n的值为　　．‎ ‎12．（5分）函数y=sin2x+cos2x的最小正周期为　　．‎ ‎13．（5分）一个六棱锥的体积为2，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为　　．‎ ‎14．（5分）圆心在直线x﹣2y=0上的圆C与y轴的正半轴相切，圆C截x轴所得弦的长为2，则圆C的标准方程为　　．‎ ‎15．（5分）已知双曲线﹣=1（a＞0，b＞0）的焦距为2c，右顶点为A，抛物线x2=2py（p＞0）的焦点为F，若双曲线截抛物线的准线所得线段长为2c，且|FA|=c，则双曲线的渐近线方程为　　．‎ ‎　‎ 三.解答题共6小题，共75分 ‎16．（12分）海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此商品的数量（单位：件）如表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．‎ 地区 A B C 数量 ‎50‎ ‎150‎ ‎100‎ ‎（Ⅰ）求这6件样品来自A，B，C各地区商品的数量；‎ ‎（Ⅱ）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．‎ ‎17．（12分）△ABC中，角A，B，C所对的边分别为a，b，c．已知a=3，cosA=‎ ‎，B=A+．‎ ‎（Ⅰ）求b的值；‎ ‎（Ⅱ）求△ABC的面积．‎ ‎18．（12分）如图，四棱锥P﹣ABCD中，AP⊥平面PCD，AD∥BC，AB=BC=AD，E，F分别为线段AD，PC的中点．‎ ‎（Ⅰ）求证：AP∥平面BEF；‎ ‎（Ⅱ）求证：BE⊥平面PAC．‎ ‎19．（12分）在等差数列{an}中，已知公差d=2，a2是a1与a4的等比中项．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）设bn=a，记Tn=﹣b1+b2﹣b3+b4﹣…+（﹣1）nbn，求Tn．‎ ‎20．（13分）设函数f（x）=alnx+，其中a为常数．‎ ‎（Ⅰ）若a=0，求曲线y=f（x）在点（1，f（1））处的切线方程；‎ ‎（Ⅱ）讨论函数f（x）的单调性．‎ ‎21．（14分）在平面直角坐标系xOy中，椭圆C：+=1（a＞b＞0）的离心率为，直线y=x被椭圆C截得的线段长为．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）过原点的直线与椭圆C交于A，B两点（A，B不是椭圆C的顶点）．点D在椭圆C上，且AD⊥AB，直线BD与x轴、y轴分别交于M，N两点．‎ ‎（i）设直线BD，AM的斜率分别为k1，k2，证明存在常数λ使得k1=λk2，并求出λ的值；‎ ‎（ii）求△OMN面积的最大值．‎ ‎　‎ ‎2014年山东省高考数学试卷（文科） ‎ 参考答案与试题解析 ‎　‎ 一.选择题每小题5分，共50分 ‎1．（5分）（2014•山东）已知a，b∈R，i是虚数单位，若a+i=2﹣bi，则（a+bi）2=（　　）‎ A．3﹣4i B．3+4i C．4﹣3i D．4+3i ‎【分析】利用两个复数相等的充要条件求得a、b的值，再利用两个复数代数形式的乘法法则求得（a+bi）2的值．‎ ‎【解答】解：∵a+i=2﹣bi，∴a=2、b=﹣1，则（a+bi）2=（2﹣i）2=3﹣4i，‎ 故选：A．‎ ‎　‎ ‎2．（5分）（2014•山东）设集合A={x|x2﹣2x＜0}，B={x|1≤x≤4}，则A∩B=（　　）‎ A．（0，2] B．（1，2） C．[1，2） D．（1，4）‎ ‎【分析】分别解出集合A和B，再根据交集的定义计算即可．‎ ‎【解答】解：A={x|0＜x＜2}，B={x|1≤x≤4}，‎ ‎∴A∩B={x|1≤x＜2}．‎ 故选：C．‎ ‎　‎ ‎3．（5分）（2014•山东）函数f（x）=的定义域为（　　）‎ A．（0，2） B．（0，2] C．（2，+∞） D．[2，+∞）‎ ‎【分析】分析可知，，解出x即可．‎ ‎【解答】解：由题意可得，，‎ 解得，即x＞2．‎ ‎∴所求定义域为（2，+∞）．‎ 故选：C．‎ ‎　‎ ‎4．（5分）（2014•山东）用反证法证明命题“设a，b为实数，则方程x3+ax+b=0至少有一个实根”时，要做的假设是（　　）‎ A．方程x3+ax+b=0没有实根 B．方程x3+ax+b=0至多有一个实根 C．方程x3+ax+b=0至多有两个实根 D．方程x3+ax+b=0恰好有两个实根 ‎【分析】直接利用命题的否定写出假设即可．‎ ‎【解答】解：反证法证明问题时，反设实际是命题的否定，‎ ‎∴用反证法证明命题“设a，b为实数，则方程x3+ax+b=0至少有一个实根”时，要做的假设是：方程x3+ax+b=0没有实根．‎ 故选：A．‎ ‎　‎ ‎5．（5分）（2014•山东）已知实数x，y满足ax＜ay（0＜a＜1），则下列关系式恒成立的是（　　）‎ A．x3＞y3 B．sinx＞siny C．ln（x2+1）＞ln（y2+1） D．＞‎ ‎【分析】本题主要考查不等式的大小比较，利用函数的单调性的性质是解决本题的关键．‎ ‎【解答】解：∵实数x，y满足ax＜ay（0＜a＜1），∴x＞y，‎ A．当x＞y时，x3＞y3，恒成立，‎ B．当x=π，y=时，满足x＞y，但sinx＞siny不成立．‎ C．若ln（x2+1）＞ln（y2+1），则等价为x2＞y2成立，当x=1，y=﹣1时，满足x＞y，但x2＞y2不成立．‎ D．若＞，则等价为x2+1＜y2+1，即x2＜y2，当x=1，y=﹣1时，满足x＞y，但x2＜y2不成立．‎ 故选：A．‎ ‎　‎ ‎6．（5分）（2014•山东）已知函数y=loga（x+c）（a，c为常数，其中a＞0，a≠1）的图象如图所示，则下列结论成立的是（　　）‎ A．a＞1，c＞1 B．a＞1，0＜c＜1 C．0＜a＜1，c＞1 D．0＜a＜1，0＜c＜1‎ ‎【分析】根据对数函数的图象和性质即可得到结论．‎ ‎【解答】解：∵函数单调递减，∴0＜a＜1，‎ 当x=1时loga（x+c）=loga（1+c）＜0，即1+c＞1，即c＞0，‎ 当x=0时loga（x+c）=logac＞0，即c＜1，即0＜c＜1，‎ 故选：D．‎ ‎　‎ ‎7．（5分）（2014•山东）已知向量=（1，），=（3，m），若向量，的夹角为，则实数m=（　　）‎ A．2 B． C．0 D．﹣‎ ‎【分析】由条件利用两个向量的夹角公式、两个向量的数量积公式，求得m的值．‎ ‎【解答】解：由题意可得cos===，‎ 解得 m=，‎ 故选：B．‎ ‎　‎ ‎8．（5分）（2014•山东）为了研究某药品的疗效，选取若干名志愿者进行临床试验．所有志愿者的舒张压数据（单位：kPa）的分组区间为[12，13），[13，14），[14，15），[15，16），[16，17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组．如图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为（　　）‎ A．6 B．8 C．12 D．18‎ ‎【分析】由频率=以及直方图可得分布在区间第一组与第二组共有20人的频率，即可求出第三组中有疗效的人数得到答案；‎ ‎【解答】解：由直方图可得分布在区间第一组与第二组共有20人，分布在区间第一组与第二组的频率分别为0.24，0.16，所以第一组有12人，第二组8人，第三组的频率为0.36，所以第三组的人数：18人，‎ 第三组中没有疗效的有6人，‎ 第三组中有疗效的有12人．‎ 故选：C．‎ ‎　‎ ‎9．（5分）（2014•山东）对于函数f（x），若存在常数a≠0，使得x取定义域内的每一个值，都有f（x）=f（2a﹣x），则称f（x）为准偶函数，下列函数中是准偶函数的是（　　）‎ A．f（x）= B．f（x）=x2 C．f（x）=tanx D．f（x）=cos（x+1）‎ ‎【分析】由题意判断f（x）为准偶函数的对称轴，然后判断选项即可．‎ ‎【解答】解：对于函数f（x），若存在常数a≠0，使得x取定义域内的每一个值，都有f（x）=f（2a﹣x），则称f（x）为准偶函数，‎ ‎∴函数的对称轴是x=a，a≠0，‎ 选项A函数没有对称轴；选项B、函数的对称轴是x=0，选项C，函数没有对称轴．‎ 函数f（x）=cos（x+1），有对称轴，且x=0不是对称轴，选项D正确．‎ 故选：D．‎ ‎　‎ ‎10．（5分）（2014•山东）已知x，y满足约束条件，当目标函数z=ax+by（a＞0，b＞0）在该约束条件下取到最小值2时，a2+b2的最小值为（　　）‎ A．5 B．4 C． D．2‎ ‎【分析】由约束条件正常可行域，然后求出使目标函数取得最小值的点的坐标，代入目标函数得到2a+b﹣2=0．a2+b2的几何意义为坐标原点到直线2a+b﹣2=0的距离的平方，然后由点到直线的距离公式得答案．‎ ‎【解答】解：由约束条件作可行域如图，‎ 联立，解得：A（2，1）．‎ 化目标函数为直线方程得：（b＞0）．‎ 由图可知，当直线过A点时，直线在y轴上的截距最小，z最小．‎ ‎∴2a+b=2．‎ 即2a+b﹣2=0．‎ 则a2+b2的最小值为．‎ 故选：B．‎ ‎　‎ 二.填空题每小题5分，共25分 ‎11．（5分）（2014•山东）执行如图所示的程序框图，若输入的x的值为1，则输出的n的值为　3　．‎ ‎【分析】计算循环中不等式的值，当不等式的值大于0时，不满足判断框的条件，退出循环，输出结果即可．‎ ‎【解答】解：循环前输入的x的值为1，‎ 第1次循环，x2﹣4x+3=0≤0，‎ 满足判断框条件，x=2，n=1，x2﹣4x+3=﹣1≤0，‎ 满足判断框条件，x=3，n=2，x2﹣4x+3=0≤0‎ 满足判断框条件，x=4，n=3，x2﹣4x+3=3＞0，不满足判断框条件，‎ 输出n：3．‎ 故答案为：3．‎ ‎　‎ ‎12．（5分）（2014•山东）函数y=sin2x+cos2x的最小正周期为　π　．‎ ‎【分析】利用两角和的正弦公式、二倍角的余弦公式化简函数的解析式为f（x）=sin（2x+），从而求得函数的最小正周期 ‎【解答】解：∵函数y=sin2x+cos2x=sin2x+=sin（2x+）+，‎ 故函数的最小正周期的最小正周期为 =π，‎ 故答案为：π．‎ ‎　‎ ‎13．（5分）（2014•山东）一个六棱锥的体积为2，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为　12　．‎ ‎【分析】判断棱锥是正六棱锥，利用体积求出棱锥的高，然后求出斜高，即可求解侧面积．‎ ‎【解答】解：∵一个六棱锥的体积为2，其底面是边长为2的正六边形，侧棱长都相等，∴棱锥是正六棱锥，设棱锥的高为h，则，‎ ‎∴h=1，‎ 棱锥的斜高为：==2，‎ 该六棱锥的侧面积为：=12．‎ 故答案为：12．‎ ‎　‎ ‎14．（5分）（2014•山东）圆心在直线x﹣2y=0上的圆C与y轴的正半轴相切，圆C截x轴所得弦的长为2，则圆C的标准方程为　（x﹣2）2+（y﹣1）2=4　．‎ ‎【分析】‎ 由圆心在直线x﹣2y=0上，设出圆心坐标，再根据圆与y轴相切，得到圆心到y轴的距离即圆心横坐标的绝对值等于圆的半径，表示出半径r，由弦长的一半，圆的半径r及表示出的d利用勾股定理列出关于t的方程，求出方程的解得到t的值，从而得到圆心坐标和半径，根据圆心和半径写出圆的方程即可．‎ ‎【解答】解：设圆心为（2t，t），半径为r=|2t|，‎ ‎∵圆C截x轴所得弦的长为2，‎ ‎∴t2+3=4t2，‎ ‎∴t=±1，‎ ‎∵圆C与y轴的正半轴相切，‎ ‎∴t=﹣1不符合题意，舍去，‎ 故t=1，2t=2，‎ ‎∴（x﹣2）2+（y﹣1）2=4．‎ 故答案为：（x﹣2）2+（y﹣1）2=4．‎ ‎　‎ ‎15．（5分）（2014•山东）已知双曲线﹣=1（a＞0，b＞0）的焦距为2c，右顶点为A，抛物线x2=2py（p＞0）的焦点为F，若双曲线截抛物线的准线所得线段长为2c，且|FA|=c，则双曲线的渐近线方程为　y=±x　．‎ ‎【分析】求出双曲线的右顶点A（a，0），拋物线x2=2py（p＞0）的焦点及准线方程，根据已知条件得出及，求出a=b，得双曲线的渐近线方程为：y=±x．‎ ‎【解答】解：∵右顶点为A，‎ ‎∴A（a，0），‎ ‎∵F为抛物线x2=2py（p＞0）的焦点，‎ F，‎ ‎∵|FA|=c，‎ ‎∴‎ 抛物线的准线方程为 由得，‎ ‎，‎ 由①②，得=2c，即c2=2a2，‎ ‎∵c2=a2+b2，‎ ‎∴a=b，‎ ‎∴双曲线的渐近线方程为：y=±x，‎ 故答案为：y=±x．‎ ‎　‎ 三.解答题共6小题，共75分 ‎16．（12分）（2014•山东）海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此商品的数量（单位：件）如表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．‎ 地区 A B C 数量 ‎50‎ ‎150‎ ‎100‎ ‎（Ⅰ）求这6件样品来自A，B，C各地区商品的数量；‎ ‎（Ⅱ）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．‎ ‎【分析】（Ⅰ）先计算出抽样比，进而可求出这6件样品来自A，B，C各地区商品的数量；‎ ‎（Ⅱ）先计算在这6件样品中随机抽取2件的基本事件总数，及这2件商品来自相同地区的事件个数，代入古典概型概率计算公式，可得答案．‎ ‎【解答】解：（Ⅰ）A，B，C三个地区商品的总数量为50+150+100=300，‎ 故抽样比k==，‎ 故A地区抽取的商品的数量为：×50=1；‎ B地区抽取的商品的数量为：×150=3；‎ C地区抽取的商品的数量为：×100=2；‎ ‎（Ⅱ）在这6件样品中随机抽取2件共有：=15个不同的基本事件；‎ 且这些事件是等可能发生的，‎ 记“这2件商品来自相同地区”为事件A，则这2件商品可能都来自B地区或C地区，‎ 则A中包含=4种不同的基本事件，‎ 故P（A）=，‎ 即这2件商品来自相同地区的概率为．‎ ‎　‎ ‎17．（12分）（2014•山东）△ABC中，角A，B，C所对的边分别为a，b，c．已知a=3，cosA=，B=A+．‎ ‎（Ⅰ）求b的值；‎ ‎（Ⅱ）求△ABC的面积．‎ ‎【分析】（Ⅰ）利用cosA求得sinA，进而利用A和B的关系求得sinB，最后利用正弦定理求得b的值．‎ ‎（Ⅱ）利用sinB，求得cosB的值，进而根两角和公式求得sinC的值，最后利用三角形面积公式求得答案．‎ ‎【解答】解：（Ⅰ）∵cosA=，‎ ‎∴sinA==，‎ ‎∵B=A+．‎ ‎∴sinB=sin（A+）=cosA=，‎ 由正弦定理知=，‎ ‎∴b=•sinB=×=3．‎ ‎（Ⅱ）∵sinB=，B=A+＞‎ ‎∴cosB=﹣=﹣，‎ sinC=sin（π﹣A﹣B）=sin（A+B）=sinAcosB+cosAsinB=×（﹣）+×=，‎ ‎∴S=a•b•sinC=×3×3×=．‎ ‎　‎ ‎18．（12分）（2014•山东）如图，四棱锥P﹣ABCD中，AP⊥平面PCD，AD∥BC，AB=BC=AD，E，F分别为线段AD，PC的中点．‎ ‎（Ⅰ）求证：AP∥平面BEF；‎ ‎（Ⅱ）求证：BE⊥平面PAC．‎ ‎【分析】（Ⅰ）证明四边形ABCE是平行四边形，可得O是AC的中点，利用F为线段PC的中点，可得PA∥OF，从而可证AP∥平面BEF；‎ ‎（Ⅱ）证明BE⊥AP、BE⊥AC，即可证明BE⊥平面PAC．‎ ‎【解答】证明：（Ⅰ）连接CE，则 ‎∵AD∥BC，BC=AD，E为线段AD的中点，‎ ‎∴四边形ABCE是平行四边形，BCDE是平行四边形，‎ 设AC∩BE=O，连接OF，则O是AC的中点，‎ ‎∵F为线段PC的中点，‎ ‎∴PA∥OF，‎ ‎∵PA⊄平面BEF，OF⊂平面BEF，‎ ‎∴AP∥平面BEF；‎ ‎（Ⅱ）∵BCDE是平行四边形，‎ ‎∴BE∥CD，‎ ‎∵AP⊥平面PCD，CD⊂平面PCD，‎ ‎∴AP⊥CD，‎ ‎∴BE⊥AP，‎ ‎∵AB=BC，四边形ABCE是平行四边形，‎ ‎∴四边形ABCE是菱形，‎ ‎∴BE⊥AC，‎ ‎∵AP∩AC=A，‎ ‎∴BE⊥平面PAC．‎ ‎　‎ ‎19．（12分）（2014•山东）在等差数列{an}中，已知公差d=2，a2是a1与a4的等比中项．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）设bn=a，记Tn=﹣b1+b2﹣b3+b4﹣…+（﹣1）nbn，求Tn．‎ ‎【分析】（Ⅰ）由于a2是a1与a4的等比中项，可得，再利用等差数列的通项公式即可得出．‎ ‎（Ⅱ）利用（Ⅰ）可得bn=a=n（n+1），因此Tn=﹣b1+b2﹣b3+b4﹣…+（﹣1）nbn=﹣1×（1+1）+2×（2+1）﹣…+（﹣1）nn•（n+1）．对n分奇偶讨论即可得出．‎ ‎【解答】解：（Ⅰ）∵a2是a1与a4的等比中项，‎ ‎∴，‎ ‎∵在等差数列{an}中，公差d=2，‎ ‎∴，即，‎ 化为，解得a1=2．‎ ‎∴an=a1+（n﹣1）d=2+（n﹣1）×2=2n．‎ ‎（Ⅱ）∵bn=a=n（n+1），‎ ‎∴Tn=﹣b1+b2﹣b3+b4﹣…+（﹣1）nbn=﹣1×（1+1）+2×（2+1）﹣…+（﹣1）nn•（n+1）．‎ 当n=2k（k∈N*）时，b2k﹣b2k﹣1=2k（2k+1）﹣（2k﹣1）（2k﹣1+1）=4k Tn=（b2﹣b1）+（b4﹣b3）+…+（b2k﹣b2k﹣1）‎ ‎=4（1+2+…+k）=4×=2k（k+1）=．‎ 当n=2k﹣1（k∈N*）时，‎ Tn=（b2﹣b1）+（b4﹣b3）+…+（b2k﹣2﹣b2k﹣3）﹣b2k﹣1‎ ‎=n（n+1）‎ ‎=﹣．‎ 故Tn=．‎ ‎　‎ ‎20．（13分）（2014•山东）设函数f（x）=alnx+，其中a为常数．‎ ‎（Ⅰ）若a=0，求曲线y=f（x）在点（1，f（1））处的切线方程；‎ ‎（Ⅱ）讨论函数f（x）的单调性．‎ ‎【分析】（Ⅰ）根据导数的几何意义，曲线y=f（x）在x=1处的切线方程为y﹣f（1）=f′（1）（x﹣1），代入计算即可．‎ ‎（Ⅱ）先对其进行求导，即，考虑函数g（x）=ax2+（2a+2）x+a，分成a≥0，﹣＜a＜0，a≤﹣三种情况分别讨论即可．‎ ‎【解答】解：，‎ ‎（Ⅰ）当a=0时，，f′（1）=，f（1）=0‎ ‎∴曲线y=f（x）在点（1，f（1））处的切线方程为y=（x﹣1）．‎ ‎（Ⅱ）（1）当a≥0时，由x＞0知f′（x）＞0，即f（x）在（0，+∞）上单调递增；‎ ‎（2）当a＜0时，令f′（x）＞0，则＞0，整理得，ax2+（2a+2）x+a＞0，‎ 令f′（x）＜0，则＜0，整理得，ax2+（2a+2）x+a＜0．‎ 以下考虑函数g（x）=ax2+（2a+2）x+a，g（0）=a＜0.，对称轴方程．‎ ‎①当a≤﹣时，△≤0，∴g（x）＜0恒成立．（x＞0）‎ ‎②当﹣＜a＜0时，此时，对称轴方程＞0，‎ ‎∴g（x）=0的两根一正一负，计算得 当0＜x＜时，g（x）＞0；‎ 当x＞时，g（x）＜0．‎ 综合（1）（2）可知，‎ 当a≤﹣时，f（x）在（0，+∞）上单调递减；‎ 当﹣＜a＜0时，f（x）在（0，）上单调递增，在（，+∞）上单调递减；‎ 当a＞0时，f（x）在（0，+∞）上单调递增．‎ ‎　‎ ‎21．（14分）（2014•山东）在平面直角坐标系xOy中，椭圆C：+=1（a＞b＞0）的离心率为，直线y=x被椭圆C截得的线段长为．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）过原点的直线与椭圆C交于A，B两点（A，B不是椭圆C的顶点）．点D在椭圆C上，且AD⊥AB，直线BD与x轴、y轴分别交于M，N两点．‎ ‎（i）设直线BD，AM的斜率分别为k1，k2，证明存在常数λ使得k1=λk2，并求出λ的值；‎ ‎（ii）求△OMN面积的最大值．‎ ‎【分析】（Ⅰ）由椭圆离心率得到a，b的关系，化简椭圆方程，和直线方程联立后求出交点的横坐标，把弦长用交点横坐标表示，则a的值可求，进一步得到b的值，则椭圆方程可求；‎ ‎（Ⅱ）（i）设出A，D的坐标分别为（x1，y1）（x1y1≠0），（x2，y2），用A的坐标表示B的坐标，把AB和AD的斜率都用A的坐标表示，写出直线AD的方程，和椭圆方程联立后利用根与系数关系得到AD横纵坐标的和，求出AD中点坐标，则BD斜率可求，再写出BD所在直线方程，取y=0得到M点坐标，由两点求斜率得到AM的斜率，由两直线斜率的关系得到λ的值；‎ ‎（ii）由BD方程求出N点坐标，结合（i）中求得的M的坐标得到△OMN的面积，然后结合椭圆方程利用基本不等式求最值．‎ ‎【解答】解：（Ⅰ）由题意知，，则a2=4b2．‎ ‎∴椭圆C的方程可化为x2+4y2=a2．‎ 将y=x代入可得，‎ 因此，解得a=2．‎ 则b=1．‎ ‎∴椭圆C的方程为；‎ ‎（Ⅱ）（i）设A（x1，y1）（x1y1≠0），D（x2，y2），‎ 则B（﹣x1，﹣y1）．‎ ‎∵直线AB的斜率，‎ 又AB⊥AD，‎ ‎∴直线AD的斜率．‎ 设AD方程为y=kx+m，‎ 由题意知k≠0，m≠0．‎ 联立，得（1+4k2）x2+8kmx+4m2﹣4=0．‎ ‎∴．‎ 因此．‎ 由题意可得．‎ ‎∴直线BD的方程为．‎ 令y=0，得x=3x1，即M（3x1，0）．‎ 可得．‎ ‎∴，即．‎ 因此存在常数使得结论成立．‎ ‎（ii）直线BD方程为，‎ 令x=0，得，即N（）．‎ 由（i）知M（3x1，0），‎ 可得△OMN的面积为S==．‎ 当且仅当时等号成立．‎ ‎∴△OMN面积的最大值为．‎ ‎　‎ 参与本试卷答题和审题的老师有：caoqz；任老师；qiss；maths；sxs123；刘长柏；wdnah；豫汝王世崇；wsj1012；沂蒙松（排名不分先后）‎ ‎2017年2月3日