2020高中数学 第2章 函数概念与基本初等函数I 2 7页

1 函数的单调性 （答题时间：30 分钟） 一、填空题 1. 函数 21  xy 的最小值是__________。 2. 设函数 )(xf      ,0,6 ,0,642 xx xxx 则不等式 )1()( fxf  的解集为________。 3. 已知函数 )(xf 1 3   a ax （ 1a ） （1）若 0a ，则 )(xf 的定义域是___________； （2）若 )(xf 在区间 ]1,0( 上是减函数，则实数 a 的取值范围是________。 4. 已知函数 3 2 , 2,( ) ( 1) , 2. xf x x x x       若关于 x 的方程 ( )f x k 有两个不同的实根，则实 数 k 的取值范围是 ____________。 5. 设 Ra ，若 0x 时均有 ]1)1[(  xa )1( 2  axx ≥0，则 a _________。 6. 若关于 x 的方程 2 2 kxx x  有四个不同的实数解，则实数 k 的取值范围是_______。 7. （1）二次函数 2( ) 4 5f x x mx   在[ 2, ]  上是增函数，则 (1)f 的取值范围是 _________； （2）已知函数 2( )f x x x  ，若 2( 1) (2)f m f   ，则实数 m 的取值范围是______。 8. 若不等式 22 1212 2  aaxx 对任意实数 x 恒成立，则实数 a 的取值范围是 ____________。 二、解答题 9. 设 )(xf 是定义在 R 上的函数，对 m 、 Rn  恒有 )()()( nfmfnmf  ，且当 0x 时， 1)(0  xf 。 （1）求证： 1)0( f ； （2）证明： Rx  时恒有 0)( xf ； （3）求证： )(xf 在 R 上是减函数； （4）若 ( ) (2 ) 1f x f x   ，求 x 的取值范围。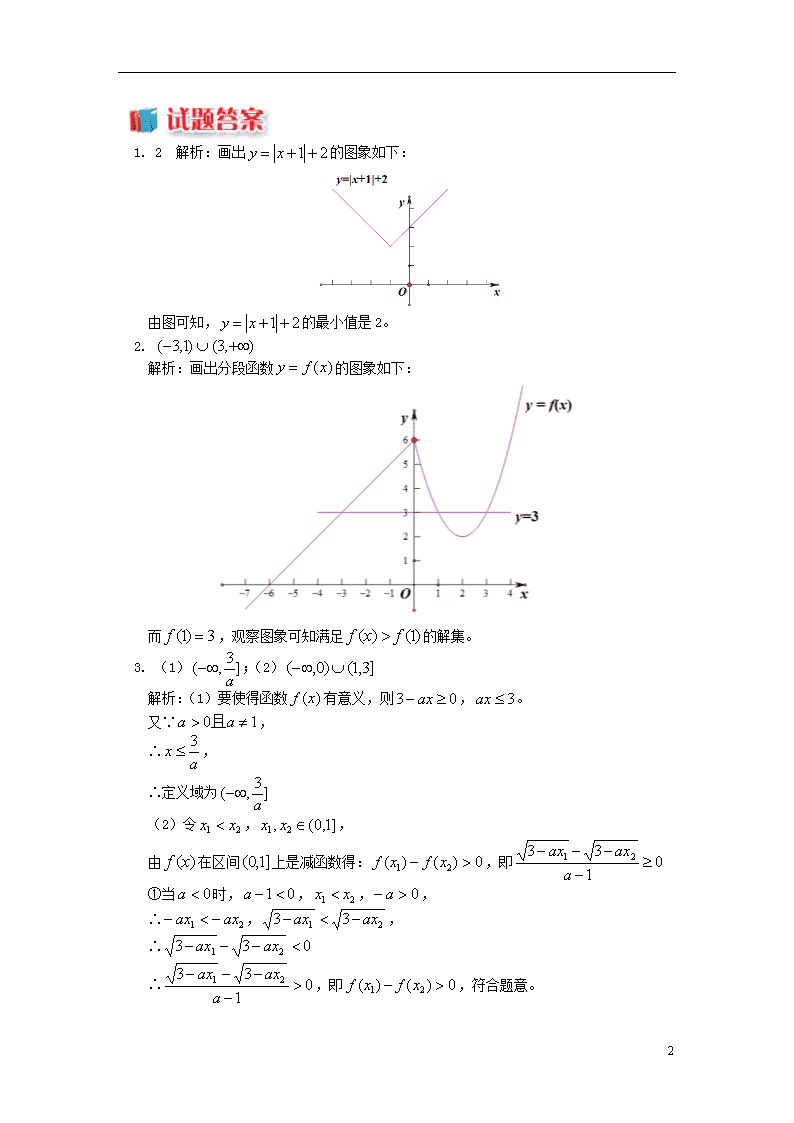 2 1. 2 解析：画出 21  xy 的图象如下： 由图可知， 21  xy 的最小值是 2。 2. ),3()1,3(  解析：画出分段函数 )(xfy  的图象如下： 而 3)1( f ，观察图象可知满足 )1()( fxf  的解集。 3. （1） ]3,( a  ；（2） ]3,1()0,(  解析：（1）要使得函数 )(xf 有意义，则 03  ax ， 3ax 。 又∵ 10  aa 且 ， ∴ ax 3 ， ∴定义域为 ]3,( a  （2）令 21 xx  ， ]1,0(, 21 xx ， 由 )(xf 在区间 ]1,0( 上是减函数得： 0)()( 21  xfxf ，即 01 33 21   a axax ①当 0a 时， 01a ， 21 xx  ， 0 a ， ∴ 1ax  2ax ， 21 33 axax  ， ∴ 21 33 axax  0 ∴ 01 33 21   a axax ，即 0)()( 21  xfxf ，符合题意。 3 ②当 0a 时 )(xf 3 为常数，不符合题意。 ③当 10  a 时， 01a ， 21 xx  ， 0a ∴ 1ax 2ax ， 21 33 axax  ， ∴ 21 33 axax  0 ， ∴ 01 33 21   a axax ，即 0)()( 21  xfxf ，不符合题意。 ④当 31  a 时， 01a ， 21 xx  ， 0a ∴ 1ax  2ax ， 21 33 axax  ， ∴ 21 33 axax  0 ， ∴ 01 33 21   a axax ，即 0)()( 21  xfxf ，符合题意。 ⑤当 3a 时， ]1,0(x ，不一定所有的 ax3 有意义，不符合题意。 综上所述，实数 a 的取值范围为 ]3,1()0,(  。 4. （0，1） 解析：画出分段函数 3 2 , 2,( ) ( 1) , 2. xf x x x x       的图象如下： ( )f x k 是一条平行于 x 轴的直线。 要使得关于 x 的方程 ( )f x k 有两个不同的实根， 就要使得 ( )f x k 与 3 2 , 2,( ) ( 1) , 2. xf x x x x       的函数图象有两个交点。 由图可知， 10  k 。 5. 2 3 解析：令 1)1()(  xaxf ， 1)( 2  axxxg 要使得 ]1)1[(  xa )1( 2  axx ≥0， 则 )(xf 与 )(xg 在同一点处的函数值同号，或同时为 0。 且 )(xf 与 )(xg 的零点相同 4 又 x 时， 1)( 2  axxxg 0 ， ∴ x 时， 1)1()(  xaxf 0 ， ∴ 1,01  aa 画出符合题意的函数图象如下： 令 )(xf 0 ，∴ x 1 1 a ∴ )1 1( ag 0 ， 即 )1(011)1 1( 2  aa a a 两边同时乘以 )1( a ，化简整理得： 032 2  aa ，又 1a ， ∴ 2 3a 。 6. （ ,1 ） 解析：观察方程 2 2 kxx x  可知有一个解为 0x ， 所以关于 x 的方程 2 2 kxx x  有四个不同的实数解等价于 2 2 kxx x  有三个不同的非零实数解。 由 2 2 kxx x  得 k 2)2( xx x           .0,)2( 1 ,0,)2( 1 xxx xxx ∴ k 1       .0),2( ,0),2( xxx xxx 令 kxf 1)(  ， )(xg      .0),2( ,0),2( xxx xxx 则 )(xf 与 )(xg 的图象有三个交点。 画出符合条件的 )(xf 与 )(xg 的图象如下图： 5 由图可知： 110  k ，∴ 1k 。 7. （1） ),25[  ；（2） )1,1( 解析：（1）画出符合题意的 )(xf 的图象如下图： 由图可知：二次函数 2( ) 4 5f x x mx   的对称轴直线方程为 28  mx ， ∴ 16m ， 16 m 。 又∵ mf  9)1( ， ∴ 25)1( f 。 （2） 2( )f x x x       .0, ,0, 2 2 xxx xxx 画出 )(xf 的图象如下图： ∵ )2(2)2(  ff ，又∵ 2( 1) (2)f m f   ， 6 ∴ 212 2  m ， 解得： 11  m 。 8. ]2 1,1[ 解析：令 )(xf 212  xx             .2,13 ,2 12,3 ,2 1,13 xx xx xx 令 22 1)( 2  aaag ， 分别画出 )(xf ， )(ag 的函数图象如下： 要使得 )()( agxf  对任意实数 x 恒成立， 只须使 )(ag 小于或等于 )(xf 的最小值即可。 由图可知， 2 5)2 1()( min  fxf ， ∴ 2 522 1)( 2  aaag ， 解得： 2 11  a 。 9. （1）证明：令 0,1  nm ，代入到 )()()( nfmfnmf  中， 则： )0()1()1( fff  ， 又∵当 0x 时， 1)(0  xf ，∴ 1)1(0  f ∴ 1)1( )1()0(  f ff 。 （2）证明：当 0x 时， 0 x ，∴ 1)(0  xf 则 )]([ xxf  = )()( xfxf  = 1)0( f ， 又 1)(0  xf ，∴ 1)( xf 故当 0x 时， 01)( xf ； 当 0x 时， 1)(0  xf ； 当 0x 时， 01)0( f 综上所述， Rx  时恒有 0)( xf 。 （3）证明：任意取 Rxx 21, ，且 21 xx  ； 7  )()( 21 xfxf )()( 2221 xfxxxf  )()()( 2221 xfxfxxf  ]1)([)( 212  xxfxf ， 又∵ 21 xx  ，∴ 021  xx ； 又当 0x 时， 01)( xf ， ∴ 1)( 21  xxf ，∴ 01)( 21  xxf ， 又∵ 0)( 2 xf ， ∴ 0)()( 21  xfxf ∴ )(xf 在 R 上是减函数。 （4）解：∵ 1)2()(  xfxf ， 又∵ 1)0( f ， )(xf 在 R 上为减函数， )2()( xfxf  )2( xxf  )2(f 1)0(  f ∴ 1)2()(  xfxf 无解。