2020年西南名校高考数学模拟试卷(理科)(3月份) (含答案解析) 19页

2020 年西南名校高考数学模拟试卷(理科)(3 月份) 一、单项选择题（本大题共 12小题，共 60.0分） 1. 设全集 全 集，集合 全 ሼ1 ሼ ͳ，集合 全 ሼݔ ሼ 䁪，则 ㌳ 全 ㌳ A. ሼ1 ሼ ݔ B. ሼሼ ݔ C. ሼሼ 䁪 D. ሼ1 ሼ ݔ .ݔ 若复数 全 1 ͳ㌳ͳ ㌳在复平面内对应的点在第一象限，其中ݔ ͳ 集，i为虚数单位，则实 数 a取值范围是㌳ A. 香䁥 ㌳ݔ B. 䁥ݔ ㌳ C. 䁥 ㌳ݔ D. 䁥香㌳ݔ 3. 已知命题 p：不等式 ሼݔ ሼݔ 香的解集是ሼሼ 香或 ሼ ㈠ 命题，ݔ q“在 中， ㈠ 是 ㈠ 的充要条件”则㌳ A. p真 q假 B. 假 C. 真 D. p假 q真 ͳ. 在等比数列ͳ中，首项ͳ1 全 ，公比 全 1 ݔ ，那么数列ͳ的前 5项和䁪的值是㌳ A. 31 ݔ B. 33 ݔ C. 3䁪 ݔ D. 3 ݔ 䁪. 若双曲线 ሼݔ ͳݔ ݔ ݔ 全 1ͳ ㈠ 香䁥 ㈠ 香㌳的一条渐近线与过其右焦点的直线 全 ሼݔ ݔ 䁪平行，则该双 曲线的实轴长为㌳ A. 1 B. 2 C. 3 D. 4 6. 某四面体的三视图如图所示，则该四面体的所有棱长中最长的是 ㌳ A. 䁪 ݔ B. 5 C. ͳ1 D. ͳ ݔ 7. 将函数 的图象向左平移 ͳ个单位得到 ሼ 的图象，则 ㌳ A. ሼ 全 sinݔሼ B. C. ሼ 全 sinݔሼ D. 8. 已知圆 C：ሼݔ ݔ ͳሼ 全 香，直线 l：ሼ 3 全 香，则㌳ A. l与 C相交 B. l与 C相切 C. l与 C相离 D. 以上三个选项均有可能 9. 若1 ሼ㌳䁪ݔ ͳ ሼ㌳䁪ݔ 全 ͳ1ሼ ͳݔሼݔ ͳ3ሼ3 ͳͳሼͳ ͳ䁪ሼ䁪，则 ͳ ͳ1 ͳ3 ͳ䁪 全 ㌳ A. 0 B. 1 C. 243 D. 2 10. 四面体 ABCD的外接球为 O， 平面 ABC， 全 ，ݔ 全 3香， 全 3，则球 O的表 面积为㌳ A. ݔ3 B. 16 C. ݔ1 D. ݔݔ 3 11. 己知函数 ሼ㌳ 全 lgሼ 1㌳ ͳሼ香 ͳ 1㌳有两个零点ሼ1，ሼݔ，则有㌳ A. ሼ1ሼݔ 1 B. ሼ1ሼݔ ሼ1 ሼݔ C. ሼ1ሼݔ 全 ሼ1 ሼݔ D. ሼ1ሼݔ ㈠ ሼ1 ሼݔ 12. 函数 ሼ㌳ 全 1 ݔ1 ሼͳ 1 ݔ ͳሼݔ，若 ሼ㌳的导函数 ̵ሼ㌳在 R上是增函数，则实数 a的取值范围是㌳ A. ͳ 香 B. ͳ 香 C. ͳ 香 D. ͳ ㈠ 香 二、填空题（本大题共 4小题，共 20.0分） 13. 已知ͳ 全 1䁥ݔሼ㌳， 全 䁥ݔ 1㌳，且ͳ ，则 ሼ 全 ______ ． 14. 设 x、y满足约束条件 ሼ 1 香 3ሼ 1 香 ሼ ͳ ，若 全 ሼ 的最大值为 5a，则 ͳ 全________． 15. 在 中， 全 3 全 6，tan 全 3，点 D，E分别是边 AB，AC上的点，且 ‸ 全 3， 记 ‸，四边形 BCED的面积分别为1，ݔ，则 1 ݔ 的最大值为______ 16. 设抛物线 C：ݔ 全 ሼ的焦点为 F，直线 l过 F且与抛物线交于 P，Q两点．若 全 ݔ3 3 ，且 ㈠ ，则 全______． 三、解答题（本大题共 7小题，共 82.0分） 17. 已知数列ͳ中，ͳ1 全 且ͳݔ 全 ͳ1ݔ ݔ 䁥ݔ ㌳. 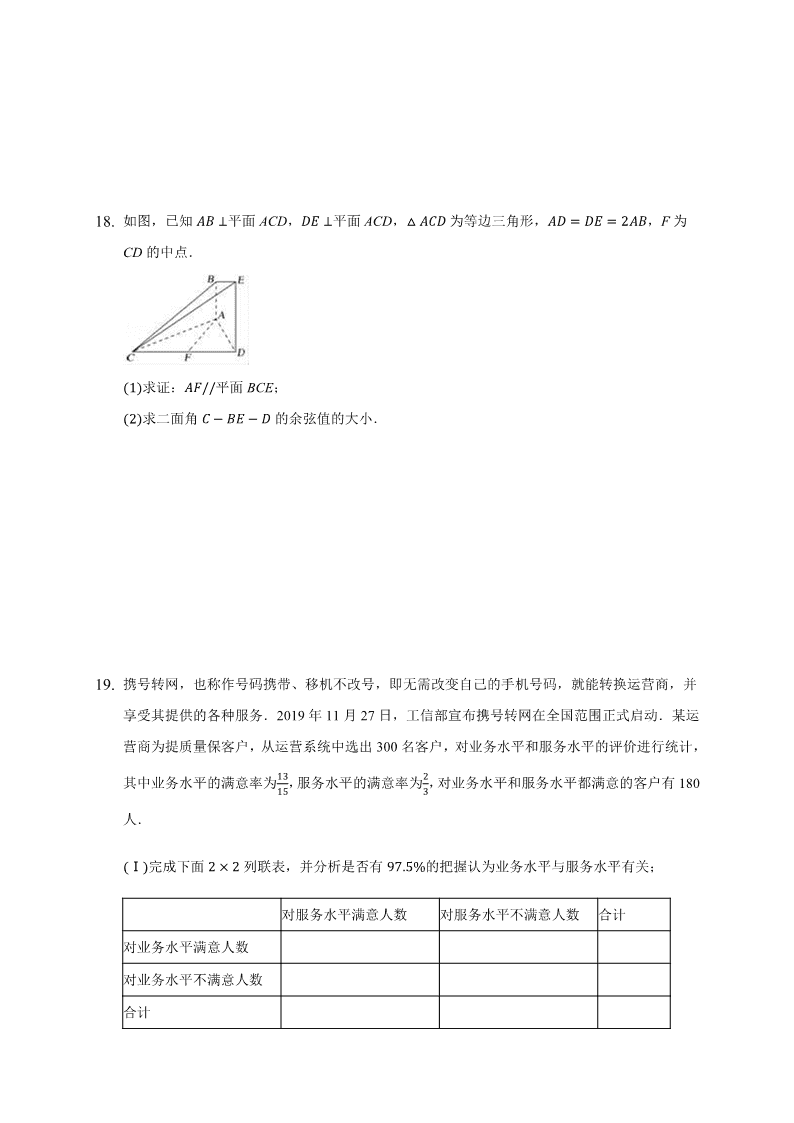1㌳证明ͳ 是等比数列； ㌳设ݔ 全 ͳ 求数列的前，1ݔ n项和． 18. 如图，已知 平面 ACD，‸ 平面 ACD， 为等边三角形， 全 ‸ 全 F为，ݔ CD的中点． 1㌳求证：：：平面 BCE； ㌳求二面角ݔ ‸ 的余弦值的大小． 19. 携号转网，也称作号码携带、移机不改号，即无需改变自己的手机号码，就能转换运营商，并 享受其提供的各种服务．2019年 11月 27日，工信部宣布携号转网在全国范围正式启动．某运 营商为提质量保客户，从运营系统中选出 300名客户，对业务水平和服务水平的评价进行统计， 其中业务水平的满意率为 13 1䁪 ，服务水平的满意率为 ݔ 3 ，对业务水平和服务水平都满意的客户有 180 人． Ⅰ㌳完成下面 ݔ 列联表，并分析是否有ݔ .䁪的把握认为业务水平与服务水平有关； 对服务水平满意人数 对服务水平不满意人数 合计 对业务水平满意人数 对业务水平不满意人数 合计 Ⅱ㌳为进一步提高服务质量，在选出的对服务水平不满意的客户中，抽取 2名征求改进意见， 用 X表示对业务水平不满意的人数，求 X的分布列与期望； 附：ݔ 全 ͳ݀ ݔ ͳ ݀ ͳ ݀ ， 全 ͳ ݀． ݔ 香.1香 香.香䁪 香.香ݔ䁪 香.香1香 香.香香䁪 香.香香1 k 香6.ݔ 3.ͳ1 䁪.香ݔͳ 6.63䁪 . 1香.ݔ .香ݔ 已知椭圆 ‸ ሼ ݔ ͳݔ ݔ ݔ 全 1ͳ ㈠ ㈠ 香㌳的右准线方程为 ሼ 全 又离心率为，ݔ ݔ ݔ ，椭圆的左顶点为 A， 上顶点为 B，点 P为椭圆上异于 A、B任意一点． 1㌳求椭圆的方程； ㌳若直线ݔ BP与 x轴交于点 M，直线 AP与 y轴交于点 N，求证； 为定值． 21. 已知函数 ሼ㌳ 全 ͳሼ ሼݔ 1 集㌳． 1㌳若函数在点1䁥1㌳㌳处的切线与直线 ሼݔ 1 全 香平行，求实数 m的值； ㌳若对任意ݔ ሼ 1䁥ǡ㌳，都有 ሼ㌳ 香恒成立，求实数 m的取值范围． 22. 在极坐标系中，曲线1： 全 香：ݔ曲线，ݔ 全 3，点 1䁥㌳，以极点为原点，极轴为 x 轴正半轴建立直角坐标系． 1㌳求曲线1和ݔ的直角坐标方程； ㌳过点ݔ P的直线 l交1于点 A，B，交ݔ于点 Q，若 全 ，求的最大值． 23. 设函数 ሼ㌳ 全 lgሼ 1 ሼ ݔ ͳ㌳． 1㌳当 ͳ 全 䁪时，求函数 ሼ㌳的定义域； ㌳设ݔ ሼ㌳ 全 ሼ 1 ሼ ݔ ͳ，当 ሼ 䁥1െ时，ሼ㌳ݔ ሼ ͳ成立，求ݔ a的取值范围． 【答案与解析】 1.答案：D 解析： 本题考查集合的交并补运算，先求出集合 B的补集，再和集合 A取交集，画出数轴即可，注意求补 集时的边界问题． 解： 全 ሼሼ 或ݔ ሼ 䁪， 所以 ㌳ 全 ሼ1 ሼ ，ݔ 故选 D． 2.答案：A 解析： 本题主要考察复数的代数表示及其几何意义，属于基础题。 全 1 ͳ㌳ͳ ㌳ݔ 全 3ͳ ݔ ͳݔ㌳，依据题意复数 z在复平面内对应的点在第一象限，所以 3ͳ ㈠ 香 ݔ ͳݔ ㈠ 香 解得 香 ͳ 则实数，ݔ a取值范围是香䁥 。㌳ݔ 故选 A． 3.答案：C 解析：解：不等式 ሼݔ ሼݔ 香的解集是ሼሼ 香或 ሼ ㈠ ，ݔ 故 p为真命题， 在 中， ㈠ 是 ㈠ 的充要条件 故 q为真命题． 故 A，D错， 又 为真，故 B错． 故选 C． 本题考察了复合或、且、非㌳命题的判定，属于基础题． 4.答案：A 解析： 本题主要考查了等比数列的求和，属于基础题． 直接用等比数列的求和公式求解． 解：根据等比数列的前 n项和公式，可知䁪 全 ͳ11䁪㌳ 1 全 ㌳ݔ11 䁪െ ݔ11 全 31 ݔ ， 故选 A． 5.答案：B 解析： 本题考查双曲线的简单性质的应用，是基本知识的考查． 求出右焦点的坐标，渐近线的斜率，然后求解 a即可． 解：直线 全 ሼݔ ݔ 䁪经过双曲线的右焦点，可得 全 䁪， 双曲线 ሼݔ ͳݔ ݔ ݔ 全 1ͳ ㈠ 香䁥 ㈠ 香㌳的一条渐近线与过其右焦点的直线 全 ሼݔ ݔ 䁪平行， 可得 ͳ 全 ݔ又ͳ，ݔ ݔ 全 䁪，解得 ͳ 全 1，所以双曲线的实轴长为：2． 故选：B． 6.答案：C 解析： 本题主要考查了三视图的还原问题，关键是得到原几何体，与垂直关系的确定，属基础题． 本题只要画出原几何体，理清位置及数量关系，由勾股定理可得答案． 解：由三视图可知原几何体为三棱锥， 其中底面 为俯视图中的直角三角形，为直角， 其中 全 3， 全 ͳ， 全 䁪， 底面 ABC，且 全 ͳ， 由以上条件可知，为直角，最长的棱为 PC， 在直角三角形 PBC中，由勾股定理得， 全 ݔ ݔ 全 ͳݔ 䁪ݔ 全 ͳ1． 故选 C． 7.答案：C 解析： 本题主要考查三角函数的图象平移变换，属于基础题． 解：将函数 的图象向左平移 ͳ个单位得到 ሼ 的图象， 则 ． 故选 C． 8.答案：A 解析： 根据已知求出圆心到直线的距离 d，再根据 d与 r的大小关系即可判断直线与圆的位置关系． 本题考查点到直线的距离公式，直线与圆的位置关系等知识，属于基础题． 解：圆 C：ሼݔ ݔ ͳሼ 全 香可化为 ሼ ݔ㌳ݔ ݔ 全 ͳ． 圆心 䁥香㌳，半径ݔ 全 ．ݔ 圆心到直线 l：ሼ 3 全 香的距离为 ݀ 全 3ݔ ݔ1 全 1 ݔ1 1． ݀ ． 直线 l与圆 C相交． 故选：A． 9.答案：C 解析： 本题主要考查二项式定理的应用，二项展开式的通项，二项式系数的性质，属于基础题.由已知结合 二项式系数的性质逐一求得 a，ͳ1，ͳ3，ͳ䁪的值，则答案可求． 解：由已知根据二项展开式的通项可得： 1 ͳ䁪 全 香，得 ͳ 全 1． 且ͳ1 全 䁪ݔ 1 䁪ݔ 1 全 香，ͳ3ݔ 全 3䁪ݔ 3 3䁪ݔ 3 全 16香，ͳ䁪 全 䁪䁪ݔ 䁪 䁪䁪ݔ 䁪 全 6ͳ． ͳ ͳ1 ͳ3 ͳ䁪 全 1 香ݔ 16香 6ͳ 全 ．ͳ3ݔ 故选：C． 10.答案：B 解析：解：由题意，由正弦定理可得 外接圆的半径为 1 ݔ 3 1 ݔ 全 3， 平面 ABC， 全 ，ݔ 四面体 ABCD的外接球的半径为 1 3 全 ，ݔ 球 O的表面积为 ͳ ͳ 全 16． 故选：B． 由正弦定理可得 外接圆的半径，利用勾股定理可得四面体 ABCD的外接球的半径，即可求出 球 O的表面积． 本题考查球 O的表面积，考查学生的计算能力，确定四面体 ABCD的外接球的半径是关键． 11.答案：B 解析：解：因为函数 ሼ㌳有两个零点，故方程lgሼ 1㌳ 全 ͳሼ香 ͳ 1㌳有两个解ሼ1，ሼݔሼ1 ሼݔ㌳. 设函数 ሼ㌳ 全 lgሼ 1㌳，函数 ሼ㌳ 全 ͳሼ，则 ሼ㌳ 全 lgሼ 1㌳与 ሼ㌳ 全 ͳሼ的图象有两个交点， 由图象知，香 ሼ1 ݔ ሼݔ， 所以 lgሼ1 1㌳ 全 ͳሼ1，lgሼݔ 1㌳ 全 ͳሼݔ，因为 香 ͳ 1，所以ͳሼ1 ㈠ ͳሼݔ， 得 lgሼ1 1㌳ ㈠ lgሼݔ 1㌳，lgሼ1 1㌳ሼݔ 1㌳ 香，即ሼ1 1㌳ሼݔ 1㌳ 1，整理得，ሼ1ሼݔ ሼ1 ሼݔ． 故选：B． 因为函数 ሼ㌳有两个零点，故方程lgሼ 1㌳ 全 ͳሼ香 ͳ 1㌳有两个解ሼ1，ሼݔሼ1 ሼݔ㌳， 设函数 ሼ㌳ 全 lgሼ 1㌳，函数 ሼ㌳ 全 ͳሼ，则 ሼ㌳ 全 lgሼ 1㌳与 ሼ㌳ 全 ͳሼ的图象有两个交点， 作出两个函数的图象，进而求解； 考查绝对值函数的求解，转化法，指数函数对数函数图象的理解，属于中档题； 12.答案：B 解析：解：ሼ㌳ 全 1 ݔ1 ሼͳ 1 ݔ ͳሼݔ，̵ሼ㌳ 全 1 3 ሼ3 ͳሼ， ̵ሼ㌳在 R上是增函数， ሼ㌳ 全 ሼݔ ͳ 香在 R上恒成立， 即 ͳ ሼݔ，则 ͳ 香． 实数 a的取值范围是 ͳ 香． 故选：B． 求出原函数的导函数，二次求导后，由 ሼ㌳ 香在 R上恒成立可得实数 a的取值范围． 本题考查利用导数研究函数的单调性，熟记初等函数的求导公式是关键，是中档题． 13.答案：1 解析：解： ͳ ， ͳ 全 ݔ ሼݔ 全 香，解得 ሼ 全 1． 故答案为：1． 由ͳ ，可得ͳ 全 香，解出即可． 本题考查了向量垂直与数量积的关系，属于基础题． 14.答案：1 解析： 本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．利用平移确定目标 函数取得最优解的条件是解决本题的关键． 解：作出不等式组对应的平面区域如下图：黄色阴影部分㌳． 由 全 ሼ 得 全 ሼ ，平移直线 全 ሼ ， 由图象可知当直线 全 ሼ 经过点 B时，直线 全 ሼ 的截距最大，此时 z最大． 由 3ሼ 1 全 香 ሼ 全 ͳ ，得 ͳ䁥3ͳ 1 ， 即目标函数 全 ሼ 的最大值为 ͳͳ 1，又知目标函数 全 ሼ 的最大值为 5a ，则有 ͳͳ 1 全 䁪ͳ， 可得 ͳ 全 1． 故答案为 1 ． 15.答案： 1 3 解析：解：由题意可知 全 ，香ݔ1 全 1 ݔ 香ݔ1 全 3 3． 则 1 ݔ 全 1 3 31 全 1 3 3 1 1， 当1最大时， 1 ݔ 的最大，故只需求1最大值即可． 设 全 ሼ香 ሼ 6㌳，‸ 全 香 ，㌳ݔ 由余弦定理得 ݔ‸ 全 ሼݔ ݔ 香，即ݔሼ香1ݔ 全 ሼݔ ݔ ሼ， 从而 ሼݔ ሼ 全 3ሼ，即 ሼ 3.当且仅当 ሼ 全 全 3时等号成立． 1 全 1 ݔ ሼ 全 3 ͳ ሼ 3 ͳ 3． 则 1 ݔ 的最大值为 1 3 ． 故答案为： 1 3 ． 求得 全 3 3.又 1 ݔ 全 1 3 31 全 1 3 3 1 1，只需当1最大时， 1 ݔ 的最大，只需求1最大值即可． 本题考查三角形的面积计算，基本不等式的应用，考查了转化思想，属于中档题． 16.答案：3 解析： 本题考查直线与抛物线的位置关系的应用，考查运算求解能力．属于中档题． 设出直线方程，与抛物线方程联立，求出直线方程，转化求解即可． 解：抛物线 C：ݔ 全 ሼ的焦点为 ，䁥香㌳ݔ 直线 l过 F，设直线 l的方程为： 全 ሼ ，㌳ݔ 代入抛物线方程，可得：ݔሼݔ ͳݔ ㌳ሼ ͳݔ 全 香， 由 全 ݔ3 3 ，可得ሼ1 ሼݔ 全 ݔ3 3 ， 即： ͳݔ ݔ ͳ 全 ݔ3 3 ， 解得 全 3，不妨取 全 3， 解得ሼ1 全 6，则ሼݔ 全 ݔ 3 ， 因为 ㈠ ，所以 全 ሼ1 ݔ 全 ， 全 ሼݔ ݔ 全 3 ， 所以： 全 3 全 3． 故答案为：3． 17.答案：解：1㌳由已知 ， 可得： ， ， ， 即 ， 因为 ， 又因为 ， 所以 是以 1为首项，2为公比的等比数列． ㌳由1㌳得ݔ ， 即 ， 所以 ， 设 ，且前 项和为 ， 所以 ， ， 得： 1 ݔ 全 1 1 ݔ 1 ݔݔ 1 3ݔ 1 1ݔ ㌳ ݔ 全 1 1 ݔ 1 1 1ݔ ݔ11 ݔ 全 ݔ ݔ ݔ ， 所以 ， 因此 ． 解析：本题考查数列的递推关系、等比数列的判定以及错位相减法求和，属于中档题． 1㌳根据数列 ͳ 的递推公式利用待定系数法转换，即可证明 ͳ 是以 1为首项，2为公比的等比 数列． ㌳由1㌳可求得ݔ ͳ 的通项，从而得到 的通项，利用错位相减法得出 的表达式，从而求得． 18.答案：证明：1㌳设 全 ‸ 全 ݔ 全 ，ͳݔ 以 A为原点，AC，AB所在的直线分别作为 x轴、z轴，以过点 A在平面 ACD内和 AC垂直的直线 作为 y轴，建立如图所示的坐标系， 香䁥0，香㌳，ݔͳ䁥0，香㌳，香䁥0，ͳ㌳，ͳ䁥 3ͳ䁥香㌳，‸ͳ䁥 3ͳ䁥ݔͳ㌳． 为 CD的中点， 3ͳ ݔ 䁥 3ͳ ݔ 䁥香㌳， 全 3 ݔ ͳ䁥 3ͳ ݔ 䁥香㌳，‸ 全 ͳ䁥 3ͳ䁥ͳ㌳， 全 ，ͳ䁥0ݔ ͳ㌳， 全 1 ݔ ‸ ㌳， 设 CE的中点为 G，则 全 ， ：：，又 平面 BCE， 平面 BCE， ：：平面 BCE． 解：ݔ㌳设平面 BCE的一个法向量 全 ሼ䁥y，㌳， 则 ‸ 全 ͳሼ 3ͳ ͳ 全 香 全 ͳሼݔ ͳ 全 香 ，令 ሼ 全 1，得 全 1䁥 3䁥ݔ㌳． 设平面 BDE的一个法向量 全 䁥j，㌳， 全 ͳ䁥 3ͳ䁥 ͳ㌳， 则 ‸ 全 ͳ 3ͳ݆ ͳ 全 香 全 ͳ 3ͳ݆ ͳ 全 香 ，令 全 3，得 全 3䁥 1䁥香㌳． cos 䁥 ㈠全 全 6 ͳ ． 由图可知二面角 ‸ 为锐二面角， 故二面角 ‸ 的余弦值为 6 ͳ ． 解析：本题考查线面平行的证明，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的 位置关系等基础知识，考查运算求解能力，是中档题． 1㌳设 全 ‸ 全 ݔ 全 ͳ，以以ݔ A为原点，AC，AB所在的直线分别作为 x轴、z轴，以过点 A 在平面 ACD内和 AC垂直的直线作为 y轴，建立空间直角坐标系，利用向量法能证明 ：：平面 BCE． ㌳求出平面ݔ BCE的一个法向量和平面 BDE的一个法向量，利用向量法能求出二面角 ‸ 的 余弦值． 19.答案：解：Ⅰ㌳由题意知，对业务水平满意的有 3香香 13 1䁪 全 ，6香人ݔ 对服务水平满意的有 3香香 ݔ 3 全 ，香香人ݔ 对业务水平和服务水平都满意的客户有 180人， 从而得到如下 ݔ ：列联表ݔ 对服务水平满意人数对服务水平不满意人数合计 对业务水平满意人数 180 80 260 对业务水平不满意人数 20 20 40 合计 200 100 300 经计算得 ， 所以有 的把握认为业务水平满意与服务水平满意有关． Ⅱ㌳ 的可能值为 0，1，2． 则 ， ， ， X 0 1 2 P 316 ͳ䁪 16香 ͳ䁪 1 ͳ䁪 ． 解析：本题考查独立性检验以及离散型随机变量的分布列、数学期望和概率的求法，属于中档题． Ⅰ㌳求出列联表，然后直接代入公式即可求出结果； Ⅱ㌳ 的可能值为 ．分别求出概率即可求出分布列和数学期望.ݔ，0，1 20.答案：解：1㌳ 右准线方程为 ሼ 全 离心率为，ݔ ݔ ݔ ， 可得得ͳݔ 全 䁥ݔ ͳ 全 ݔ ݔ ， 又ͳݔ 全 ݔ ，ݔ 解得 ͳ 全 ，ݔ 全 1． 椭圆的方程为： ሼݔ ݔ ݔ 全 1． ㌳证明：由1㌳知ݔ ，䁥香㌳，香䁥1㌳ݔ 设 ሼ香䁥香㌳， 则ሼ香ݔ ݔ香ݔ 全 ，ݔ 当ሼ香 全 香时，香䁥香㌳，香䁥 1㌳， 全 ͳݔ 全 ݔ ．ݔ 当ሼ香 香时， 直线 PA的方程为： 全 香 ሼ香 ݔ ሼ ݔ ， 令 ሼ 全 香，得： 全 香ݔ ሼ香 ݔ ， 故： 全 1 香ݔ ሼ香 ݔ ，直线 PB的方程为： 全 香1 ሼ香 ሼ 1， 令 全 香，得：，ሼ 全 ሼ香 1香 ， 全 ݔ ሼ香 1香 ， 即 全 ሼ香 ݔ 香ݔ ݔ ሼ香 ݔ 香1 全 ሼ香 ݔݔݔ香ݔݔ ݔሼ香香ݔ ሼ香ͳ香ݔ ሼ香香ሼ香 香ݔ ݔ 全 ݔ ．为定值ݔ 综上所述， 为定值 ݔ ．ݔ 解析：本题考查了椭圆的标准方程，直线与椭圆的位置关系，属中档题． 1㌳结合椭圆的准线方程及离心率，求出 a和 b，即可得到椭圆的标准方程； ㌳写出直线方程，表示ݔ M与 N的坐标，求出 ，求解其为定值即可． 21.答案：解：1㌳由题知：̵ሼ㌳ 全 ͳ ሼ ሼ，函数ݔ ሼ㌳在 ሼ 全 1处的切线斜率为 2， 即̵1㌳ 全 即，ݔ ͳ ݔ 全 得，ݔ 全 1，经检验 全 1满足题意， 实数 m的值为 1． ㌳由题知：ͳሼݔ ሼݔ 1 香在 ሼ 1䁥ǡ㌳上恒成立， 即 ͳሼ1 ሼݔ 在 ሼ 1䁥ǡ㌳上恒成立． 令 ሼ㌳ 全 ͳሼ1 ሼݔ ，ሼ 1䁥ǡ㌳， 所以̵ሼ㌳ 全 1ͳሼ㌳ݔ ሼ3 ， 令̵ሼ㌳ ㈠ 香，则 1ሼ ǡ 1 ͳ； 令̵ሼ㌳ 香，则ǡ 1 ͳ ሼ ǡ． ሼ㌳在1䁥ǡ 1 ͳ㌳上单调递增，在ǡ 1 ͳ䁥ǡ㌳上单调递减． ሼ㌳ͳሼ 全 ǡ 1 ͳ㌳ 全 ݔ ǡ ǡ ， ݔ ǡ ǡ ． 故 m的取值范围是 ݔ ǡ ǡ 䁥 ㌳． 解析：本题主要考查了导数的几何意义，利用导数研究函数恒成立问题，是中档题． 1㌳求出函数的导数，根据切线斜率得到关于 m的方程，求解验证即可； ㌳问题转化为ݔ ͳሼ1 ሼݔ 在 ሼ 1䁥ǡ㌳上恒成立．令 ሼ㌳ 全 ͳሼ1 ሼݔ ，ሼ 1䁥ǡ㌳，利用导数结合函数的单 调性求解即可． 22.答案：解：1㌳曲线1： 全 ，ݔ 所以：曲线1的直角坐标方程为：ሼݔ ݔ ݔ 全 香； 曲线ݔ：香 全 3， 所以：曲线ݔ的直角坐标方程为：ሼ 全 3． ㌳的直角坐标为ݔ 1䁥香㌳， 设直线 l的倾斜角为，香 ݔ ㌳， 则直线 l的参数方程为： ሼ 全 1 ͳ香 全 ͳ ͳ为参数，香 ݔ ㌳ 代入1的直角坐标方程整理得， ͳݔ ݔ 香㌳ͳ 1 全 香， ͳ1 ͳݔ 全 ݔ 香㌳ 直线 l的参数方程与 ሼ 全 3联立解得， ͳ3 全 ͳ cos ， 由 t的几何意义可知， 全 ݔ 香㌳ 全 全 ͳ cos ， 整理得， ͳ 全 ݔ 香㌳香 全 ݔ 香ݔ 1 全 ݔsinݔ ͳ ㌳ 1， 由 香 ，ݔ ͳ ݔ ͳ 䁪 ͳ ， 所以， 当 ݔ ͳ 全 即，ݔ 全 时， 有最大值 1 ͳ ݔ 1㌳． 解析：1㌳直接利用转换关系，把参数方程和极坐标方程与直角坐标方程进行转化． ．㌳利用一元二次方程根与系数的关系，利用三角函数的变换求出结果ݔ 本题考查的知识要点：参数方程和极坐标方程与直角坐标方程的转化，一元二次方程根与系数的关 系的应用，三角函数的关系式的恒等变换． 23.答案：解：1㌳当 ͳ 全 䁪时，要使函数 ሼ㌳有意义，需满足ሼ ሼ ݔ 䁪 ㈠ 香， ሼ 1 ሼ ݔ 䁪 ㈠ 香 ሼ 䁥ݔ ሼݔ 6 ㈠ 香䁥或 ݔ ሼ 1䁥 ݔ 香䁥 或 ሼ 1䁥 ሼݔ ͳ ㈠ 香䁥 ሼ 3或 ሼ ㈠ ．ݔ 所以函数的定义域为 䁥 3㌳ 䁥ݔ ㌳． ㌳当ݔ ሼ 䁥1െ时，ሼݔ 1 ሼ ݔ ͳ ሼ ，ͳ成立ݔ 即 ͳ 3 ሼ ͳ成立，所以ݔ ͳ 3且 ͳ 3 ሼ ͳݔ ͳ 3， 可得 ሼ 3 1 ͳ ሼ 3，而 ሼ 䁥1െ，ሼݔ 3 1 䁪 3 䁥 ݔ 3 െ，ሼ 3 1䁥ͳെ， 所以 a的取值范围是 ݔ 3 䁥1െ． 解析：本题主要考查的是绝对值不等式的解法及不等式恒成立问题，属于中档题． 1㌳转化为解不等式ሼ ሼ ݔ 䁪 ㈠ 香问题，再分段讨论去绝对值解不等式即可； ㌳当ݔ ሼ 䁥1െ时，先对ሼݔ 1 ሼ ݔ ͳ ሼ ͳ转化为ݔ ͳ 3 ሼ ．ͳ，再求解即可ݔ