2014南平5月份质检文数试卷 11页

福建省南平市2014年普通高中毕业班质量检查 数学（文）试题 本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)，第Ⅱ卷第21题为选考题，其他题为必考题．本试卷共6页．满分150分．考试时间120分钟．‎ 注意事项：‎ ‎ 1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．‎ ‎ 2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．‎ ‎ 3．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0．5毫米的黑色中性(签字)笔或碳素笔书写，字体工整、笔迹清楚．‎ ‎ 4．做选考题时，考生按照题目要求作答，并用213铅笔在答题卡上把所选题目对应的题号涂黑．‎ ‎ 5．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．‎ 参考公式：‎ 第I卷 (选择题共50分)‎ 一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．‎ ‎ ‎ ‎2．已知复数z满足为虚数单位，则复数z等于 ‎ A． B． C． D．‎ ‎3．已知则x等于 ‎ A．—1 B．‎0 ‎C．2 D．6‎ ‎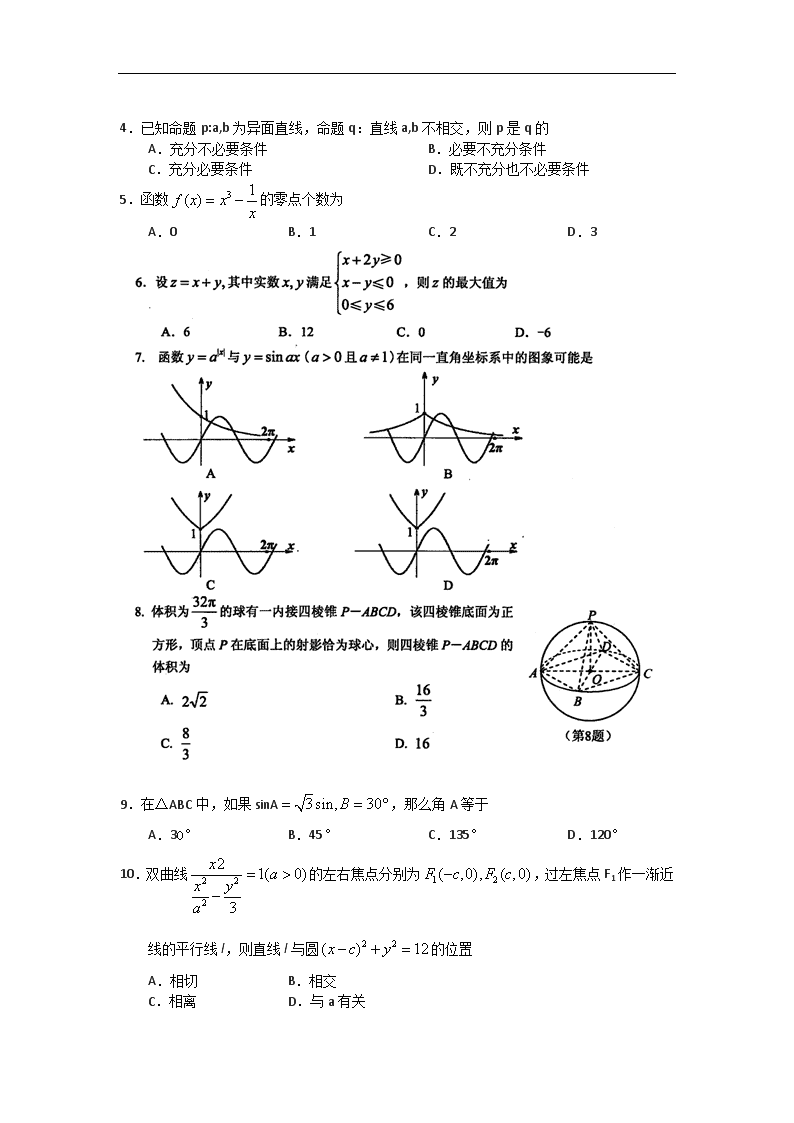4．已知命题p:a,b为异面直线，命题q：直线a,b不相交，则p是q的 ‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充分必要条件 D．既不充分也不必要条件 ‎5．函数的零点个数为 ‎ A．0 B．‎1 ‎C．2 D．3‎ ‎9．在△ABC中，如果sinA，那么角A等于 ‎ A．30° B．45° C．135° D．120°‎ ‎10．双曲线的左右焦点分别为，过左焦点F1作一渐近线的平行线l，则直线l与圆的位置 ‎ A．相切 B．相交 ‎ ‎ C．相离 D．与a有关 ‎ A．1 B．‎2 ‎C．3 D．4‎ 第II卷（非选择题，共90分）‎ 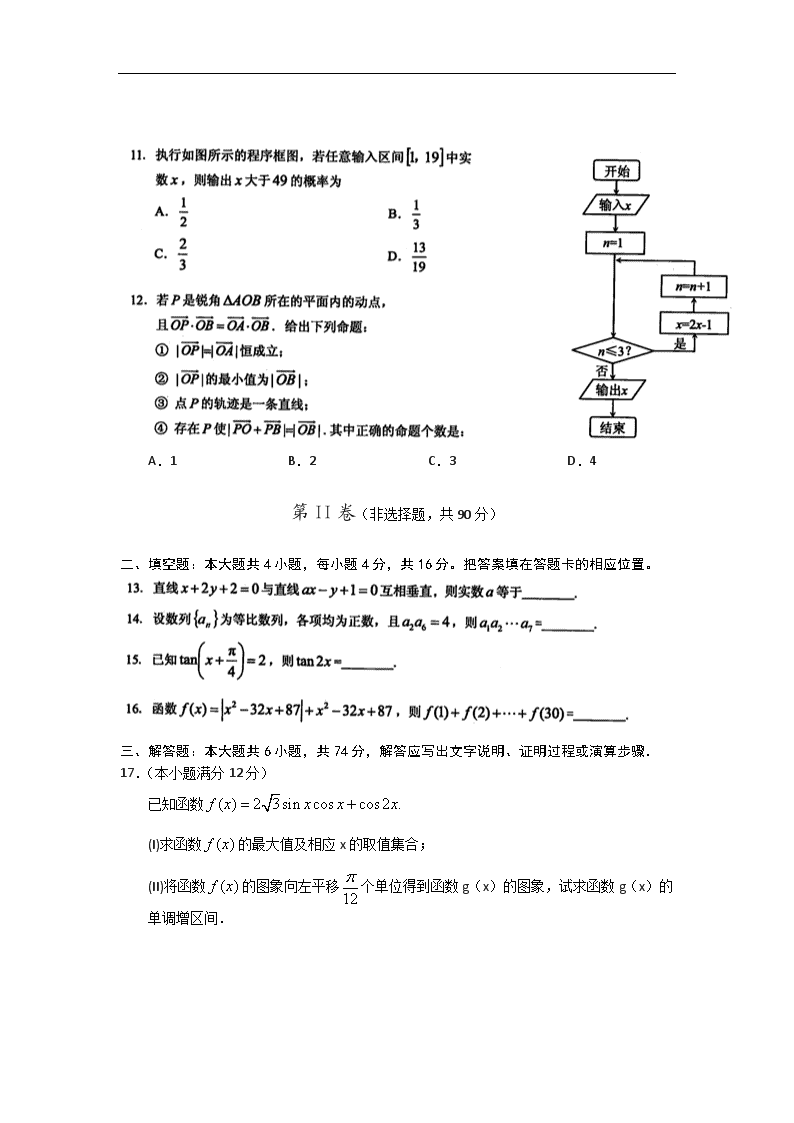二、填空题：本大题共4小题，每小题4分，共16分。把答案填在答题卡的相应位置。‎ 三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（本小题满分12分）‎ ‎ 已知函数 ‎ (I)求函数的最大值及相应x的取值集合；‎ ‎ (II)将函数的图象向左平移个单位得到函数g（x）的图象，试求函数g（x）的 ‎ 单调增区间．‎ ‎18．（本小题满分12分）‎ ‎ 某中学从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50)，[50，60)，…，[90，100]后得到如图的频率分布直方图．‎ ‎ (I)求图中实数口的值：‎ ‎ (II)若该校高一年级共有学生640人，‎ ‎ 试估计该校高一年级期中考试数学 ‎ 成绩不低于60分的人数；‎ ‎ (Ⅲ)若从样本中数学成绩在[40，50)与 ‎ [90，100]的所有学生中随机选取两 ‎ 名学生，求这两名学生的数学成绩之 ‎ 差的绝对值不大于10的概率．‎ ‎19.（本小题满分12分）‎ ‎ ‎ ‎20．（本小题满分12分）‎ ‎21．（本小题满分12分）‎ ‎ 已知{}为等差数列，Sn为其前n项和，且a3 =9，S6=60.‎ ‎ (I)求数列{}的通项公式；‎ ‎ ‎ ‎22.（本小题满分14分）‎ ‎2014年南平市高中毕业班适应性考试 文科数学试题参考答案及评分标准 说明：‎ ‎ 一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．‎ ‎ 二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．‎ ‎ 三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．‎ 四、只给整数分数．选择题和填空题不给中间分．‎ 一、选择题：本题考查基础知识和基本运算，每小题5分，满分60分.‎ ‎1. C； 2. A； 3. C； 4.A； 5. C； 6. B； 7. D； 8. B； 9. D； 10. A； 11. C； 12. B.‎ 二、填空题：本题考查基础知识和基本运算，每小题4分，满分16分.‎ ‎13．2； 14．128； 15．； 16．220.‎ 三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤．‎ ‎17．解：（Ⅰ）…………2分 ‎…………3分 ‎∴当时，…………5分 当取最大值时，…………6分 ‎（Ⅱ）依题意…………9分 ‎…………10分 ‎…………11分 故的单调增区间为…………12分 ‎18．解：（Ⅰ）由于图中所有小矩形的面积之和等于1，‎ 所以．…………2分 解得．…………3分 ‎（Ⅱ）成绩不低于60分的频率为．…………5分 由于该校高一年级共有学生640人，利用样本估计总体的思想，可估计该校高一年级 数学成绩不低于60分的人数约为人．…………7分 ‎（Ⅲ）成绩在分数段内的人数为人，分别记为，………8分 成绩在分数段内的人数为人，分别记为，，，……9分 若从数学成绩在与两个分数段内的学生中随机选取两名学生，则所有的基本事件有：，，，，，，，，，，，，，， 共15种 ‎…………10分 如果两名学生的数学成绩都在分数段内或都在分数段内，那么这两名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在分数段内，另一个成绩在分数段内，那么这两名学生的数学成绩之差的绝对值一定大于10．‎ 记“这两名学生的数学成绩之差的绝对值不大于‎10”‎为事件，则事件包含的基本事件有：‎ ‎，，，，，，共7种………11分 所以所求概率为．…………12分 ‎19．解：（I）由题意知 解得…………3分 由得b=2…………4分 故椭圆方程为…………5分 ‎（II）点A与点B关于轴对称，设、…………6分 由于点A在椭圆上，‎ 由已知有…………7分 则…………9分 由于0，故当时，取得最小值为…………10分 当时，，‎ 又点A在抛物线上，代入抛物线方程得…………11分 ‎∴抛物线方程为…………12分 ‎20. 解：（Ⅰ）几何体正视图面积即直角梯形PDCE的面积（此处没证明不扣分）……1分 F M N ‎ ‎ E ‎ ‎ P ‎ ‎ D ‎ ‎ C ‎ ‎ B A ‎ ‎ ‎∴S=…………3分 ‎（Ⅱ）取PD中点F，连接FC、FA，则CF∥PE，‎ ‎∴∠FCA为异面直线与所成角…………4分 ‎∵PD⊥平面ABCD，∴PD⊥AD，PD⊥DC，‎ ‎∴AF＝CF=，又AC＝…………5分 ‎∴在△FCA中cos∠FCA==‎ ‎ …………7分 即异面直线与所成角的余弦值为…………8分 ‎（Ⅲ）面PBD⊥面PBE…………9分 证明如下：‎ 取PB中点M，连接EM、MN，则MN∥PD且MN＝PD 又EC∥PD且EC＝PD，∴MN∥EC且MN＝EC，‎ ‎∴M NCE为平行四边形，∴EM∥CN. …………10分 ‎∵PD⊥面ABCD，∴PD⊥CN，又在正方形中ABCD中CN⊥BD，PD∩BD=D，‎ ‎∴CN⊥面PBD，∴EM⊥面PBD. …………11分 ‎∵EM面PBE，∴面PBE⊥面PBD. …………12分 ‎21. 解：（I）由已知得 ，…………2分 解得 …………4分 ‎（II）…………5分 是以4为首项2为公比的等比数列…………6分 ‎…………7分 ‎∴…………8分 ‎（Ⅲ）设…，则当≥2且时，‎ ‎…………9分 ‎=＞1.‎ 所以，即当增大时，也增大．……………10分 要使≤…对≥2且恒成立，‎ 只需即可．…………11分 ‎，即，所以实数的最大值为6．…………12分 ‎22. 解：（Ⅰ）由题意知， ．……………2分 ‎∴函数在点处的切线斜率 ……………3分 ‎∴切线方程为，即 ……………4分 ‎（Ⅱ）令得 ……………5分 ‎① 当时，在上，单调递增，‎ ‎② 当时，在上，单调递减，在上，‎ 单调递增，∴‎ ‎③ 当时，在上，单调递减，‎ ‎……………8分（每个讨论1分）‎ ‎∴……………9分 ‎（Ⅲ）函数在上不存在同步偏移区间 ……………10分 证明如下：‎ 假设函数存在同步偏移区间， ‎ 则……………11分 ‎∵时， ，∴为增函数，∴ ‎ 即方程有两个大于的相异实根…………12分 设，则 ‎∵，，∴在上单调递增. …………13分 ‎∴在区间上至多有一个零点与方程有两个大于的相异实根矛盾 ‎∴假设不成立，即在上不存在同步偏移区间. …………14分